3081
Phase-based T2 mapping using RF phase-modulated dual echo steady-state (DESS) imaging1Radiology, University of Wisconsin-Madison, Madison, WI, United States, 2Medical Physics, University of Wisconsin-Madison, Madison, WI, United States, 3Biomedical Engineering, University of Wisconsin-Madison, Madison, WI, United States, 4Medicine, University of Wisconsin-Madison, Madison, WI, United States, 5Emergency Medicine, University of Wisconsin-Madison, Madison, WI, United States
Synopsis
A novel T2 mapping method is proposed using RF-phase modulated dual echo steady-state sequence (DESS). T2 information is encoded into the phase of the DESS signals by using a small RF phase increment. T2 value is estimated from the phase difference between the FISP and PSIF signal of the DESS acquisition. Phantom studies demonstrated that estimated T2 using the proposed method agrees closely with spin-echo-based T2 mapping, and volunteer studies demonstrate the feasibility of the proposed method in vivo. These results suggested that the proposed method enables fast and three-dimensional T2 mapping with a single acquisition.
INTRODUCTION
Quantitative T2 mapping is gaining attention as a promising approach for the diagnosis and evaluation of various diseases. The Carr-Purcell-Meiboom-Gill sequence is the most commonly used approach for determining quantifying T2. Other approaches to T2 mapping include the use of T2-prep(1) and balanced steady-state free precession sequence is used in the myocardium(2). The magnitude signal from dual echo steady-state (DESS), and triple echo steady-state sequences have also been proposed for rapid T2 mapping(3)(4).Recently, a phase-based T2 mapping method that encodes T2 into phase of RF phase modulated gradient echo signal has been proposed and demonstrated (5). Despite rapid T2 mapping using the phase-based approach, two-pass imaging is required to subtract background phase. This doubles acquisition time and can result in misregistration between the two separate acquisitions.
In this study, we propose a novel phase-based T2 mapping using a multi-echo DESS with RF phase modulation. The feasibility in phantom and volunteer studies is demonstrated.
THEORY
We adopted Sobol's approach to explain the signal mechanism of the DESS signal with RF phase modulation (6). The RF phase modulation was performed by incrementing the RF phase ($$$\phi$$$) quadratically such that $$$\phi (n) = \phi (n-1) + n \theta$$$, where $$$\theta$$$ is the RF phase increment. The signal FISP (S+) and PSIF (S-) signals with RF pulse with flip angle (FA) of α, and a repetition time of TR can be expressed as$$S^+ = \beta (\eta e^{-\frac{TR}{T2}} + i [\eta^2 - \epsilon (e^{-\frac{TR}{T2}}-\epsilon)] )$$
$$S^- = \beta [\eta + i (e^{-\frac{TR}{T2}} - \eta)]$$
where $$$\beta$$$, $$$\epsilon$$$ and $$$\eta$$$ are real coefficients, determined by recursive calculation depending on T1, T2, TR, α, and θ (6). The phase difference $$$\Phi$$$ between S+ and S- is defined as
$$\Phi = arctan(\frac{S^+}{S^-})$$
These equations reveal that using small RF phase increments (θ) that the measured phase ($$$\Phi$$$) is sensitive to T2, but relatively insensitive to T1 for long T1 (> 1000 ms). Hence, Eq. 1-3 enables phase-based T2 mapping using the phase difference between the S+ and S-.
METHODS
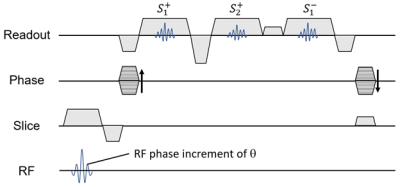
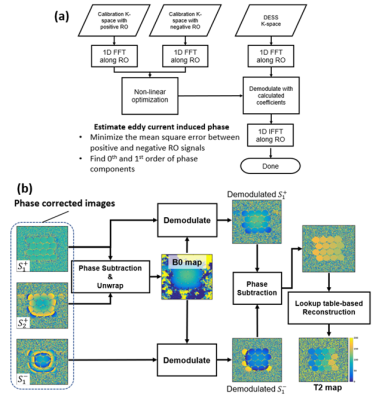
A three-echo DESS sequence shown in Figure 1 was developed. RF excitation was performed with quadratic phase modulation of θ. Acquisitions consist of two FISP echoes ($$$S^+_1$$$ and $$$S^+_2$$$) followed by PSIF echo ($$$S^-_1$$$). Calibration acquisitions were incorporated into the acquisition.- Phase errors induced by eddy current of k-space was are corrected using calibration acquisitions consisting of positive and negative readouts. The calibration algorithm is explained in Figure 2a.
- B0 demodulation of $$$S^+_1$$$ and $$$S^+_2$$$ was is performed to remove the off-resonance phase components of these echoes. A B0 map was is calculated from the phase difference.
- A lookup table (LUT) for phase-based T2 estimation was is used. The LUT was is calculated using equations 1-3 with an assumption of T1 of 1000 ms. The estimation of T2 was is performed by matching the phase difference of $$$S^+_1$$$ and $$$S^-_1$$$, and with the LUT.
RESULTS
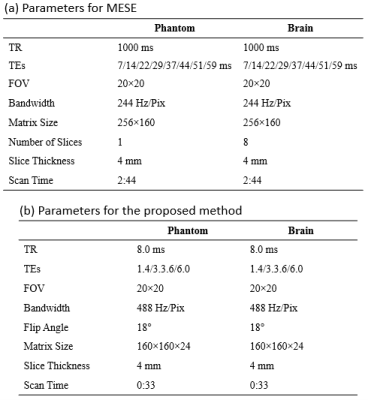
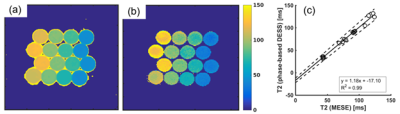
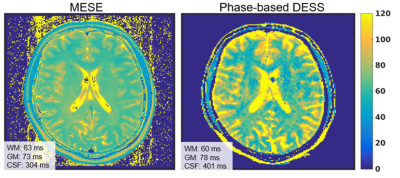
T2 maps of the phantom measured using the proposed method is shown in Figure 3a. T2 values agreed well (R2 = 0.99) with those measured using MESE, although slight overestimation of the proposed method was observed, as shown in Figure 3b. The slopes of the linear regression of the plot were 1.18 (95% CI = 1.12 to 1.24) and -17.1 (95% CI = -11.9 to -22.3).Figure 4 shows the T2 maps acquired using the MESE and proposed method. T2 values of white matter, gray matter, and CSF estimated using the proposed method were 60 (±11), 78 (±9.7), and 401 (±186) ms, while those using MESE were 62 (±2.5), 73 (±2.8), and 354 (±70).
DISCUSSION
In this study, we developed and demonstrated a novel T2 mapping method using a proposed RF phase-modulated DESS acquisition strategy. T2 was estimated from the phase difference of FISP and PSIF signals using the lookup table approach. Phantom and in vivo studies demonstrate the feasibility of the proposed method to enable fast three-dimensional T2 mapping.The proposed method requires a single acquisition, which enables faster T2 mapping without the potential for misregistration between two separate acquisitions. The majority of previously described T2 mapping methods require the use of multiple acquisitions. Conventional DESS-based T2 enables T2 mapping with one acquisition. However, it utilizes magnitude information for an estimation, which may be biased by T2*. On the other hand, since the proposed phase-based method does not depend on T2*.
A major limitation of the proposed method is that T2 may be bias by T1 and B1+, although it has been shown that phase-based T2 mapping is insensitive to them(5). In addition, the unbalanced readout gradient used in our method may lead to motion artifacts.
Conclusion
A new phase-based T2 mapping method using a multi-echo DESS was proposed. Phantom and volunteer studies suggested the proposed method may enable fast and reliable 3D T2 mapping.Acknowledgements
We wish to acknowledge support from the UW-Madison Department of Radiology, UW Institute for Clinical and Translational Research, and the Clinical and Translational Science Award of the NCATS/NIH. Further, we wish to acknowledge GE Healthcare who provides research support to the University of Wisconsin. Finally, Dr. Reeder is a Romnes Faculty Fellow, and has received an award provided by the University of Wisconsin-Madison Office of the Vice Chancellor for Research and Graduate Education with funding from the Wisconsin Alumni Research Foundation.References
1. Brittain JH, Hu BS, Wright GA, Meyer CH, Macovski A, Nishimura DG. Coronary angiography with magnetization‐prepared T2 contrast. Magnetic resonance in medicine 1995;33(5):689-696.
2. Huang TY, Liu YJ, Stemmer A, Poncelet BP. T2 measurement of the human myocardium using a T2‐prepared transient‐state TrueFISP sequence. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 2007;57(5):960-966.
3. Dregely I, Margolis DA, Sung K, Zhou Z, Rangwala N, Raman SS, Wu HH. Rapid quantitative T2 mapping of the prostate using three‐dimensional dual echo steady state MRI at 3T. Magnetic Resonance in Medicine 2016;76(6):1720-1729.
4. Sveinsson B, Chaudhari A, Gold G, Hargreaves B. A simple analytic method for estimating T2 in the knee from DESS. Magnetic resonance imaging 2017;38:63-70.
5. Wang X, Hernando D, Reeder SB. Phase‐based T2 mapping with gradient echo imaging. Magnetic Resonance in Medicine 2019.
6. Sobol WT, Gauntt DM. On the stationary states in gradient echo imaging. Journal of Magnetic Resonance Imaging 1996;6(2):384-398.
Figures