Introduction

Quantitative T₂ mapping is usually time consuming and sensitive to subject motion as it is dependent on repeated sampling with different contrast weighting information^1,2, which makes it difficult for dynamic imaging. Overlapping-echo detachment (OLED) planar imaging^3-5, proposed by our group, has been successfully applied in single-shot quantitative T₂ mapping with high accuracy, which tremendously improves the acquisition efficiency. However, the effect of motion during the OLED acquisition has not been fully investigated, especially when the parallel imaging technique^6,7 is applied. Herein, we combine OLED imaging with parallel acquisition and motion correction, to achieve fast quantification of T₂ in severe head motion. Meanwhile, we developed a synthetic-data-driven learning (SDDL) approach based on forward model for reconstruction of T₂ maps by generating simulated training data for different learning tasks to solve the problem of imperfect or insufficient data.

Methods

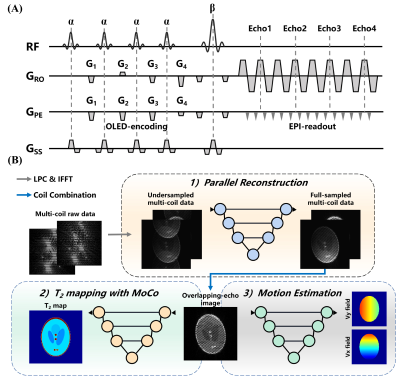
Pulse sequence: Figure 1A shows the sequence diagram of OLED acquisition. The four excitation pulses with a same flip angle α followed by refocusing pulse with a flip angle of β. The echo-shifting gradients G₁, G₂, G₃ and G₄ are used to shift the four echoes from the k-space center. Therefore, four echo signals were obtained with different evolution time at the same k-space data collection.
Experiments: In vivo data were acquired from healthy volunteers, on a whole-body MRI system at 3T with a 20-channel head coil (MAGNETOM Prisma, Siemens Health care, Erlangen, Germany). Participants were instructed for three scans: (1) reference scan, (2) no head motion scan, and (3) continuous motion scan. The acquisition parameters were as follows: field of view = 22×22 cm², voxel size = 1.72×1.72 mm², slice thickness = 3 mm, TR = 8000 ms, and slice number = 21. A GRAPPA acceleration rate of 2 was used to accelerate the acquisition. The pulse sequence and parameters used in simulation were the same as those used in experiments.
Parallel reconstruction: The proposed calibrationless parallel reconstruction approach is shown in Figure 1B. A U-Net was used to recover the multi-coil full-sampled images from undersampled images after navigator-based linear phase correction. Figure 2A shows the synthesis workflow of data for network training, which relays on the forward operator P=F^-1ΦFCB of parallel imaging, F is the Fourier operator, C applies coil sensitivities, B is the Bloch simulation and Φ is the sampling pattern. The coil sensitivity maps used in training phase were generated by ESPIRiT algorithm⁸ from several ACS data collected offline. ACS data is not needed in testing phase.
T₂ mapping with motion correction and estimation: Convolutional neural network has shown the capability of nonlinear mapping from overlapping-echo image to corresponding T₂ mapping.^4,5 To reduce the negative impact of subject movement, rigid motion was considered in this study. The forward operator E=F^-1BT_vR_θ of rigid motion is shows in Figure 2B, in which T_v and R_θ are translation operator and rotation operator, respectively. The phase accumulation due to motion during data acquisition can be represented by:
$$Δ\phi(\mathbf{r})= \gamma\left[\left(x-x'\right)\cdot G_{x}\left(t\right)+\left(y-y'\right)\cdot G_{y}\left(t\right)+\left(z-z'\right)\cdot G_{z}\left(t\right)\right]\cdot t $$
In which, γ is the gyromagnetic ratio, G(t) is the linear gradient field, x', y' and z' are transformed by motion matrix:
$$\begin{bmatrix}x' \\y' \\z'\end{bmatrix}=T_{v}R_{\theta}\begin{bmatrix}x \\y \\z\end{bmatrix}$$
Over 20,000 training samples with size of 256×256 were employed for network training, among which around 15,000 samples were simulated with motion and 5,000 samples without motion.

Results

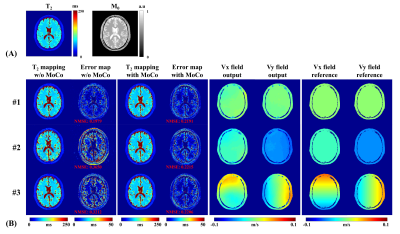
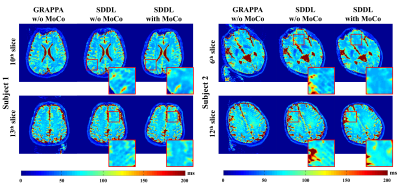
Figure 3 shows the results of numerical brain with/without rigid motion. The reconstructed T₂ maps and motion fields are very close to the corresponding references. The normalized mean squared error (NMSE) of all pixels (excluding the regions of the background and cerebrospinal fluid) between T₂ maps and reference are all reduced with motion correction in the presence of simulated motion. The results of simulation experiments show strong robustness to translational motion and rotational motion.
Figure 4 illustrates the results of in vivo experiments from two subjects. The GRAPPA cases suffer from ghosting artifacts, while motion artifacts are similar to those observed in the simulations before the correction. The proposed parallel reconstruction method reduces ghost artifacts and the motion correction method eliminates motion artifacts.
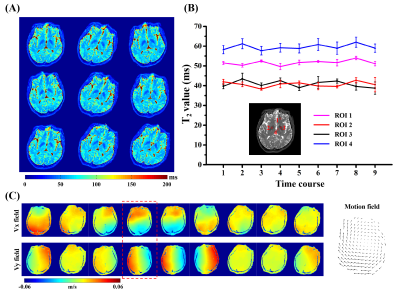
Figure 5 illustrates the results of T₂ maps and motion estimation from a continuous motion scan. The scan time is 125 ms per slice and 9 measurements were applied. As shown in Figure 5A, the T₂ maps scanned in different time courses maintain high consistency after coregistration, while there is slightly different distortion caused by altered inhomogeneous field under motion. Figure 5B shows that the T₂ values calculated from four regions of interest (ROIs) are quite consistent. The results of corresponding motion vector field are given in Figure 5C.

Discussion and conclusion

The proposed SDDL-based method shows excellent performance against motion artifacts in both simulation and in vivo human brain experiments. The combination of calibrationless parallel reconstruction and motion correction provides ghost-free T₂ maps in the presence of severe head motion. This method makes quantitative T₂ mapping applicable to patients who cannot keep motionless during MRI scan, such as elderly people, children or populations that suffer from epilepsy. Future work includes refinement of motion estimation, correction of non-rigid motion and more parametric mapping.

Acknowledgements

This work was supported by the National Natural Science Foundation of China under grant numbers 81671674, 11775184 and 82071913, and Leading (Key) Project of Fujian Province, 2019Y0001.