Introduction

Sodium nuclei yield the second largest in vivo MRI signal and can be used to image the function of excitable tissues in humans. In contrast to hydrogen nuclei in tissue, sodium nuclei have much faster relaxation times, which severely hampers data acquisition and image reconstruction. Efficient k-space sampling geometries (twisted projection imaging) are the preferred means to acquire sodium images in adequate imaging times. In this setting, signal decay due to fast transverse relaxation during the readout results in loss of high frequency information and a concomitant exacerbation of partial voluming. This k-space signal decay during the readout can be incorporated into the forward model of an iterative reconstruction algorithm using a time and position dependent decay function. The resulting reconstruction problem is, however, very ill-posed - especially if high frequencies are heavily attenuated or suffering from much lower SNR. To regularize the algorithm, anatomical priors can be used. In this work, we introduce and demonstrate a framework for iterative sodium MR reconstruction, which models the signal decay and jointly estimates the transverse sodium magnetization and the relaxation time in every voxel. The reconstruction is guided with anatomical (structural) information from a high resolution hydrogen MR image, using Bowsher's method [1].

Theory

In this work, we model the expected acquired signal in k-space as
$$\bar{s}[f,d](k) = \int_V f(x) c(x) d\left(x,t(k)\right) e^{-i 2 \pi \langle k,x\rangle} dx, $$
where $$$f$$$ is the transverse sodium magnetization to be reconstructed, $$$c$$$ is the coil sensitivity, $$$d$$$ is spatially dependent signal decay, and $$$t(k)$$$ is the readout time corresponding to a given k-space sample.

We approximate the signal decay using a mono-exponential model
$$d\left(x,t(k)\right) = e^{-\frac{t(k)}{T^*_{2}(x)}} = \Gamma (x) ^ \frac{t(k)}{T_E},$$
with
$$\Gamma (x) = e^{-\frac{T_E}{T^*_{2}(x)}},$$
where $$$T_E$$$ is the echo time of the 2nd echo, leading to the joint reconstruction problem for dual echo Na MR data
$$\text{argmin}_{f,\Gamma} \underbrace{||s_1 - \bar{s}_1[f,\Gamma]||_2^2}_\text{data fidelity 1st echo} + \underbrace{||s_2 - \bar{s}_2[\Gamma f,\Gamma]||_2^2}_\text{data fidelity 2nd echo} + \underbrace{\beta _f \left( R(\Re f) + R(\Im f) \right)+ \beta_\Gamma \, R(\Gamma)}_\text{regularization} \ ,$$
where $$$s_1$$$ and $$$s_2$$$ are the acquired k-space data of the first and second echo and $$$\Re f$$$ and $$$\Im f$$$ denote the real and imaginary part of $$$f$$$.
In this work, we use the symmetric Bowsher prior [1] to incorporate anatomical (structural) regularization on f and Γ where structural information is obtained from a high resolution hydrogen T1 MR image.

Methods

The proposed reconstruction framework was studied using 3D simulated and real dual echo data. Simulated data were generated based on the segmented brain-web phantom including realistic Na contrasts and T2* decay times and a realistic dual-echo readout with echo times of 0ms and 5ms and a readout time of ca 40ms. Stand-alone features in the Na, Γ, and anatomical prior image were added to study the transfer of non- shared structures. All reconstructions were done in 128x128x128 voxel grid. The image quality was analyzed in terms of regional bias and noise and compared to standard (filtered) inverse FFTs of the data using 25 noise realizations and different levels of regularization β_f while keeping β_Γ = 0.3 constant. Alternating L-BFGS-B updates [2] were used to solve the non-convex optimization problem. Experimental, dual echo, data from a brain tumor patient were acquired on a 3T Siemens MR using a dedicated eight-channel, dual-tuned, head coil. These data were reconstructed using the same framework and coil sensitivities estimated using a sum of squares image from all channels.

Results

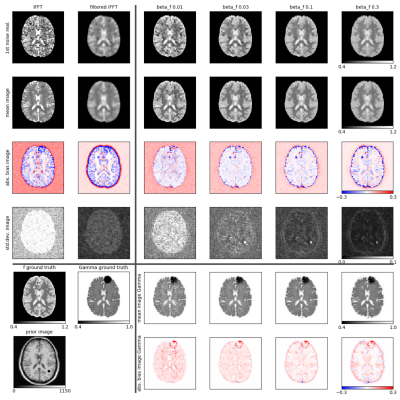
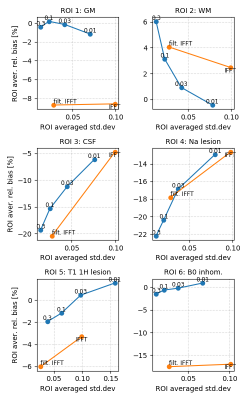
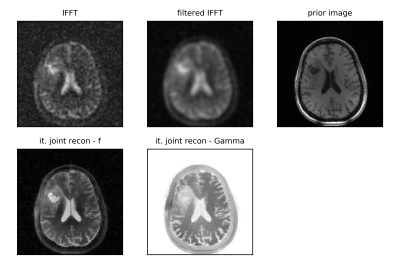
Figure 1 shows reconstructions of one noise realization, as well as mean, bias and standard deviation images for 25 noise realizations of the simulated data for our proposed joint iterative reconstruction framework for different levels of anatomical regularization in comparison to unfiltered and filtered inverse Fourier transforms of the data. Moreover, bias versus noise curves of 6 different regions are shown in Fig. 2. Figure 3 displays the reconstruction results of the patient brain tumor data set for one level of regularization.

Discussion

The results obtained from simulated data shown in Figs. 1 and 2 demonstrate that our proposed iterative joint reconstructions using anatomical regularization leads to superior bias-noise characteristics in regions where gradients (edges) are shared between the sodium and prior image. Especially in grey matter, the bias is strongly reduced. The anatomical regularization in combination with signal decay modeling and estimation allows to suppress noise while preserving anatomical detail at the same time. Transfer of non-shared gradients from the anatomical prior image into the sodium image is a potential source of bias that must be carefully controlled. This source of bias does not appear to compromise the gains obtained during experimental acquisitions. More experimental data and/or the use of non-anatomical priors in tandem with our proposed approach can be used to ascertain these effects.

Conclusion

Our proposed iterative joint reconstruction framework including anatomical regularization allows to suppress noise while preserving anatomical detail in reconstructions of dual echo sodium data. Moreover, it also allows to directly estimate a voxel-wise mono-exponential T2* decay time.

Acknowledgements

Supported in part by PHS grants P41 EB017183-01 and R01NS113517.