3052
Fast-Sweep Frequency-Modulated SSFP: Boosting Sensitivity for 3D Joint T1/T2 Mapping1Institute for Diagnostic and Interventional Radiology, University Medical Center Göttingen, Goettingen, Germany, 2DZHK (German Centre for Cardiovascular Research), Partner Site Göttingen, Germany, Goettingen, Germany, 3Campus Institute Data Science (CIDAS), University of Göttingen, Göttingen, Germany, Goettingen, Germany
Synopsis
Sensitivity to T1 and T2 in frequency-modulated SSFP sequences can be increased by choosing a higher modulation speed without prolonging the repetition time. In this work, we assess the boost in sensitivity by Cramér-Rao-bound analysis, combine the sequence with stack-of-stars sampling and subspace-constrained reconstruction, and demonstrate joint T1/T2/B1/off-resonance mapping in phantom and in vivo study. The results render fast-sweep frequency-modulated SSFP an excellent candidate for comprehensive 3D multi-parametric mapping.
INTRODUCTION
Recently, phase-cycled bSSFP methods were proposed to achieve robust joint T1/T2 mapping [1, 2]. These methods acquire a set of bSSFP images at different transmitter frequencies to jointly estimate parameter maps and off-resonance distribution. An alternative to the subsequent preparation of different steady states is given by frequency-modulated SSFP (fmSSFP), a bSSFP sequence in which the transmitter frequency is modulated slowly but continuously [3]. While a very slow modulation ("quasistatic") simply sweeps through the classic bSSFP spectrum, a faster modulation results in a different signal response.In this work, we investigate the increased sensitivity of the "fast-sweep" fmSSFP, combine this novel sequence with a stack-of-stars sampling scheme, and demonstrate joint T1/T2/B1/off-resonance mapping in phantom and in vivo.
THEORY
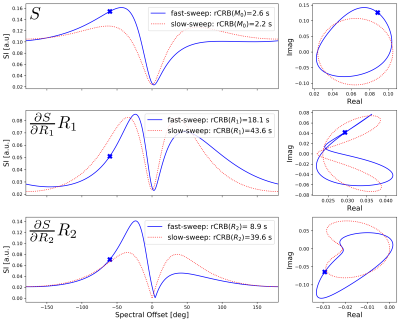
To investigate the effect of changing the modulation or sweeping speed in an fmSSFP sequence, we simulate a conventional bSSFP signal response using the Bloch equations where the transmitter phase of the nnn-th pulse is modulated according to$$\phi(n)= 180^\circ n + 360^\circ \frac{n^2}{2P}$$
where $$$P$$$ is the period of the generated signal and controls the sweeping speed. Two representative signal time courses are shown in Fig. 1 with periods $$$P$$$=50000 (slow sweep, left column) and $$$P$$$=1616 (fast sweep, right column). To assess the sensitivity of the respective Bloch responses, a relative Cramér-Rao-bound (rCRB) analysis was performed similar to [4]:
$$ \text{rCRB(}M_0\text{)} = \sigma^{-2} T_\text{exp} \left[I^{-1}(\theta)\right]_{11} $$
$$ \text{rCRB(}R_1\text{)} = \sigma^{-2} R^2_1 T_\text{exp} \left[I^{-1}(\theta)\right]_{22} $$
$$ \text{rCRB(}R_2\text{)} = \sigma^{-2} R^2_2 T_\text{exp} \left[I^{-1}(\theta)\right]_{33} $$
with noise variance $$$\sigma^2$$$, Fisher-Information matrix $$$I(\theta)=\sigma^{-2}(DS)^{H}(DS)$$$, total duration of the sweep $$$T_\text{exp}$$$, and Jacobi matrix of the signal $$$DS$$$.
By increasing the modulation speed of the fmSSFP signal, the sensitivities of both T1 and T2 can be increased as relaxation effects are introduced into the signal time course, resulting in asymmetries that decouple the partial derivatives of R1 and R2 (Fig. 1).
METHODS
A 3D stack-of-stars trajectory is combined with a frequency-modulated SSFP sequence. Partitions are sampled in the innermost loop and Tiny-Golden-Angle sampling [5] is performed within each partition. All partitions are aligned to allow simple decoupling by inverse FFT prior to reconstruction.Image reconstruction is performed in the low-frequency Fourier subspace as detailed in [6,7] using BART [8] utilizing coil estimation by ESPIRIT [9] and gradient delay correction with RING [10].
For fast-sweep fmSSFP, in contrast to phase-cycled bSSFP, no closed-form signal models are available so far. Therefore, we modeled the signal time course within the framework of Extended Phase Graphs (EPG, [11]) and projected to the low-frequency Fourier subspace subsequently.
The presented approach was validated in a phantom study (NIST system standard model 130, TR=5.0 ms, FA=15°, 1×1×3 mm3, 1616 spokes per partition, 32 partitions, $$$P$$$=1616, 1616 prep. pulses, $$$T_\text{ACQ}$$$=4m20s) and in a volunteer without known illness (same acquisition parameters).
RESULTS
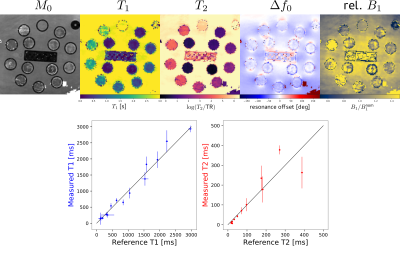
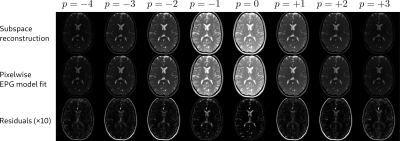
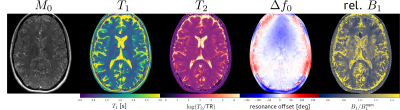
Figure 2 shows the parameter maps obtained after pixelwise fitting of the EPG signal model to the complex-valued subspace coefficients (exemplary slice). A ROI-based comparison with a gold standard T1 and T2 measurement (multiple inversion FLASH and single-echo spin echo) reveals good accuracy.Figure 3 shows reconstructed subspace coefficient maps, fitting results and fit residuals for the brain study. Fitting accuracy is excellent except for regions with subcutaneous fat or flowing CSF.
A synthesized time series can be computed from the reconstructed subspace coefficient maps and is shown in Figure 4.
Figure 5 shows parameter maps of the brain study similar to Fig 2. A ROI-based analysis for white and gray matter showed good agreement for both T1 and T2 with literature findings [12,13]. Similar to the phantom study, a coupling between M0 and relative B1 can be observed.
DISCUSSION & CONCLUSION
In this work, we demonstrated that fmSSFP can be sensitized to T1 and T2 by increasing the modulation speed. The reason for this effect might lie in the fact that for a slow or "quasistatic" modulation, the system stays in a memoryless steady state while a fast sweep introduces relaxation effects that depend on the state at previous time points. This signal behaviour enables decoupling of T1 and T2 dependencies without increasing the repetition time as suggested in [14].Several properties render this sequence very attractive for 3D multi-parametric mapping, which are a) continuous data acquisition without intermediate preparation phases, b) off-resonance-resolved reconstruction, and c) availability of a subspace model.
Initial results are promising and we believe fast-sweep fmSSFP to be an excellent candidate for fast and comprehensive multi-parametric mapping. As a next step, the observed coupling between $$$M_0$$$ and relative $$$B_1$$$ needs to be analyzed and eventually overcome.
A future integration of this signal model into a non-linear model-based reconstruction could help to better decouple individual parameter maps (e.g. $$$M_0$$$ from relative $$$B_1$$$) by incorporating prior knowledge and advanced regularization.
Acknowledgements
Supported by the DZHK (German Centre for Cardiovascular Research)References
[1] Nguyen et al., "MIRACLE: Motion-Insensitive RApid Configuration ReLaxomEtry", JMRI 36.4 (2012)
[2] Shcherbakova et al., "PLANET: an ellipse fitting approach for simultaneous T1 and T2 mapping using phase‐cycled balanced steady‐state free precession." MRM 79.2 (2018)
[3] Foxall et al., "Frequency‐modulated steady‐state free precession imaging", MRM 48.3 (2002)
[4] Assländer et al., "Optimized quantification of spin relaxation times in the hybrid state" MRM 82.4 (2019)
[5] Wundrak et al., "Golden ratio sparse MRI using tiny golden angles." MRM 75.6 (2016)
[6] Roeloffs et al., "Frequency‐modulated SSFP with radial sampling and subspace reconstruction: A time‐efficient alternative to phase‐cycled bSSFP." MRM 81.3 (2019)
[7] Roeloffs et al., "Joint T1/T2 mapping with frequency-modulated SSFP, radial sampling, and subspace reconstruction.", Proc. ISMRM 2018, 3702
[8] BART 0.6.00 Toolbox for Computational Magnetic Resonance Imaging, DOI: 10.5281/zenodo.3934312
[9] Uecker et al.. "ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA", MRM 71.3 (2014)
[10] Rosenzweig et al., "Simple auto‐calibrated gradient delay estimation from few spokes using Radial Intersections (RING).", MRM 81.3 (2019)
[11] Hennig et al., "Echoes—how to generate, recognize, use or avoid them in MR‐imaging sequences. Part I: Fundamental and not so fundamental properties of spin echoes" Concepts in Magnetic Resonance 3.3 (1991)
[12] Gelman et al., "MR imaging of human brain at 3.0 T: preliminary report on transverse relaxation rates and relation to estimated iron content.", Radiology 210.3 (1999)
[13] Ethofer, et al. "Comparison of longitudinal metabolite relaxation times in different regions of the human brain at 1.5 and 3 Tesla.", MRM 50.6 (2003)
[14] Shcherbakova et al., "On the accuracy and precision of PLANET for multiparametric MRI using phase‐cycled bSSFP imaging", MRM 81.3 (2019)
Figures