3045
Residual T2 dependent bias of T1 times estimated with the Variable Flip Angle approach at 7T: Evaluation and recommendations.1Wellcome Centre for Human Neuroimaging, UCL Queen Square Institute of Neurology, University College London, London, United Kingdom, 2Centre de Résonance Magnétique des Systèmes Biologiques, UMR 5536, CNRS/University Bordeaux, Bordeaux, France
Synopsis
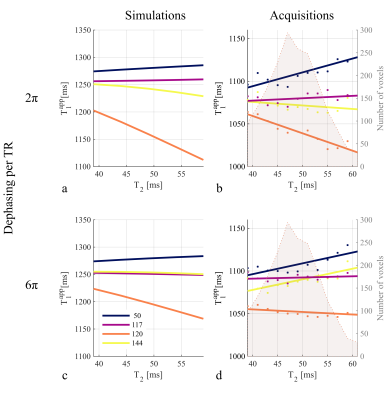
Imperfect spoiling introduces a bias in T1 times estimated with the Variable Flip Angle approach. Correction factors accounting for B1+ inhomogeneities have been proposed but a T2 dependent bias is expected to remain. Here we assess the amplitude of this effect at 7T with a commonly used multi-echo protocol and multiple radiofrequency spoiling increments and gradient spoiler moments. The T2 dependence is observed in-vivo and varies across spoiling conditions. Given that correction schemes don’t account for T2 variability, we recommend to use the least sensitive increment, such as 117° or 144°, in association with sufficient spoiling gradient (6π per TR).
Introduction
The Variable Flip Angle (VFA) approach estimating the longitudinal relaxation time (T1) assumes perfect spoiling of the transverse magnetization across TR. Despite gradient and radiofrequency (RF) spoiling, this condition is rarely met resulting in error in the estimated T1 times (T1app). Given that the error is dependent on B1+ efficiency, correction based on a transmit field map has been proposed1. Although comparatively small, T2 dependence is also expected in T1app. We investigate the amplitude of the T2 dependent bias observed in T1 times estimated with the VFA approach at 7T in different spoiling conditions. Unlike B1+ efficiency, a T2 map cannot be easily or rapidly acquired preventing a correction scheme from being used. An interesting alternative would consist of carefully choosing an RF spoiling increment that minimizes T2 dependence. We attempt in this work to provide guidelines regarding the choice of spoiling parameters in the Multi-parameter Mapping protocol2 to most accurately estimate T1 times at 7T.Methods
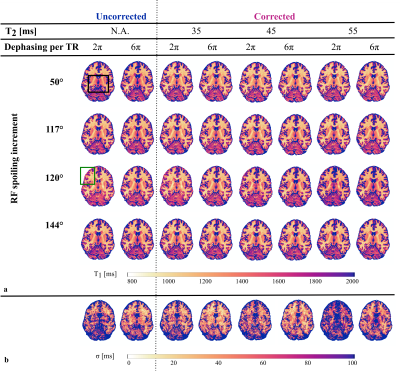
In-vivo acquisitionsEight T1app maps were acquired on one healthy volunteer on a 7T Terra Siemens scanner with the MPM protocol using 4 RF spoiling increments (φ0), carefully chosen for their distinct behaviour observed in simulations: 50°, 117°, 120° and 144°, and 2 spoiling gradient moments resulting in 2π and 6π dephasing per TR. Key parameters are: multi-echo spoiled gradient echo with TR=19.5ms, flip angles of α1=6° and α2=26°, 6 echoes with TE between 2.56 and 11.66ms, isotropic resolution of 1mm3. Additionally, transmit field maps (fB1+) were acquired with the Bloch-Siegert approach3 to compute T1app maps as follows4:
$$T_1^{app}=-\frac{TR}{ln(E_1)}\space with \space E_1=\frac{S_2-S_1.\frac{sin(α_2^c)}{sin(α_1^c)}}{S_2.cos(α_2^c)-S_1.cos(α_1^c)\frac{sin(α_2^c)}{sin(α_1^c)}}and\begin{cases}α_1^c=α_1.\frac{f_{B_1^+}}{100} \\ α_2^c=α_2.\frac{f_{B_1^+}}{100} \end{cases}\space(Eq.1)$$
Reference T1 and T2 maps were obtained from the mono-exponential fitting of 10 single-slice spin-echo acquisitions with and without pre-inversion pulse respectively and variable TIs or TEs respectively. Relevant parameters are: TR=10s, voxel size of 1.2×1.2×3.5mm3, TEs between 29 and 129ms for the T2 measurement, TE=29ms and TIs between 100 and 5000ms for the T1 measurement. An estimate of the apparent diffusion coefficient (ADC) was also obtained with diffusion-weighted spin-echo EPI acquisitions. T1app maps were co-registered to the reference T1 and T2 maps with SPM12.6 (https://www.fil.ion.ucl.ac.uk/spm/) to assess the T2 dependency of T1app in a region with comparatively homogeneous T1 (1100<T1<1350ms) as estimated in the reference T1 map, thereby minimizing the potential confounding factor of anatomical variability.
Numerical simulations
Numerical simulations of the MPM protocols were performed with the Extended Phase Graph (EPG) framework (https://sycomore.readthedocs.io/5), including diffusion effects6, for a range of expected T2 and T1 times and transmit field efficiency (fB1+). The diffusion coefficient D was fixed to 0.8µm²/ms. Correction factors for imperfect spoiling were computed from these simulations as described in1:
$$T_1=A(f_{B_1^+})+B(f_{B_1^+}).T_1^{app}\space with\begin{cases}A(f_{B_1^+})=a_2.f_{B_1^+ }^2+a_1.f_{B_1^+}+a_0\\B(f_{B_1^+})=b_2.f_{B_1^+}^2+b_1.f_{B_1^+}+b_0\end{cases}\space (Eq.2)$$
Three sets of correction factors for each spoiling condition were computed with T2 fixed to 35, 45 and 55ms and applied to T1app maps to correct for imperfect spoiling.
Results
Reference T2, T1 and ADC values in the region of interest were estimated to be 47±6ms, 1260±50ms and 0.7±0.1mm2/ms respectively. The T2 dependence of T1app obtained from the MPM protocols was observed in-vivo at 7T as was the impact of the spoiling conditions (Fig.1b,d). The T2 dependence generally followed the predictions of numerical simulations (Fig.1a,c)).φ0 of 50° and 120° were the most sensitive to T2 as predicted by numerical simulations (+30ms and -51ms respectively). 117° and 144° showed the smallest T2 dependence (variation smaller than 10ms). In line with simulations, the in-vivo T2 dependence decreased for 120° and was negligibly impacted for 117° and 50° when increasing gradient spoiling. As predicted, the T2 dependence of 144° was also impacted but the measured dependence was not as low as predicted. Difference across T1app maps (Fig.2a) were visible and highlighted by the map of the standard deviation (σ) across φ0 (Fig.2b). The variability across φ0 generally decreased with higher spoiling gradient. After correction for imperfect spoiling, the variability decreased when assuming a global T2 of 45ms in the correction factors, and decreased even further with a T2 of 35ms. However, it increased with correction factors assuming a T2 of 55ms.
Discussion
Although T2 shortens at 7T, and the diffusion spoiling is increased with a multi-echo protocol, a remaining T2 dependence of the estimated T1 times due to imperfect spoiling was observed. Ultimately, this resulted in a dependence of the corrected T1 maps on the choice of T2 used to compute the correction factors. A T2 of 35ms reduced the variability across φ0 although the estimated T2 with a spin-echo sequence was slightly longer. Given that only a global T2 is used, the residual spatial T2 dependency will remain after correction. A careful choice of the RF spoiling increment and the spoiling gradient moment is therefore recommended to minimize the T2 dependency. Although 50° is commonly used, 117° or 144° with relatively high spoiling gradient. would be preferable.Conclusion
We demonstrated the T2 dependent bias of T1 estimated with VFA at 7T resulting from imperfect spoiling. We observed a manifestation of the diffusion effect at 7T in-vivo with reasonable gradient amplitude and commonly used protocols. We recommend the use of an RF spoiling increment that minimizes T2 dependency in combination with a relatively high spoiling gradient moment.Acknowledgements
The Wellcome Centre for Human Neuroimaging is supported by core funding from the Wellcome [203147/Z/16/Z].References
1. Preibisch C, Deichmann R. Influence of RF spoiling on the stability and accuracy of T1 mapping based on spoiled FLASH with varying flip angles. Magnetic Resonance in Medicine 2009;61:125–135 doi: 10.1002/mrm.21776.
2. Weiskopf N, Suckling J, Williams G, et al. Quantitative multi-parameter mapping of R1, PD*, MT, and R2* at 3T: a multi-center validation. Front Neurosci 2013;7 doi: 10.3389/fnins.2013.00095.
3. Corbin N, Acosta‐Cabronero J, Malik SJ, Callaghan MF. Robust 3D Bloch-Siegert based mapping using multi-echo general linear modeling. Magnetic Resonance in Medicine 2019;82:2003–2015 doi: 10.1002/mrm.27851.
4. Mohammadi S, D’Alonzo C, Ruthotto L, et al. Simultaneous adaptive smoothing of relaxometry and quantitative magnetization transfer mapping. 2017 doi: 10.20347/WIAS.PREPRINT.2432.
5. Lamy J, Loureiro de Sousa P. Sycomore: an MRI simulation toolkit. In: ISMRM. Virtual; 2020. p. 2072.
6. Weigel M, Schwenk S, Kiselev VG, Scheffler K, Hennig J. Extended phase graphs with anisotropic diffusion. Journal of Magnetic Resonance 2010;205:276–285 doi: 10.1016/j.jmr.2010.05.011.
Figures