3007

Cerebro-cerebellar impact on brain dynamics in a single-subject with cerebellar ataxia
Silvia Maria Marchese1, Fulvia Palesi2,3, Mariagrazia Bruzzone4, Anna Nigri4, Stefano D'Arrigo5, Chiara Pantaleoni5, Claudia AM Gandini Wheeler-Kingshott2,3,6, Egidio D'Angelo2,3, and Paolo Cavallari1
1Human Physiology Section of the DePT, Università degli Studi di Milano, Milano, Italy, 2Department of Brain and Behavioral Science, Università degli Studi di Pavia, Pavia, Italy, 3Brain Connectivity Center Research Department, IRCCS Mondino Foundation, Pavia, Italy, 4Neuroradiology Department, Fondazione IRCCS Istituto Neurologico "C. Besta", Milano, Italy, 5Developmental Neurology Department, Fondazione IRCCS Istituto Neurologico "C. Besta", Milano, Italy, 6Department of Neuroinflammation, UCL Queen Square Institute of Neurology, Faculty of Brain Sciences, University College London, NMR Research Unit, Queen Square MS Centre, London, United Kingdom

Synopsis

The simulation of whole-brain dynamics in a single-subject affected by Joubert syndrome (non-progressive pediatric cerebellar ataxia), allowed us to investigate the impact of cerebro-cerebellar connectivity in a brain network with cerebellar dysfunction. The prediction power resulted strongly disturbed with the exclusion of the cerebro-cerebellar network from the generation of cerebral activity. These preliminary results suggest that compensatory mechanisms and plasticity must have taken place in the damaged cerebellum itself to support whole brain functional dynamics.

Introduction

Pediatric cerebellar ataxias (PCAs) are a clinically heterogeneous group of neurological disorders characterized by impairment in motor coordination and balance. Within PCA, patients with Joubert syndrome can often surprisingly show postural motor behaviour comparable to that of healthy subjects1, which may depend on the non-progressive nature of the pathological form. Indeed, it has been demonstrated that children with congenital neuronal dysfunctions and even complete cerebellar agenesis2 are able to recover limb functionality, so as to perform even complex motor tasks3. Such a compensation could be justified by an hyper-function of the remaining brain areas which have to cope with a stable lesion creating new neural pathways. Since it is interesting to figure out which and how different neural substrates play a role in the functional compensation, we simulated whole-brain dynamics starting from a multimodal dataset within “The Virtual Brain (TVB)” modeling framework4,5. TVB has recently been developed to integrate structural and functional connectomes with computational models that simulate global brain dynamics at single-subject level and has been used to investigate the impact of cerebro-cerebellar connectivity to generate whole-brain dynamics6. Here, cerebralspatio-temporal dynamics including or excluding the cerebro-cerebellarconnections were calculated to investigate the putative compensatory role played by neural structures in cerebellar ataxia.

Methods

Subject
Data were obtained in one single patient with Joubert syndrome (male; 21 years; hospitalized at the Istituto Neurologico "C. Besta", Milano) by using a Philips 3T Achieva scanner. A 3DT1-weighted volume (MPRAGE sequence, TR/TE= 8.28/3.83ms, 1mm isotropic resolution), diffusion-weighted images (SE-EPI sequence, TR/TE=8400/85ms, 2.5 mm isotropic resolution, b=1000,2000 s/mm2, 32 isotropically distributed directions/shell and 7 b0 images), and resting state fMRI (rs-fMRI) series (GE-EPI sequence, TR/TE= 2400/30ms, 3mm isotropic resolution, 200 volumes) were acquired.
Multimodal dataset
3DT1-weighted images were segmented (FSL7) as white matter, gray matter (GM), subcortical GM, and cerebrospinal fluid. From diffusion-weighted data, 30 million streamlines whole-brain Anatomically-Constrained Tractography8,9,10 was performed (MRtrix311). An ad-hoc atlas comprising 126 regions was created combining 93 cerebral, including cortical and subcortical structures (Automated Anatomical Labeling12), and 33 cerebellar (SUIT13) labels. The structural connectivity (SC) matrix was obtained combining the atlas with the whole-brain tractography and using the normalized number of streamlines as edges and cortical/subcortical labels as nodes. rs-fMRI data were processed using the Data Processing and Analysis of Brain Imaging (DPABI,)14,15 and Statistical Parametric Mapping (SPM16) within MATLAB17. Slice timing, brain extraction, and head motion correction (Friston 24 method) were performed. ROI time-courses were extracted for each node and a functional connectivity (FC) matrix was evaluated correlating time-courses between pair of nodes with Fisher z-transformed coefficient. This FC matrix was thresholded at 0.12066 to obtain the final experimental FC (expFC) matrix.
TVB simulation
The SC matrix defined the long-range connectivity of the brain. A reduced Wong-Wang model18 was chosen to generate the mean activity of each node (simulated FC, simFC). A model inversion approach was used to tune the global coupling parameter within the whole-brain network, including cerebro-cerebellar connectivity. The value for which the correlation between expFC and simFC presented its maximum was assumed as the optimal global coupling (Gcoupl). Brain dynamics were simulated for 6 minutes and a specific time-series for each node was provided. Pearson correlation coefficient (PCC) between temporal signals was estimated to calculate the final simFC matrix. The simulation was repeated for three conditions: 1) whole-brain network, 2) cerebral subnetwork, 3) embedded cerebro-cerebellar subnetwork.
Statistics
PCC was used to assess the coherence between expFC and simFC in the three previous conditions, hence either including or excluding the cerebro-cerebellar connectivity. The correlation coefficient between SC and simFC was also calculated.

Results

Gcoupl value and PCC between SC-simFC, expFC-simFC are reported for the three conditions (Table 1). SC, expFC, whole-brain simFC, cerebral simFC and embedded cerebro-cerebellar simFC matrices are presented (Figure 1). PCC between expFC and simFC results strongly decrease (0.162) when cerebro-cerebellar connectivity is excluded from simulation (see Table 1).

Discussion

This work aimed to investigate brain functional connectivity in a subject with a non-progressive cerebellar dysfunction using TVB, which was developed for patient-specific analysis. Despite the brain dynamics analysis was performed on a single-subject, our preliminary data highlighted that PCC, i.e. prediction power, strongly decreases when we exclude cerebro-cerebellar connectivity from the generation of cerebral activity. This result seems to be in agreement with the hypothesis that patients with this non-progressive disorder are able to recover motor functionality thanks to compensatory strategies implemented by cerebellar plasticity, itself. The cerebellum could create new neural pathways with other neural substrates, becoming essential in brain networks despite it is itself damaged. Future studies are warranted to verify that this is the case in more subjects and to focus on specific neural candidates that could be involved. A possible candidate may be the subtalmic nucleus, which has been shown to reciprocally connect striatum and cerebellum19–21. A functional compensatory action of the cerebellum during basal ganglia pathology22,23 has been recently described, while a putative compensatory role of the basal ganglia on cerebellar diseases is still to be demonstrated.

Acknowledgements

This research received funding by H2020 Research and Innovation Action Grants Human Brain Project 785907 and 945539 (SGA2 and SGA3) and by the MNL Project “Local Neuronal Microcircuits” of the Centro Fermi (Rome, Italy) to ED and FP. CGWK receives funding from the UK MS Society (#77), Wings for Life (#169111), Horizon2020 (CDS-QUAMRI, #634541), BRC (#BRC704/CAP/CGW)

References

  1. Farinelli V, Palmisano C, Marchese SM, et al. Postural Control in Children with Cerebellar Ataxia. Appl Sci. 2020;10:1–13.
  2. Titomanlio L, Romaniello R, Borgatti R. Cerebellar agenesis. Handb Cerebellum Cerebellar Disord. Epub 2005.:1855–1872.
  3. Vining EPG, Freeman JM, Pillas DJ, et al. Why would you remove half a brain? The outcome of 58 children after hemispherectomy - The Johns Hopkins Experience 1968 to 1996. Pediatrics. 1997;100:163–171.
  4. Sanz Leon P, Knock SA, Woodman MM, et al. The Virtual Brain: a simulator of primate brain network dynamics. Front Neuroinform. 2013;7:1–23.
  5. Ritter P, Schirner M, Mcintosh AR, Jirsa VK. The Virtual Brain Integrates Computational Modeling. Brain Connect. 2013;3:121–145. 6.
  6. Palesi F, Lorenzi RM, Casellato C, et al. The Importance of Cerebellar Connectivity on Simulated Brain Dynamics. 2020;14:1–11.
  7. https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/.
  8. Smith RE, Tournier JD, Calamante F, Connelly A. Anatomically-constrained tractography: Improved diffusion MRI streamlines tractography through effective use of anatomical information. Neuroimage. 2012;62:1924–1938.
  9. Jeurissen B, Tournier JD, Dhollander T, Connelly A, Sijbers J. Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. Neuroimage. Elsevier Inc.; 2014;103:411–426.
  10. Tournier J-D, Calamante F, Connelly A. Improved probabilistic streamlines tractography by 2 nd order integration over fibre orientation distributions. Proc Int Soc Magn Reson Med. 2010. p. 1670.
  11. https://www.mrtrix.org.
  12. Tzourio-Mazoyer N, Landeau B, Papathanassiou D, et al. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage. 2002;15:273–289.
  13. Diedrichsen J, Balsters JH, Flavell J, Cussans E, Ramnani N. A probabilistic MR atlas of the human cerebellum. Neuroimage. 2009;46:39–46.
  14. Yan C, Wang X, Zuo X, Zang Y. DPABI : Data Processing & Analysis for ( Resting-State ) Brain Imaging. Neuroinformatics [online serial]. Neuroinformatics; Epub 2016.:339–351. Accessed at: http://dx.doi.org/10.1007/s12021-016-9299-4.
  15. http://rfmri.org/dpabi.
  16. https://www.fil.ion.ucl.ac.uk/spm/.
  17. https://it.mathworks.com/products/matlab.html.
  18. Wong KF, Wang XJ. A recurrent network mechanism of time integration in perceptual decisions. J Neurosci. 2006;26:1314–1328.
  19. Bostan AC, Dum RP, Strick PL. Cerebellar networks with the cerebral cortex and basal ganglia. Trends Cogn. Sci. 2013. p. 241–254
  20. Bostan AC, Dum RP, Strick PL. The basal ganglia communicate with the cerebellum. Proc Natl Acad Sci U S A. 2010;107:8452–8456.
  21. Hoshi E, Tremblay L, Féger J, Carras PL, Strick PL. The cerebellum communicates with the basal ganglia. Nat Neurosci. 2005;8:1491–1493.
  22. Heman P, Barcia C, Gómez A, et al. Nigral degeneration correlates with persistent activation of cerebellar Purkinje cells in MPTP-treated monkeys. Histol Histopathol. 2012;27:89–94.
  23. Rolland AS, Herrero MT, Garcia-Martinez V, Ruberg M, Hirsch EC, François C. Metabolic activity of cerebellar and basal ganglia-thalamic neurons is reduced in parkinsonism. Brain. 2007;130:265–275.

Figures

Table 1: Parameters forwhole-brain network, cerebral subnetwork and embedded cerebro-cerebellar subnetwork.Optimal value for global coupling (Gcoupl) and Pearson correlation coefficients (PCC) between structural connectivity (SC), experimental (expFC) and simulated functional connectivity (simFC) are reported.

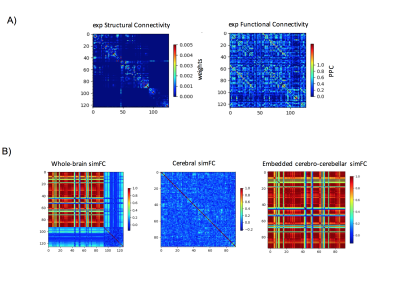
Figure 1: A) Experimental matrices of structural connectivity (expSC) and functional connectivity (expFC) in the patient with Joubert syndrome. B) Simulated functional connectivity (simFC) matrices for whole-brain network (left), cerebral subnetwork (center) and embedded cerebro-cerebellar subnetwork (right). In each matrix, rows and columns represent a specific brain region (node), while each intersection point represents a connection, weighted by the number of streamlines, between two nodes (edge).

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)
3007