Introduction:

In previous works [1], [2] accelerated 3D-T1rho mapping using parallel MRI (pMRI) and compressed sensing (CS) have been successfully demonstrated. However, most of the proposed changes were related to reconstructions. In [3], it was first demonstrated improvements when a different acquisition is used. Here, we study the use of machine learning (ML) approaches dedicated to learning the optimal sampling pattern (SP). One recently-developed ML algorithm for fast learning an effective accelerated SP is the bias-accelerated subset selection (BASS) [4]. BASS can learn an efficient SP for a given data and reconstruction method, improving reconstruction quality. However, it is still unknown how much improvement is obtained for quantitative mapping, in particular T1rho mapping of knee cartilage.
Here, we investigate the use of BASS to learn optimized SPs for the T1rho mapping of the knee cartilage, considering different kinds of accelerated image reconstructions that exploit sparsity and low-rankness. We also extended the method to perform jointly optimization of the SP and the regularization parameters.

Methods:

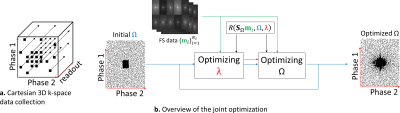
First, Cartesian 3D+time k-t-space data is separated into multiple 2D+time slices by using FFT in the frequency-encoding (readout) direction (see Figure 1a). The CS and low rank (LR) reconstructions [1,5] are obtained by solving:
$$\hat{\mathbf{x}}=\arg\min_\mathbf{x} \left( ||\bar{\mathbf{m}}-S_ΩFC\mathbf{x}||_2^2+λP(\mathbf{x}) \right)\approx R(\bar{\mathbf{m}},Ω, λ),$$
for each slice, where $$$\mathbf{x}$$$ represents the 2D+time image slices of size $$$N_x\times N_y\times N_t$$$ (in our experiments this is $$$128 \times 64 \times 10$$$) which denotes vertical $$$N_x$$$ and horizontal $$$N_y$$$ sizes and time $$$N_t$$$. $$$\bar{\mathbf{m}}= S_Ω\mathbf{m}$$$ is the undersampled multicoil k-t-space data. $$$C$$$ denotes the coil sensitivities transform and low-order phase correction, compensating image phase and mapping $$$\mathbf{x}$$$ into multicoil-weighted images of size $$$N_x \times N_y \times N_t \times N_c$$$, with number of coils $$$N_c$$$. $$$F$$$ represents the spatial FFTs, which are $$$N_t \times N_c$$$ repetitions of the 2D-FFT, $$$S_Ω$$$ is the sampling function using SP $$$Ω$$$ (same for all coils) and $$$λ$$$ is the regularization parameter, see details in [1]. The SP contains the k-t-space points to be sampled in the phase-encoding positions of the Cartesian 3D+time acquisition. The regularization functions considered are: $$$l_1$$$-norm, as $$$P(x)=||Tx||_1$$$, where $$$T$$$ is the spatiotemporal finite differences (STFD); and low rank (LR), using nuclear-norm of $$$\mathbf{x}$$$ (reshaped as a matrix [6]), given by $$$||\mathbf{x}||_*$$$, and low-rank plus sparse where $$$x=l+s$$$ is a decomposition of $$$x$$$ on a sparse part $$$s$$$ and a low rank $$$l$$$ part and $$$ λP = λ_l ||l||_*+λ_s ||Ts||_1$$$ [7], where $$$T$$$ is spatial finite difference (L+S SFD). We use the iterative algorithm MFISTA-VA [8], to obtain $$$R(\bar{\mathbf{m}},Ω,λ)$$$, that approximates the minimizing $$$\mathbf{x}$$$.
The learning process of the SP follows [4], extended to also find the optimal $$$λ$$$:
$$\hat{Ω},\hat{λ} = \arg\min_{Ω, λ} \sum_{i=1}^{N_i} f( \mathbf{m}_{i} , FC R(S_Ω \mathbf{m}_{i}, Ω, λ)) $$
$$$N_i$$$ is the number of data items used for learning. We use fully-sampled pMRI data $$$\mathbf{m}_{i}$$$, of size $$$N_x \times N_y \times N_t \times N_c$$$ (size $$$128 \times 64 \times 10 \times 15$$$ in the experiments) obtained from 3D+time data after separating into multiple slices, and:
$$f(\mathbf{m}_{i},\hat{\mathbf{m}}_{i})= \frac{|| \mathbf{m}_{i}- \hat{\mathbf{m}}_{i} ||_2^2}{|| \mathbf{m}_{i}||_2^2 }$$
is the normalized squared error (NSE). This joint optimization procedure is separated into two alternated procedures: the optimal regularization parameter, $$$\hat{λ}$$$, is obtained using bisection line search method [9], and the optimal SP, $$$\hat{Ω}$$$, is obtained with BASS [4] (see Figure 1b).
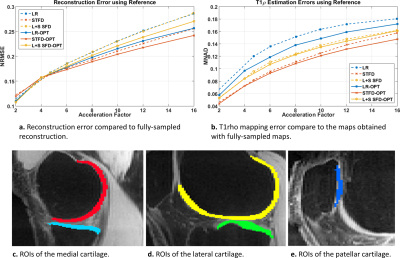
After the reconstruction of all slices, T1rho mapping of cartilage was obtained using a complex-valued fitting with mono-exponential models using non-linear least squares, following [3]. The reconstruction error was evaluated with normalized root mean squared error (NRMSE) using the entire 3D volume, the T1rho mapping error was evaluated using the median of normalized absolute deviation (MNAD) on specific slices of the medial, lateral, and patellar cartilage (see Fig. 3c-e).

Experiments:

We used normalized fully-sampled 3D-T1rho data of healthy volunteers (n=8, mean age=26.6±1.5) with 10 spin-lock times (TSLs of 2/4/6/8/10/15/25/35/45/55ms). Half of the data was used for training (n=4). Poisson disk [1] was used as a reference and initial SP. A central k-space of 39x19 (for all AF) of the first TSL is used for coil sensitivity-map estimation [10] low-order phase estimation [11].

Results and Discussion:

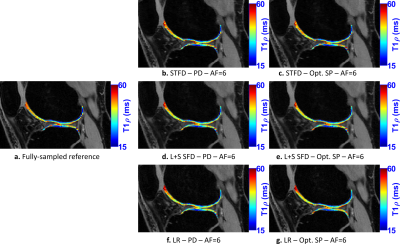
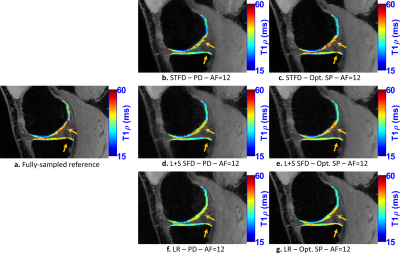
In Fig. 2, we evaluate the performance of optimized SPs for the three CS methods tested: LR, STFD, and L+S SFD, compared to the Poisson disk SP (which was also used as initial SP in BASS). In Figure 3a the improvement in reconstruction is shown, with NRMSE, in which, on average, LR improved by 6.5%, L+R SFD improved by 4.4%, and STFD improved by 3.3%. In Figure 3b the improvement in T1rho values of cartilage is shown, in MNAD, in which, on average, LR improved by 11.5%, L+R SFD improved by 3.2%, and STFD improved by 5.4%. The optimization of the SP has more impact at higher AFs.
Figures 4 and 5 show some representative examples of T1rho maps of lateral knee cartilage, for AF=6 and medial knee cartilage, for AF=12 respectively.

Conclusion:

The learned sampling pattern (SP) improved the quality of image reconstruction and T1rho mapping of knee cartilage. The improvements are more significant at high acceleration factors, which is important since it adds to the efforts of making MRI scans even faster.

Acknowledgements

This work was supported in part by NIH grants R21 AR075259, R01 AR076328, R01 AR067156, R01 AR070297, and R01 AR068966, and was performed under the rubric of the Center for Advanced Imaging Innovation and Research (CAI2R, www.cai2r.net) an NIBIB Biomedical Technology Resource Center (NIH P41 EB017183).