Introduction

Real-time phase-contrast (rt-PC) MRI has several advantages (faster, free-breathing scan, insensitivity to arrhythmia) over clinical standard ECG-gated breath-hold PC MRI. Several studies have applied compressed sensing (CS) to highly accelerate rt-PC to achieve clinically acceptable spatio-temporal resolution. However, their lengthy image reconstruction hinders clinical translation. Deep learning (DL) is showing great potential for rapid reconstruction of accelerated MRI images^1-3. In this study, we sought to implement a rapid image reconstruction pipeline for rt-PC MRI using a generative adversarial network (GAN) with optimal loss terms and test its accuracy for quantification of blood flow velocities in the left atrium (LA) and mitral valve (MV).

Methods

Data acquisition: We used existing 28.8-fold accelerated rt-PC raw k-space datasets (230 2D+time datasets; 60 frames per set) collected from 51 patients (33 males and 18 females, mean age = 68 ± 13 years) at up to three locations (mitral valve, left atrium). The training set for neural networks comprised of 210 2D+time datasets from 41 randomly selected patients. The remaining 20 2D+time datasets from 10 patients were used for testing. Relevant image parameters are FOV=300x300mm², matrix size=144x144, spatial resolution=2.1x2.1mm², slice thickness=8mm, TE/TR=3.78/8.5 ms, 5 radial spokes per frame, acceleration factor=28.8, flip angle=15°, receiver bandwidth=793Hz/pixel, temporal resolution=42.5ms, and scan time=10s.
Image reconstruction: The image reconstruction pipeline was divided into two steps: pre-processing (i.e. coil-combined, zero-filled NUFFT) and de-aliasing. During pre-processing, GPU-accelerated NUFFT was used to grid the radial k-space data onto the Cartesian space, and multi-coil, zero-filled images were combined as the weighted sum using self-calibrated coil sensitivities. For de-aliasing, we implemented and compared two GANs with respect to GPU-accelerated GROG-GRASP^4,5 (i.e. compressed sensing) as reference: (1) GAN with MSE loss and perceptual loss, and (2) GAN with weighted-MSE loss and perceptual loss. All image reconstruction methods were implemented on a GPU workstation (Tesla V100 32 GB memory, NVIDIA): Matlab for GROG-GRASP; Pytorch for GAN.
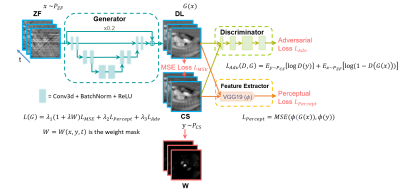
Neural networks: Figure 1 shows the network structure and loss functions for the proposed GAN with different loss options. The network had 3 layers with 32 features in the first layer, 3x3x3 (x-y-time) convolutional kernel size, no max-pooling to reduce temporal blurring, a residual connection with a weight of 0.2 to balance the sharpness of the output images and the amount of remaining streaking artifact. All frames were cropped to 104x104 in-plane matrix size for more efficient training. Training for 75 epochs took 25-36 hours depending on the network architecture. Perceptual loss was computed from the output of a pre-trained VGG-19 to extract high-frequency information. The coefficients of MSE loss, perceptual loss, and adversarial loss were determined empirically. Our rationale for weighted-MSE loss is to emphasize brighter signals in velocity-encoded image associated with flowing blood over static tissues during training. For details on how weighted MSE loss is determined, see Figure 2. All neural networks were implemented with complex convolutions for analytical correctness⁶. Reference data and velocity-encoded data were separated into two channels.
Data analysis: We performed background phase correction using the previously described method⁷. Regions of interest corresponding to mid LA and MV were manually drawn, and the same contours were used across GROG-GRASP and GAN images; we quantified the peak velocity and mean velocity. The blur metric⁸ was quantified on a 0 to 1 continuous scale, where 0 is defined as sharpest and 1 is defined as blurriest. Appropriate statistical analyses (ANOVA for three groups, paired t-test for two groups) were conducted, where p < 0.001 was considered statistically significant.

Results

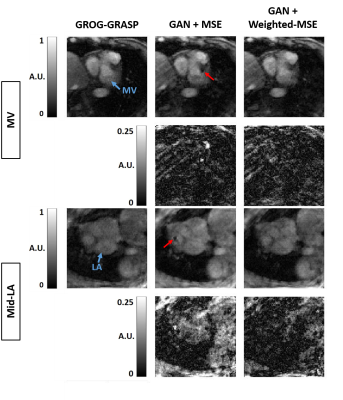
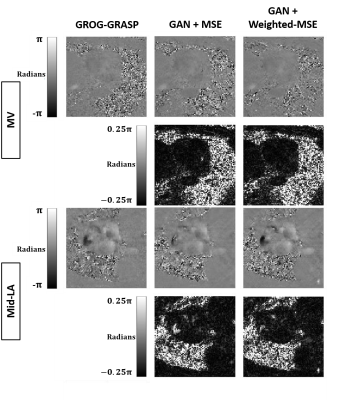
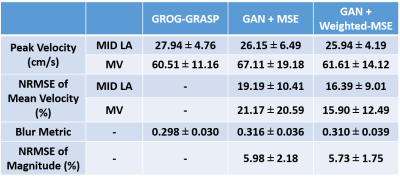
Compared with GROG-GRASP (51.5 ± 19.3 s), de-aliasing time for GAN (0.084 ± 0.008 s) was 613 times faster (p < 0.001). Figure 3 compares the magnitude images reconstructed using GROG-GRASP, GAN with MSE loss, and GAN with weighted MSE loss, as well as their difference images with respect to GROG-GRASP. Compared with MSE loss, weighted MSE loss reduced signal difference compared with GROG-GRASP. Similarly, the same trends are shown for phase-contrast images in Figure 4. Summarizing the results over ten patients, neither the blur metric nor peak velocity (mid LA or MV) was significantly (p > 0.99) different between GROG-GRASP, GAN with MSE loss, and GAN with weighted-MSE loss (see Table 1). Compared with GROG-GRASP, normalized root-mean-square-error (NRMSE) of mean velocity was significantly (p < 0.04) lower for GAN with weighted-MSE loss than GAN with MSE loss for both mid LA and MV planes, whereas the NRMSE of magnitude image was not significantly (p = 0.46) different between GAN with MSE loss (5.98 ± 2.18%) and GAN with weighted MSE loss (5.73 ± 1.75%).

Conclusion

In this study, we implemented a rapid image reconstruction pipeline for rt-PC MRI using GAN, which was 613-times faster than compressed sensing. Compared with MSE loss, weighted MSE loss reduced signal error, which resulted in improved accuracy in velocity measurements. Future work includes comparison of this GAN approach to variational² and unrolled¹ networks incorporating a data fidelity term while accounting for GPU memory efficiency and reconstruction accuracy.

Acknowledgements

This work was supported in part by the following grants: National Institutes of Health (R01HL116895, R01HL138578, R21EB024315, R21AG055954, R01HL151079) and American Heart Association (19IPLOI34760317).