2872

Deep generative manifold model: a novel approach for free breathing dynamic MRI

Qing Zou¹, Abdul Haseeb Ahmed¹, Prashant Nagpal¹, Rolf Schulte², and Mathews Jacob¹
¹University of Iowa, Iowa City, IA, United States, ²GE Global Research, Munich, Germany

Synopsis

Cardiac disease is a frequent comorbidity and cause of death in subjects with compromised pulmonary function (e.g. COPD). High-resolution and free breathing cine imaging sequences are necessary for the evaluation of cardiac function in such subjects. Several self-gated and manifold algorithms were introduced for free-breathing MRI with good success. The main focus of this work is to further reduce the scan time of current manifold methods. We introduce a novel unsupervised deep generative manifold framework to recover free-breathing cine data from around 7seconds/slice, which will facilitate the acquisition of the whole volume in under two minutes.

Purpose/Introduction

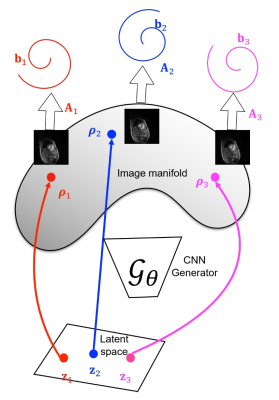
Self-gating methods are being widely used for free-breathing cine MRI [1]; these methods use k-space navigators to estimate the cardiac/respiratory phase, followed by the binning and recovery of measured data. Recently, manifold approaches including SToRM [2], which perform soft-gating based on k-space navigators are emerging as powerful alternatives. However, manifold methods that recover the entire image time-series rather than the binned images suffer from high memory demand and difficulty in using additional spatial regularization.
In this work, we introduce an unsupervised deep generative manifold (Gen-SToRM) model to overcome the challenges with traditional manifold models. Unlike supervised deep learning schemes that requires extensive training data, this approach learns the network from the k-t space data of the specific patient. We represent the images in the time series as compact nonlinear mappings of low-dimensional latent vectors, which capture the cardiac/respiratory phases. The nonlinear function is compactly represented using a deep CNN. The model is illustrated in Fig.1 and Fig. 2. Inspired by the deep image prior framework introduced for static imaging [3], we learn the CNN parameters and the latent vectors directly from the measured k-space data. The main benefit of this scheme is that the latent vectors that capture the cardiac/respiratory phase need not be estimated a-priori, which is often the most challenging and important aspect of self-gating and manifold methods. In addition, the proposed framework naturally brings in spatial and temporal regularization, facilitating the recovery of the images from short acquisitions.

Methods

We model the images in the time series as non-linear mappings $$$\rho_t = G_{\theta}(\mathbf{z}_t)$$$, where $$$\mathbf{z}_t$$$ are vectors that live in a low dimensional subspace. The non-linear mapping $$$G_{\theta}$$$ is represented by a deep CNN. The memory footprint of the scheme depends on the number of parameters $$$\theta$$$ and $$$\mathbf{z}$$$, which is orders of magnitude smaller than that of traditional manifold methods.
We propose to jointly optimize the network parameters $$$\theta$$$ and the latent variables $$$\mathbf{z}$$$ based on the given k-space data. We try to minimize the following cost function $$\mathcal C(\mathbf z,\theta)= \sum_{i=1}^N\|\mathcal A_i\left(\mathcal G_{\theta}[\mathbf z_i]\right) - \mathbf{b}_i\|^2 + \lambda_1 \underbrace{\|\nabla_{\mathbf z} \mathcal G_{\theta}\|^2}_{\scriptsize \mbox{network regularization}} + \lambda_2 \underbrace{\|\nabla_{t} \mathbf z_t\|^2 }_{\scriptsize\mbox{temporal regularization}}$$ to obtain the network parameters and the latent variables. This minimization problem is solved using stochastic gradient descent.

Results

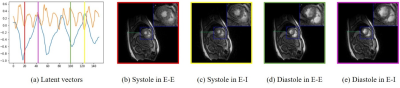
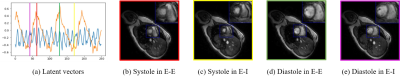
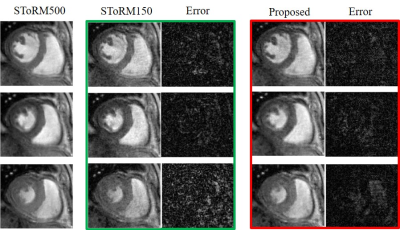
We demonstrate the results on two datasets, acquired on a GE 3T scanner acquired using a golden angle spiral GRE sequence. The sequence parameters are: TR = 8.4 ms, FOV = 320 mm x 320 mm, flip angle = 18, slice thickness = 8 mm. We consider the recovery from around 8 seconds of data/slice, which translates to 2.2 minutes of acquisition for the heart with 16 slices. Fig. 3 shows the reconstruction of one slice from the first dataset. Four different phases are shown in the figure and the corresponding latent vectors are given highlighted in the plot of the latent vectors. Fig. 4 shows the reconstruction of one slice from the second dataset and we also showed four different phases. This dataset is challenging and hence we use latent variable of size 4 x 1 for the reconstruction, which is different from the scenario for the first dataset, where we use latent vector of size 2x1. We also show the reconstruction comparison with SToRM, which is given in Fig. 5.

Conclusion

The experiments show the ability of the proposed scheme to reliably recover free breathing and ungated cardiac MRI from around 8 seconds/slice. This scheme does not require navigators for acquiring the data, which makes it directly applicable to golden angle radial/spiral acquistions.

Acknowledgements

This work is supported by by grants NIH 1R01EB019961-01A1and R01EB019961-02S. This work was conducted on an MRI instrument funded by 1S10OD025025-01

References

[1] Feng et al, MRM 2014.

[2] Poddar et al., IEEE TMI 2016.

[3] Ulyanov et al., IEEE CVPR 2018.

Figures

Fig. 1. Illustration of the proposed deep generative SToRM model. The proposed method models the images as the non-linear mapping $$$\mathcal{G}_{\theta}$$$ of some latent vectors $$$\mathbf{z}_i$$$ which lie in a very low dimensional space. Note that the same generator is used to model all the images in the dataset. The number of parameters of the generator and the latent variables is around the size of a single image, which implies a highly compressed representation. In addition, the structure of the CNN offers spatial regularization as shown in deep image prior.

Fig. 2. Illustration of the scheme. The latent vectors, which can be viewed as virtual gating signals, are fed into the deep generative model $$$\mathcal{G}_{\theta}$$$, which then generates the images in the time series. The optimization scheme facilitates the learning of the latent vectors and the parameters $$$\theta$$$ of the generative model from the measured k-t space data.

Fig. 3. Illustration of the framework of the proposed scheme on the first dataset. We plot the latent variables of 150 frames (~50 ms duration), which are learned from the k-t space data in (a). We show four different phases in the time series: systole in End-Expiration (E-E), systole in End-Inspiration (E-I), diastole in End-Expiration (E-E) and diastole in End-Inspiration (E-I). A thin green line is put around the liver in the image frame to indicate the respiratory phase. The latent vectors corresponding to the four different phases are indicated in the plot of the latent vectors.

Fig. 4. Illustration of the framework of the proposed scheme on the second dataset. Since this dataset has extensive respiratory motion , we use three latent variables. We plot the latent variables of 250 frames in time series. We showed four different phases in the time series: systole in End-Expiration (E-E), systole in End-Inspiration (E-I), diastole in End-Expiration (E-E) and diastole in End-Inspiration (E-I). The latent vectors corresponding to the four different phases are indicated in the plots of the latent vectors.

Fig. 5. Comparison with SToRM with longer acquisition time. The first column corresponds to the reconstructions from 500 frames (~ 25s of acquisition time), while the rest of the columns are recovered from 150 frames (~ 7.5s of acquisition time). The top row corresponds to the diastole phase, while the third row is the diastole phase. The second row is an intermediate one. We observe that the proposed reconstructions exhibit less blurring and artifacts, compared to SToRM150, which also uses the 7.5 s acquisition.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

2872