2869
Comparison of Region-Wise and Voxel-Wise Diffusion Signal Harmonisation via Z-scoring and ComBat1BioMedIA, Department of Computing, Imperial College London, London, United Kingdom, 2Division of Anaesthesia, Department of Medicine, University of Cambridge, Cambridge, United Kingdom, 3Universitair Ziekenhuis Antwerpen, Antwerp, Belgium, 4MRC Cognition and Brain Sciences Unit, University of Cambridge, Cambridge, United Kingdom
Synopsis
This study compares the impact of voxel-wise versus region-wise harmonisation of diffusion-weighted imaging (DWI) signal via Z-scoring and ComBat. Both approaches and algorithms were shown equally effective in significantly reducing the variation in regionally observed FA and MD in a multi-acquisition DWI dataset.
Introduction
The sensitivity of diffusion-weighted imaging (DWI) to acquisition parameters1,2,3 is hindering the direct comparison of diffusion characteristics across multi-centre databases with varying DWI protocols. Various DWI harmonisation methods have been suggested as solution4,5, but there is no guidance whether to harmonise diffusion signal voxel- or region-wise. This study compares both approaches using Z-Scoring and ComBat.6Methods
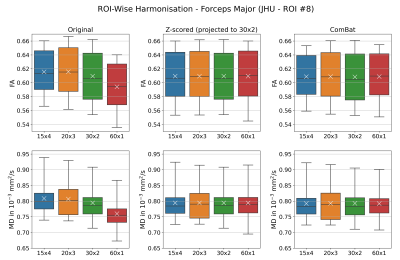
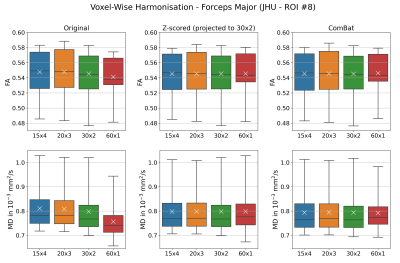
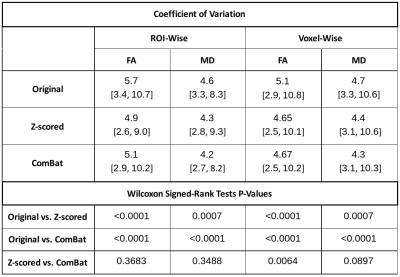
Four DWI protocols with identical acquisition parameters (Siemens Trio 3T, TR = 8000 ms, TE = 93 ms, voxels: 2x2x2 mm3), but different number of b-values were used to image 16 healthy subjects (nine female, seven male, age = 25.8 ± 5.4 years). The overall angular resolution was consistent, but directions were distributed over one to four shells. This included four shells with each 15 directions (15x4): b = 300, 600, 900, 1200 s/mm2, three shells with each 20 directions (20x3): b = 400, 800, 1200 s/mm2, two shells with each 30 directions (30x2): b = 600, 1200 s/mm2 and a single shell with 60 directions (60x1): b = 1200 s/mm2. The 13 non-diffusion weighted volumes (b0) were evenly collected between volumes with different diffusion-sensitisation (single-shell: all b0 collected at the beginning). DWI were processed as follows: Denoising via MPPCA7, Gibbs ringing removal8,9 eddy current and head motion correction10, and bias-field correction.11 Fractional anisotropy (FA) and mean diffusivity (MD) maps were computed with weighted least-squares tensor fitting.12 A study-specific template was created13 via tensor registration14 to spatially normalise all scans. All individual FA maps and the template FA map were non-linearly registered15 to the JHU-ICBM FA atlas.16 Its fibre tract probability maps were backprojected to native space and study-template (linear interpolation) and thresholded at 25% to compute weighted means of FA and MD maps for all 20 regions of interest (ROIs). Diffusion signal was harmonised via Z-scoring and ComBat. The former involved first standard scaling data for each acquisition scheme separately by subtracting the mean signal and divide by its standard deviation. Then, normalised signal was projected to the 30x2 scheme by reversing the standard scaling with mean and standard deviation of the 30x2 data. To include data correspondence across schemes, subject identifiers were used as covariates for ComBat. Both harmonisation methods were applied on mean ROI values extracted in native scan space (ROI-wise) and on voxel intensities in template space (voxel-wise). Differences in FA or MD were assessed region-wise across all four schemes before and after harmonisation (Friedman tests). P-values were corrected for false discovery rate (FDR; Benjamini-Hochberg, family-wise error rate: 0.05). Coefficients of variation (CV) were computed as the ratio of standard deviation ($$$\sigma$$$) and mean ($$$\mu$$$) of the regional observations ($$$CV=\sigma/\mu\times100\%$$$) both in native and template space. For each ROI, the CVs were derived for the combined multi-acquisition dataset before and after harmonisation, and these CVs were compared to examine the impact of harmonisation (Wilcoxon signed-rank tests).Results
Diffusion metrics showed significant differences between acquisition schemes in native space (Friedman tests: FA: pFDR < 0.0005, MD: pFDR < 0.0002) and study-template space (Friedman tests: FA: pFDR < 0.0006, MD: pFDR < 0.0004). Only MD in the left cingulum was statistically indistinguishable in template space (template: pFDR = 0.0887, native: pFDR = 0.0471). When applied to mean ROI values, Z-scoring (all Friedman tests: FA: pFDR > 0.9940, MD: pFDR > 0.9940) and ComBat (all Friedman tests: FA: pFDR > 0.9850, MD: pFDR > 0.9730) both successfully eliminate statistical differences between schemes. Similar results were obtained for voxel-wise harmonisation (Friedman tests: Z-scoring FA: pFDR > 0.9940 and MD: pFDR > 0.9999; Combat FA: pFDR > 0.9040 and MD: pFDR > 0.9730). Figure 1 and 2 show an example of FA and MD in the forceps major (ROI #8) before and after harmonisation. Variation in regional mean FA measured on spatially normalised scans was on average lower (5.1%) then when measured in native space (5.7%). Overall, regional MD variation is on average lower (4.2% - 4.7%) than that for FA (4.7% - 5.7%) before and after harmonisation. Both harmonisation algorithms reduced variation in diffusion metrics, regardless whether they were applied on a ROI or voxel level (all Wilcoxon: p < 0.001). Overall, Z-scoring and ComBat performed equally well with mostly no statistical differences observed (Wilcoxon p > 0.089). Voxel-wise harmonisation of FA was marginally better with Z-scoring than ComBat (Wilcoxon: p = 0.0064). ROI-wise harmonisation of FA seemed minimally more beneficial than voxel-wise harmonisation (Table 1).Discussion & Conclusion
The limitations of ComBat have previously been reported for differently processed DWI data.17 Our experiments showed the capability of Z-scoring and Combat harmonisation to reduce FA and MD differences across different DWI acquisitions. Both methods include additive and multiplicative components for signal harmonisation, which may explain their overall similar performance. A regional or voxel-wise level application had little effect on the harmonisation success. Of note, FA variation was lower on scans in template space compared to native-space, which could be a result of image smoothing due to spatial normalisation. We conclude that both Z-scoring and ComBat can be equally helpful to minimise variations in FA and MD, but acknowledge that this might be more challenging for less controlled datasets.Acknowledgements
No acknowledgement found.References
1. Correia, Marta Morgado, Thomas A. Carpenter, and Guy B. Williams. "Looking for the optimal DTI acquisition scheme given a maximum scan time: are more b-values a waste of time?." Magnetic resonance imaging 27.2 (2009): 163-175.
2. Papinutto, Nico Dario, Francesca Maule, and Jorge Jovicich. "Reproducibility and biases in high field brain diffusion MRI: An evaluation of acquisition and analysis variables." Magnetic resonance imaging 31.6 (2013): 827-839.
3. Zhan, Liang, et al. "How does angular resolution affect diffusion imaging measures?." neuroimage 49.2 (2010): 1357-1371.
4. Tax, Chantal MW, et al. "Cross-scanner and cross-protocol diffusion MRI data harmonisation: A benchmark database and evaluation of algorithms." NeuroImage 195 (2019): 285-299.
5. Pinto, Maíra Siqueira, et al. "Harmonization of Brain Diffusion MRI: Concepts and Methods." Frontiers in Neuroscience 14 (2020).
6. Fortin, Jean-Philippe, et al. "Harmonization of multi-site diffusion tensor imaging data." Neuroimage 161 (2017): 149-170.
7. Veraart, Jelle, Els Fieremans, and Dmitry S. Novikov. "Diffusion MRI noise mapping using random matrix theory." Magnetic resonance in medicine 76.5 (2016): 1582-1593.
8. Kellner, Elias, et al. "Gibbs‐ringing artifact removal based on local subvoxel‐shifts." Magnetic resonance in medicine 76.5 (2016): 1574-1581.
9. Neto Henriques, Rafael. Advanced Methods for Diffusion MRI Data Analysis and their Application to the Healthy Ageing Brain. Diss. University of Cambridge, 2018.
10. Andersson, Jesper LR, and Stamatios N. Sotiropoulos. "An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging." Neuroimage 125 (2016): 1063-1078.
11. Jeurissen, Ben, et al. "Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data." NeuroImage 103 (2014): 411-426.
12. Smith, Stephen M., et al. "Advances in functional and structural MR image analysis and implementation as FSL." Neuroimage 23 (2004): S208-S219.
13. Zhang, Hui, et al. "Unbiased white matter atlas construction using diffusion tensor images." International conference on medical image computing and computer-assisted intervention. Springer, Berlin, Heidelberg, 2007.
14. Zhang, Hui, et al. "Deformable registration of diffusion tensor MR images with explicit orientation optimization." Medical image analysis 10.5 (2006): 764-785.
15. Avants, Brian B., Nick Tustison, and Gang Song. "Advanced normalization tools (ANTS)." Insight j 2.365 (2009): 1-35.
16. Mori, Susumu, et al. MRI atlas of human white matter. Elsevier, 2005.
17. Cetin-Karayumak, Suheyla, et al. "Exploring the limits of ComBat method for multi-site diffusion MRI harmonization." bioRxiv (2020).
Figures