2860

Towards direct neuronal-current MRI: a novel statistical processing technique for measurements in the presence of system imperfections.
Chiara Coletti1, Sebastian Domsch1, Frans Vos1, and Sebastian Weingärtner1
1Imaging Physics, TU Delft, Delft, Netherlands

Synopsis

Functional imaging based on detection of neuronal currents using spin-lock prepared MRI may overcome limitations inherent to haemodynamic fMRI with BOLD. However, in-vivo application is hindered by system imperfections. In this work, the effects of B0 and B1+ inhomogeneities and background noise on neuro-current MRI signals are quantified. Furthermore, a new statistical data-processing technique based on the analysis of signal variability, SVarM, is proposed for neuro-current MRI time series. SVarM achieves overall higher sensitivity than existing data-processing methods and is shown to be more robust in the presence of system imperfections.

Introduction

Functional Magnetic Resonance Imaging (fMRI) is traditionally based on Blood-Oxygen-Level-Dependent (BOLD) contrast1. However, BOLD fMRI only provides an indirect measure of neuronal activity and suffers from the temporal delay introduced by the haemodynamic response2.
Direct detection of magnetic fields elicited by neuronal activity using MRI has been a long standing research goal, due to its potential to overcome BOLD fMRI limitations and enable the investigation of brain activity with high temporal resolution and specificity3-5. Recent studies have demonstrated that the MRI signal can be sensitized to oscillating magnetic fields generated by concerted voltage fluctuations, so-called Local Field Potentials (LFPs)6, using spin-lock preparations7-9. At present, the applicability of spin-lock sequences in-vivo remains hindered by the presence of system imperfections10. Moreover, conventional fMRI data processing techniques are not suited for the analysis of neuro-current MRI signals, encoding neuronal activity in the signal variance9.
This work investigates the influence of B0 and B1+ imperfections on state-of-the-art spin-lock sequences for neuro-current MRI using Bloch simulations. A new data-processing technique, Statistical Variance Mapping (SVarM), is proposed to perform statistical analysis of neuro-current MRI time series. Compared to the existing data-processing technique, SVarM shows higher resilience to B0/B1+ fields inhomogeneities and background noise.

Methods

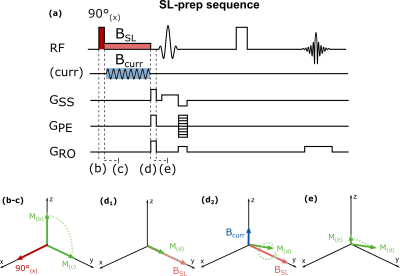
The spin-lock sequence used for neuro-current MRI in this study is depicted in Fig. 19. Bloch equations were used to simulate the magnetization evolution during the spin-lock preparation for different levels of B0 and B1+ inhomogeneities (±200Hz off-resonances, ±100% B1+, for B0=3T, BCURR=200nT, fCURR=100Hz, tSL=100ms, T1ρ=78ms11).
Based on the results of Bloch simulations, synthetic neuro-current MRI time series were simulated for an entire brain volume (1x1x3mm3 resolution). A block-design paradigm consisting of 10 bilateral finger-tapping periods interleaved with 10 rest periods was used (duration=13.5s each)12. BOLD response, identified through Statistical Parametric Mapping (SPM) first level analysis13, was used as a proxy for LFPs activation. Neuro-current time series were modulated to account for phase differences between the spin-lock and neuro-currents fields. B0 and B1+ inhomogeneities were extracted from representative B0/B1+ maps. Measurement noise was added to the time series.
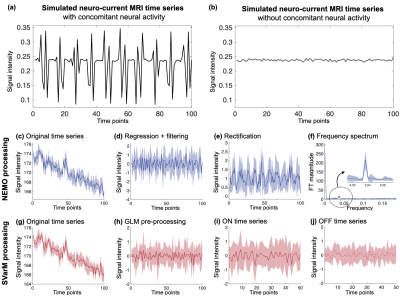
Neuro-current time courses in presence of neuronal activation (Fig. 2a) depict constant mean with higher variance during activation phases, in contrast to the boxcar activation patterns of BOLD fMRI. Thus, a tailored statistical data-processing technique, SVarM, is introduced and compared to the existing procedure, termed Neuro-Electric-Magnetic Oscillations (NEMO) processing9. In SVarM, first, a GLM was used to remove physiological motion confounds and other low frequency artifacts from the neuro-current signal, similarly to SPM, but without a regressor encoding BOLD activation (Fig. 2h). Next, time series data were pooled into two groups, corresponding to signals acquired during active and rest blocks (Fig. 2i-j). Levene’s test with the null hypothesis of equal variability was used for non-paired statistical variance testing across the two groups in order to detect significant differences in variability between active and rest periods.
The two processing techniques were tested on the generated synthetic neuro-current dataset. Resulting activation maps were evaluated with respect to the reference BOLD activation using Dice Score (DS=2∗TP/(2∗TP+FP+FN)) and Surviving Pixels Ratio (SPR=TP+FP) coefficients, averaged over 10 runs for each experimental condition. Statistical significance of the results was tested with a two-way ANOVA analysis.

Results

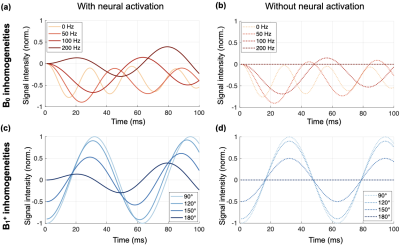
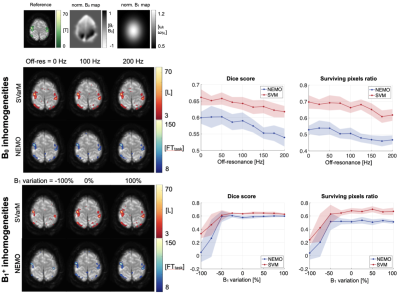
Simulation results depict the longitudinal magnetization evolution during the spin-lock preparation and the trajectory modification in presence of B0 and B1+ inhomogeneities (Fig. 3). Substantial variation of sensitivity can be seen for ±200Hz of off-resonances and ±100% variations in B1+, resulting in ±100% oscillations from the original signal intensity.
Fig. 4 presents outcome activation maps obtained with SVarM and NEMO processing for different levels of B0 and B1+ fields inhomogeneities, along with corresponding DS and SPR plots. An average 6.31% DS increase, and +16.65% SPR increase, is obtained with SVarM compared with NEMO across the off-resonances range (p<0.01). Moreover, SVarM has only minor sensitivity loss in case of severe (<-50%) B1+ variations (p<0.02).
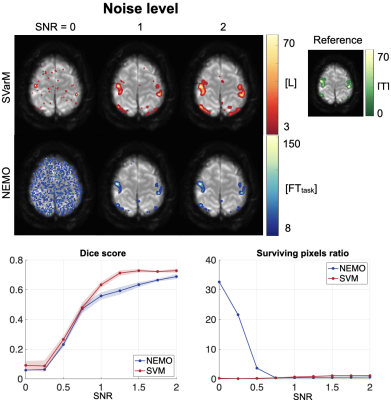
Fig. 5 shows the analysis of the two processing techniques with increasing noise levels. SVarM achieves higher rejection of false positives for low signal-to-noise ratios (SPR: 62.34±0.74% SVarM, 3261.70±5.48% NEMO, p<0.01).

Discussion

This work studies the effects of system imperfections on neuro-current MRI signals. High susceptibility to B1+ inhomogeneities and SNR was observed. Nonetheless, the proposed statistical analysis, SVarM, was found to alleviate the effects of imperfections and increase overall sensitivity with respect to NEMO processing.
SVarM is based on the variance analysis of time series, since neuro-current MRI activation is encoded in the signal variability, rather than signal mean shifts, as in BOLD MRI. SVarM is easily applied to a block-design paradigm, which allows for data splitting. Extension to other experimental protocols will be subject of future work.
Compared to NEMO processing, SVarM achieved an increase in detection sensitivity, without loss of specificity. However, neuro-current MRI sensitivity remains inherently lower than BOLD MRI. Designing more robust pulse-sequences remains a key factor for the effective application of this contrast mechanism.

Conclusions

The results of this study indicate that neuro-current MRI is substantially compromised by the presence of system imperfections. The combination of specific data-processing techniques and advanced sequence design is necessary to fully enable the use of neuro-currents MRI for direct detection of neuronal activity.

Acknowledgements

S.W. acknowledges funding from the 4TU Precision Medicine program, a NWO Start-up STU.019.024 and ZonMW OffRoad 04510011910073.

References

[1] Ogawa, S., Lee, T. M. et al., Brain magnetic resonance imaging with contrast dependent on blood oxygenation., Proc. Nat. Acad. Sc. U. S. A., 87(24): 9868–9872, 1990.

[2] Menon, R. S. and Kim, S. G., Spatial and temporal limits in cognitive neuroimaging with fMRI., Tr. Cogn. Sc., 3(6): 207–216, 1999.

[3] Scott, G.C., Joy, M.L.G. et al., Rotating Frame RF Current Density Imaging., Magn. Reson. Med., 33: 355-369, 1995.

[4] Petridou, N., Plenz, D. et al., Direct magnetic resonance detection of neuronal electrical activity., Proc. Nat. Acad. Sc., 103(43): 16015–16020, 2006.

[5] Kraus, R.H., Jr, Volegov, P. et al., Toward direct neural current imaging by resonant mechanisms at ultra-low field., NeuroImage, 39: 310–317., 2008.

[6] Logothetis, N., Pauls, J. et al., Neurophysiological investigation of the basis of the fMRI signal., Nature 412: 150–157, 2001.

[7] Witzel, T., Lin, F. H., Rosen, B. R. and Wald, L. L., Stimulus-induced Rotary Saturation (SIRS): a potential method for the detection of neuronal currents with MRI., NeuroImage, 42(4): 1357–1365, 2008.

[8] Halpern-Manners, N. W., Bajaj, V. S., Teisseyre, T. Z. and Pines, A., Magnetic resonance imaging of oscillating electrical currents., Proc. Nat. Acad. of Sc. U. S. A., 107(19): 8519–8524, 2010.

[9] Truong,T.K.,Roberts,K.C.,Woldorff,M.G.andSong,A.W.,Toward direct MRI of neuro-electro-magnetic oscillations in the human brain., Magn. Res. Med., 81(6): 3462–3475, 2019.

[10] Chen W., Errors in quantitative T1rho imaging and the correction methods., Quant. Im. Med. Surg., 5(4): 583–591, 2015.

[11] Watts, R., Andrews, T., Hipko, S., Gonyea, J.V. and Filippi, C.G., In vivo whole-brain T1-rho mapping across adulthood: Normative values and age dependence., J. Magn. Reson. Imag., 40: 376-382, 1999.

[12] Domsch, S., Zapp, J., Schad, L. R., Nees, F., Hill, H., Hermann, D., Mann, K. and Vollstadt-Klein, S., Optimized protocol for high resolution functional magnetic resonance imaging at 3T using single-shot echo planar imaging., Journ. Neurosc. Meth., 239: 170–182, 2015.

[13] Friston, K.J., Holmes, A.P., Worsley, K.J., Poline, J.-P., Frith, C.D. and Frackowiak, R.S.J, Statistical parametric maps in functional imaging: A general linear approach., Hum. Brain Mapp., 2: 189-210, 1994.

Figures

Spin-lock sequence diagram (a), where the amplitude of the spin-lock field is tuned to the oscillating neuro-magnetic fields frequency ωCURR to induce resonance condition. The spin-lock preparation consists of excitation (b-c), application of the spin-lock pulse without (d1) and with (d2) the concomitant neuro-current field action, gradient spoiling (e). The effect of neuro-currents is encoded in the residual longitudinal magnetization, after spoiling.

Simulated neuro-current time series with (a) or without (b) concomitant neural activation. Time courses (mean ± std) after each step of data processing. NEMO consists of a regression and high-pass filtering step to remove low frequency confounds (d), a rectification step converting variance differences in mean shifts (e) and extraction of the peak magnitude in the frequency spectrum at the task frequency (f). SVarM uses GLM regression to remove low frequency confounds (h), then pools the data into ON and OFF groups and tests the difference in their variance with Levene’s test (i-j).

Temporal evolution of longitudinal magnetization during the spin-lock pulse application, simulated with (a,c) or without (b,d) concomitant neural activation. Fig.3a-b represent the magnetization for different values of off-resonances (imperfect B0). Fig3c-d depict the magnetization for different values of effective flip angle (imperfect B1+).

Representative activation maps for the two processing methods, NEMO and SVarM, for different levels of B0 and B1+ inhomogeneities. On the right, corresponding plots of Dice score and surviving pixels ration (mean ± std). On the top, ground truth activation map, obtained from BOLD fMRI experiments, and representative B0 and B1+ field maps.

Representative activation maps for the two processing methods, NEMO and SVarM, for different levels of signal-to-noise ratio. On the bottom, corresponding plots of Dice score and surviving pixels ration (mean±std). On the right, ground truth activation map, obtained from BOLD fMRI experiments.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)
2860