Introduction

There is an increasing need for realistic microstructural substrates when simulating diffusion tensor cardiovascular magnetic resonance (DT-CMR). Recent work [3] found a significant difference in diffusion tensor parameters measured in substrates constructed from a regular arrangement of cuboids compared to one constructed directly from histology. The largest differences were found in the orientation of the second eigenvector (E2A) and the fractional anisotropy (FA) computed from the simulated signal. This can be attributed to the way cardiomyocytes are grouped into functional groups called sheetlets, which in turn are separated by shear layers.

A common approach to construct the substrate is by manual segmentation [1], which can be time consuming especially when large parameter studies are to be carried out. To date, no automatic method exists to synthesise virtual cardiac tissue. In the brain, AxonPacking [2] has proven a useful software package to solve the packing problem of axonal cells by representing them as 2-dimensional, circular objects. Axons are, however, much simpler geometrically than cardiomyocytes and white matter does not have the secondary sheetlet structure perpendicular to the long axis of the cells that is observed in the myocardium.

Methods

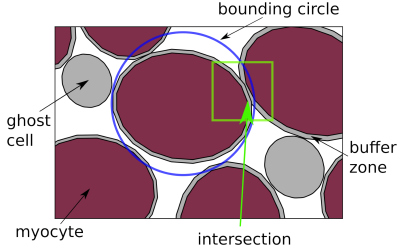
We present a method to rigidly pack polygons of arbitrary shape into a dense arrangement inside an arbitrary shaped target region. The objects are randomly seeded on points of a grid which is larger than but has approximately the same aspect ratio as the bounding box of the target region. Myocytes are represented by ellipses, drawing their area and aspect ratio from distributions matching those found in segmented histology images. Additionally, we allocate a certain number of “ghost cells”. These objects participate in the packing as normal but are removed at the end of the simulation. By correctly choosing their (smaller) size and quantity, pockets of extra-cellular space (ECS) can be simulated.
Every time step, all non-overlapping objects converge towards the origin (centre of the target region) at a pre-determined attraction velocity $$$U_\text{att}$$$. Objects that overlap with other objects are repelled with $$$U_\text{rep}$$$ in the direction of the resultant vector, $$$\vec{v}_\text{res}$$$, which is the sum of the pairwise difference of positions. We set $$$U_\text{rep}$$$ to be twice $$$U_\text{att}$$$. After an initially large magnitude of $$$U_\text{att}$$$, which helps accelerate convergence in an initially sparse domain, we reduce the attraction speed. Once the extra-cellular volume fraction (ECV) in the target region has stabilised, the simulation is terminated. We perform a few additional time steps with $$$U_\text{att} = 0$$$ and a small value for $$$U_\text{rep}$$$ to “wiggle” all objects into place. Figure 1 illustrates the algorithm.

Each cell is given a small buffer zone around its outer boundary for numerical reasons, which is discarded at the end of the simulation. This prevents the actual objects from overlapping in the final arrangement. To accelerate the computationally expensive calculation of the intersection of polygons, we construct bounding circles around each object and use these for fast rejection decisions via an improved version of the pairwise distance matrix [2].

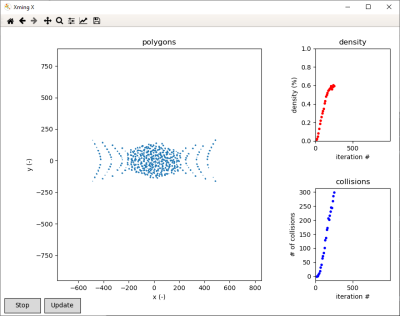
The software is written in Python, relying extensively on the NumPy and shapely modules. It is open-sourced and available on GitHub [4]. Convergence can be monitored via a graphical user interface (GUI). For batch simulations, we also provide a command line interface (CLI). Figure 2 shows an example simulation observed through the GUI.

Results

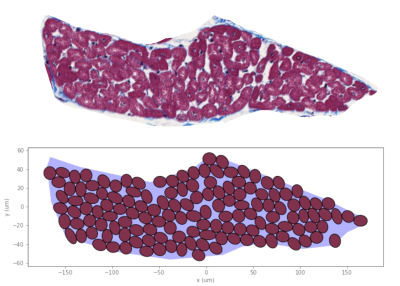
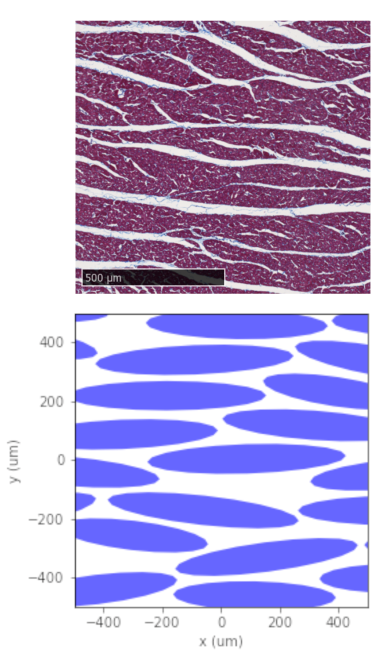
Figure 3 compares the packing of a sheetlet with a histological image of the same sheetlet. Only myocytes that overlap with the sheetlet polygon by at least 70% are accepted. Both the number of cells (130 for histology vs 140 for synthetic) and the overall cell density (76% vs 75%) are in good agreement. Visually, the distribution of extra-cellular space within the sheetlet is comparable.

Figure 4 shows the result of packing a domain with sheetlet-like objects, then packing each of them with myocytes. The domain is cropped to an imaging voxel size of 1x1mm².

The simulation time for packing the sheetlet in Figure 3, using a single core (2.4GHz) on a modern workstation, was 225s. The sheetlets inside the voxel on the other hand can be packed in seconds, owing to the low number of objects involved. The subsequent packing of each sheetlet with myocytes can be performed in parallel using the CLI and 36 cores on the same workstation, with runtimes not exceeding a few minutes.

Discussion

The presented algorithm allows for packing of arbitrary shapes into tight arrangements. This improves upon [2], where packing was confined to circular cylinders. While the latter is computationally more efficient, it fails to represent real cardiomyocyte shapes which are circular only in the idealised case. The addition of “ghost cells” enables irregular gaps between cell objects, which generates a more realistic substrate.

Conclusion

The presented tool forms part of a pipeline that allows for easy synthesis of DT-CMR data, going from the statistics of cell and sheetlet sizes and shapes to a simulation-ready substrate. In the future, this 2D packing may be extended to packing the sheetlet structures in 3D. Additionally, we plan to investigate the use of deformation and rotation of the polygons during packing.

Acknowledgements

This work was funded by British Heart Foundation Grant RG/19/1/34160 and British Heart Foundation Centre of Research Excellence Grant RE/13/4/30184.