2848
Implications of a constant tissue-trace constraint on the two-compartment free water model
Jordan A. Chad1,2, Ofer Pasternak3, and J. Jean Chen1,2
1Department of Medical Biophysics, University of Toronto, Toronto, ON, Canada, 2Rotman Research Institute, Baycrest Health Sciences, Toronto, ON, Canada, 3Brigham and Women's Hospital, Harvard Medical School, Boston, MA, United States
1Department of Medical Biophysics, University of Toronto, Toronto, ON, Canada, 2Rotman Research Institute, Baycrest Health Sciences, Toronto, ON, Canada, 3Brigham and Women's Hospital, Harvard Medical School, Boston, MA, United States
Synopsis
It has been found that when the single-shell two-compartment free water fit is initialized with a constant trace of the tissue tensor, the final results maintain this constant tissue-trace. It is therefore important to understand the implications of the constant tissue-trace constraint in order to interpret the results of single-shell free water studies. Here we demonstrate that this constraint results in allotting all variation in isotropic diffusivity to the free water compartment while the tissue tensor is unaffected by isotropic variations. It is further shown that the isotropic compartment is more linearly aligned with quadratic variations in diffusivity.
Introduction
The two-compartment free-water model in diffusion MRI, which is seeing wide adoption, is given by1$$s_{\textrm{FW}} = \textrm{s}_0 \big[(1-f)e^{-b\hat{\mathbf{q}}^\textrm{T}\mathbf{D}\hat{\mathbf{q}}} + fe^{-bd} \big] \quad \textrm{(1)}$$
where d=3x10-3mm2/s is the diffusivity of free water at body temperature, and the free parameters are the free water fraction f and the tissue diffusion tensor D. Since fitting two compartments to single-shell data is ill-posed, a regularization scheme has been proposed that constrains D to vary smoothly between neighboring voxels.1 However, if the single-shell fit is initialized with a constant trace of D across all voxels, the initialization is already smooth, so the final results often maintain this constant tissue-trace.2-4 It is therefore important to understand the implications of a two-compartment model with a constant tissue-trace in order to properly interpret the results of single-shell free-water studies that are initialized with a constant tissue-trace.
Theory
The two compartment model with a constant tissue-trace is derived by first computing the overall mean diffusivity (MD), and then setting$$e^{-b \textrm{MD}} = (1-f)e^{-b\textrm{MDt}} + fe^{-bd} \quad \textrm{(2)}$$
where the tissue MD (i.e., MDt) is set to a fixed value, e.g., MDt =0.6μm2/ms. Therefore, the free water fraction is related to the mean diffusivity by
$$f = -\textrm{A} e^{-b\textrm{MD}} + \textrm{C} \quad \textrm{(3)}$$
where A and C are constants defined as:
$$\textrm{A} = \frac{1}{e^{-b\textrm{MDt}}-e^{-bd}} \quad \textrm{(4)}$$ and $$\textrm{C} = \frac{e^{-b\textrm{MDt}}}{e^{-b\textrm{MDt}}-e^{-bd}} \quad \textrm{(5)}$$
In other words, fixing MDt allots isotropic variation (i.e., variation in MD) as variation in f via a nonlinear relationship defined in Eq. 3. The eigenvalues of the tissue tensor λFW-DTI = {λ1,2,3} are then given by
$$\boldsymbol{\lambda}^{\textrm{FW-DTI}} = \boldsymbol{\lambda}^{\textrm{DTI}} - \frac{1}{b}\textrm{ln}\bigg( \frac{1 - f e^{-b(d-\boldsymbol{\lambda}^{\textrm{DTI}})}} {1-f} \bigg) \quad \textrm{(6)}$$
The second term on the right effectively holds the mean of the tissue tensor eigenvalues constant such that the tissue tensor and its fractional anisotropy are unaffected by variation in isotropic diffusion. Instead, variation in fractional anisotropy of the tissue tensor is specific to variation in anisotropy between the eigenvalues.
Methods
To understand the implication of fixing MDt on age modeling, DTI metrics derived from the tissue compartment were simulated for various “ages” by computing the eigenvalues of the tissue tensor λFW-DTI from Eq. 6 using linear models for λDTI in line with those widely used for modeling aging white matter:5$$ \lambda_1^{\textrm{DTI}}(x) = \lambda_1^{\textrm{DTI}}(40) + \alpha_1 (x-40) \quad \textrm{(7)}$$
$$ \lambda_{2,3}^{\textrm{DTI}}(x) = \lambda_{2,3}^{\textrm{DTI}}(40) + \beta_1 (x-40) \quad \textrm{(8)}$$
with α1=0.001, β1=0.002, and λDTI(40) = [1.6,0.5,0.3]μm2/ms. Since Eqs. 7-8 are generally considered to be linear approximations of quadratic functions,5 quadratic models were further studied
$$ \lambda_1^{\textrm{DTI}}(x) = \lambda_1^{\textrm{DTI}}(40) + \alpha_2 (x-40)^2 \quad \textrm{(9)}$$
$$ \lambda_{2,3}^{\textrm{DTI}}(x) = \lambda_{2,3}^{\textrm{DTI}}(40) + \beta_2 (x-40)^2 \quad \textrm{(10)}$$
with α2=0.0000625, β2=0.00015625, and λDTI(40) = [1.6,0.5,0.3]μm2/ms. The linear correlation coefficient of age with both MD = ⅓ΣλiDTI and the corresponding f (Eq. 3) were compared.
Results
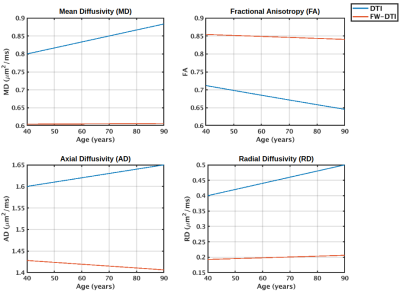
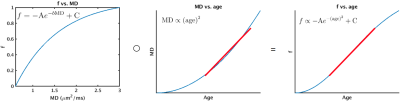
Figure 1 displays age associations of metrics derived from the tissue tensor with fixed trace (Eq. 6), and from conventional DTI. These results are consistent with reported aging findings using the full single-shell model fit.6 The other reported aging finding is that f exhibited stronger linear age associations than MD. This can be explained if the variation in MD with age better follows a quadratic distribution, as Figure 2 demonstrates that Eq. 3 approximately linearizes this distribution. For ages 40-80, using models Eq. 9-10, the correlation coefficient of MD with age is r=0.96 and the correlation coefficient of f with age is r=0.97.Discussion
This work demonstrates that the two-compartment free water model fit to single-shell data distinguishes variation in isotropic and anisotropic diffusion when implementing a constant tissue-trace constraint. The isotropic compartment can reflect variation in extracellular processes such as enlarged extracellular space and/or increased inflammation. To increase the specificity of the isotropic compartment to free water, multi-shell data would likely be beneficial, because a multi-shell fit can move beyond the constant tissue-trace initialization. That said, the increased sensitivity of the single-shell fit to biological processes has largely derived from including all isotropic diffusivity in a single parameter.4 As this work suggests, the linear sensitivity of the free water compartment to biological processes can be especially enhanced by the nonlinear relationship between free water and tissue trace (Eq. 3). Overall, this study highlights the importance of understanding the fixed trace initialization in order to properly interpret the results of single-shell free water studies.Acknowledgements
We thank CIHR, NSERC and NIH for financial support.References
1. Pasternak O et al (2009) Free water elimination and mapping from diffusion MRI. Magn Reson Med 62(3):717-730.
2. Golub M, Henriques RN, Nunes RG (2020) Free‐water DTI estimates from single b‐value data might seem plausible but must be interpreted with care. Magn Reson Med doi:10.1002/mrm.28599
3. Parker D et al (2020) Freewater estimatoR using iNtErpolated iniTialization (FERNET): Characterizing peritumoral edema using clinically feasible diffusion MRI data. PLoS ONE 15:e0233645
4. Horovitz SG et al (2019) Biological interpretation of the “free water” increases in the substantia nigra of PD patients. OHBM 2019 pW810
5. Lebel C et al (2012) Diffusion tensor imaging of white matter tract evolution over the lifespan. Neuroimage 60:340-352.
6. Chad JA et al (2018) Re-examining age-related differences in white matter microstructure with free-water corrected diffusion tensor imaging. Neurobiol Aging 71:161-170.
Figures
Figure 1. Reproduction of the “tissue compartment” results of a single-shell free-water study of aging white matter, simulated using the constant tissue-trace constraint. Metrics derived from the tissue compartment, as per Eq. 6, represent variation in the shape of the tissue tensor while the size remains constant, since all isotropic variations are allotted to the free water compartment. For a biological interpretation of these results, see ref. 6.
Figure 2. Reproduction of the “free water compartment” results of a single-shell free-water study of aging white matter, simulated using the constant tissue-trace constraint. The constant tissue-trace relationship between f and MD (Eq. 3) is nonlinear, so the linear correlation coefficients exhibited by f and MD differ. If MD better follows a quadratic distribution, as is thought to be the case in aging, f follows a distribution that can be better approximated by a line.