2845

A direct link between the DKI model and the sub-diffusion process

Qianqian Yang¹ and Viktor Vegh^2,3
¹Queensland University of Technology, Brisbane, Australia, ²The University of Queensland, Brisbane, Australia, ³Centre for Innovation in Biomedical Imaging Technology, Brisbane, Australia

Synopsis

Diffusion kurtosis imaging (DKI) is an important tool in tissue microstructure studies. The DKI formula for diffusion-weighted MRI signal decay arises through a high order expansion, and the kurtosis has been shown to be sensitive to changes in tissue microstructure. Interestingly, the kurtosis formula describes deviation away from mono-exponential signal decay, like that previously described for anomalous diffusion. Here, we make a link between anomalous sub-diffusion in tissue and diffusion kurtosis. This direct link enables the apparent diffusivity and kurtosis to be computed easily from the sub-diffusion model parameters, leading to superior white-grey matter contrast compared with standard DKI parameters.

Introduction

Many studies have shown the diffusion signal as a function of b-value to deviate away from mono-exponential decay ^e.g.,1-14. Such diffusional non-Gaussianity is a consequence of tissue microstructure, leading to hindered and restricted diffusion in MRI voxels. To quantify the degree of non-Gaussianity of water diffusion, Jensen et al.¹⁴ proposed the diffusion kurtosis imaging (DKI) to estimate excess kurtosis, an indicator of water molecule motion away from Gaussian diffusion. However, limitations of DKI include a limit on the maximum b-value (up to about 2500s/mm²) which can be used to fit the model and how robustly model parameters can be extracted by fitting a model to MRI data. In parallel, models based on fractional calculus theory have also been proposed to capture the non-Gaussian anomalous diffusion behaviour^1-13. It has been shown that anomalous diffusion models, such as super-diffusion^1,², sub-diffusion^5,12, quasi-diffusion¹³, continuous time random walk⁶^,8,9, fractional Bloch-Torrey^3,^4,11 and fractional motion^7,10 models, are able to better fit the diffusion-weighted MRI signal with large b-values than the mono-exponential model, and potentially provide a link with tissue microstructure variations through anomalous diffusion model parameters. In this study we aimed to investigate how a connection can be made between DKI and anomalous diffusion with a particular focus on sub-diffusion, and how kurtosis can be computed from the sub-diffusion model parameter.

Methods

Theory
We now provide the derivation which links the DKI formulation with the sub-diffusion model. The sub-diffusion model takes the form:
$$S/S_0=E_\beta(-bD_{SUB}), 0<\beta\leq1, ~~~~~~ (1)$$
where $$$S_0$$$ is the signal intensity when $$$b=0$$$, $$$D_{SUB}$$$ is the apparent diffusivity of tissue in units of mm²/s , $$$\beta$$$ is the sub-diffusion exponent, and $$$E_\beta(z)=\sum^\infty _{k=0}\frac{z^k}{\Gamma(1+\beta k)}$$$ is the Mittag-Leffler function. Since the parameters in the sub-diffusion model are real and positive, we are dealing with a real-valued Mittag-Leffler function. This allow us to take natural logarithm of (1) and obtain:
$$log(S/S_0) = log(E_\beta(-bD_{SUB})). ~~~~~~~~(2) $$
Now taking Taylor series expansion at $$$b=0$$$ gives:
$$ log(E_\beta(-bD_{SUB})) = -\frac{bD_{SUB}}{\Gamma(1+\beta)} + \left(\,\frac{1}{\Gamma(1+2\beta)}-\frac{1}{2\Gamma(1+\beta)^2}\right)\, b^2D_{SUB}^2 + O(b^3). ~~~~~~~(3) $$
By letting
$$ D^*=\frac{D_{SUB}}{\Gamma(1+\beta)}, ~~~~~~~(4)$$
Eq.(3) can be expressed in the DKI form:
$$ log(E_\beta(-bD_{SUB})) = -bD^*+\frac{1}{6}b^2D^{*2} K^*+O(b^3),~~~~~~~(5) $$
with
$$K^*=3\left( 2\frac{\Gamma(1+\beta)^2}{\Gamma(1+2\beta)} - 1 \right), ~~~~~~(6)$$
where $$$0<K^*\leq3$$$ for $$$0<\beta\leq1$$$. Note, when $$$\beta=1$$$, the kurtosis $$$K^*=0$$$, corresponding to the Gaussian case of diffusion. Hence, in view of (5), we can treat the DKI model as a second order approximation of the sub-diffusion model,
$$ S/S_0 = E_\beta(-bD_{SUB}) \approx \exp\left(-bD^*+\frac{1}{6}b^2D^{*2} K^* \right). ~~~~~~~(7)$$
Diffusion-weighted MRI data
Diffusion-weighted MRI data was collected using a 7T Siemens Magnetom research MRI scanner with the following acquisition parameters: TE = 73 ms, isotropic resolution of 1.6 mm³, multiple b-values including 0, 500, 1500, 2500, 3500 s/mm², with a fixed Δ = 31.9 ms and δ = 21.6 ms. A total of 126 acquisitions including six b = 0 datasets were acquired. Directions at each b-value were chosen based on the electrostatic model^15,16. Data were corrected for motion and eddy currents, and trace-weighted images were computed at each b-value (i.e. geometric mean across directions, see Figure 1).

Parameter estimation
The sub-diffusion and DKI models were fitted to the trace-weighted diffusion data ( b=0~3500s/mm²for sub-diffusion model; b=0~2500s/mm² for DKI model) in a voxel-by-voxel manner using MATLAB’s lsqcurvefit function with the trust-region-reflective algorithm. Then, diffusivity and kurtosis were computed according to the sub-diffusion model parameters $$$D_{SUB}$$$ and $$$\beta$$$ as in (4) and (6).

Results

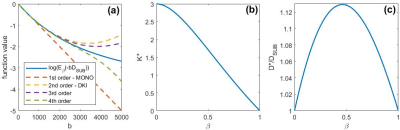
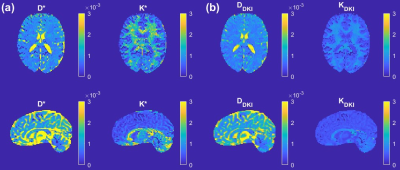
The relationship between sub-diffusion model and its 1st to 4th order approximations including DKI based on Eq. (5) is illustrated in Figure 2(a). The figure shows that the approximations break down from around b = 2000s/mm². Figure 2(b) depicts the relationship between $$$K^*$$$ as defined in Eq. (6) and $$$\beta$$$. Figure 2(c) shows the relationship between $$$D^*/D_{SUB}$$$ as in Eq. (4) and $$$\beta$$$. Figure 3(a) provides maps of the diffusivity, $$$D^*$$$, and kurtosis, $$$K^*$$$, estimated from the sub-diffusion model parameters $$$D_{SUB}$$$ and $$$\beta$$$ according to Eqs. (4) and (6). Figure 3(b) shows the standard DKI maps for the diffusivity, $$$D_{DKI}$$$, and kurtosis, $$$K_{DKI}$$$.

Discussion

Since DKI takes a quadratic form (yellow dashed line in Figure 2(a)), to estimate the kurtosis based on DKI formulation, the maximum of b-value is limited to about b=2500s/mm², a value previously reported to be the limit for the model. However, using the new link between DKI and sub-diffusion formulation, a limitation on the maximum b-value does not have to be set. The diffusivity, $$$D^*$$$, and kurtosis, $$$K^*$$$, can easily be obtained as complementary parameters based on the sub-diffusion model parameters $$$D_{SUB}$$$ and $$$\beta$$$. Furthermore, because a limit on b-value does not have to be imposed for fitting, this new approach of computing kurtosis using the full b-value dataset may provide a more accurate measurement of kurtosis, as the spatially resolved map of $$$K^*$$$ provides a superior grey-white matter contrast in comparison with the traditional DKI metric (compare $$$K^*$$$ and $$$K_{DKI}$$$ in Figure 3).

Conclusion

The mathematically demonstrated link between the DKI and sub-diffusion models provides a new alternative and explicit way of computing kurtosis and apparent diffusivity, with important advantages that the maximum b-value is not limited to 2500s/mm². In the future we will extend this work to computing diffusion and kurtosis tensors based on multiple direction diffusion-weighted data.

Acknowledgements

The authors acknowledge the facilities and scientific and technical assistance of the National Imaging Facility (NIF), a National Collaborative Research Infrastructure Strategy (NCRIS) capability, at the Centre for Advanced Imaging, The University of Queensland. Q. Yang is supported by the Australian Research Council Discovery Early Career Research Award DE150101842. Q. Yang and V. Vegh acknowledge the support of the Australian Research Council Discovery Project Award DP190101889.

References

1. Hall MG, Barrick TR. From diffusion‐weighted MRI to anomalous diffusion imaging. Magnetic Resonance in Medicine. 2008;59(3):447-55.

2. Bennett KM, Schmainda KM, Bennett R, Rowe DB, Lu H, Hyde JS. Characterization of continuously distributed cortical water diffusion rates with a stretched‐exponential model. Magnetic Resonance in Medicine. 2003;50(4):727-34.

3. Zhou XJ, Gao Q, Abdullah O, Magin RL. Studies of anomalous diffusion in the human brain using fractional order calculus. Magnetic Resonance in Medicine. 2010;63(3):562-9.

4. RL Magin, O Abdullah, D Baleanu, XJ Zhou. Anomalous diffusion expressed through fractional order differential operators in the Bloch–Torrey equation. Journal of Magnetic Resonance. 2008;190(2):255-270.

5. Yang Q, Puttick S, Bruce ZC, Day BW, Vegh V. Investigation of changes in anomalous diffusion parameters in a mouse model of brain tumour. In: Bonet-Carne E., Hutter J., Palombo M., Pizzolato M., Sepehrband F., Zhang F. (eds) Computational Diffusion MRI. Mathematics and Visualization. Springer, Cham. https://doi.org/10.1007/978-3-030-52893-5_14

6. Ingo C, Magin RL, Colon‐Perez L, Triplett W, Mareci TH. On random walks and entropy in diffusion‐weighted magnetic resonance imaging studies of neural tissue. Magnetic Resonance in Medicine. 2014;71(2):617-27.

7. Fan Y, Gao JH. Fractional motion model for characterization of anomalous diffusion from NMR signals. Physical Review E. 2015 Jul 6;92(1):012707.

8. Capuani S, Palombo M, Gabrielli A, Orlandi A, Maraviglia B, Pastore FS. Spatio-temporal anomalous diffusion imaging: results in controlled phantoms and in excised human meningiomas. Magnetic resonance imaging. 2013 Apr 1;31(3):359-65.

9. Palombo M, Gabrielli A, De Santis S, Cametti C, Ruocco G, Capuani S. Spatio-temporal anomalous diffusion in heterogeneous media by nuclear magnetic resonance. The Journal of chemical physics. 2011 Jul 21;135(3):034504.

10. Karaman MM, Zhou XJ. A fractional motion diffusion model for a twice‐refocused spin‐echo pulse sequence. NMR in Biomedicine. 2018 Nov;31(11):e3960.

11. Yu Q, Reutens D, O'Brien K, Vegh V. Tissue microstructure features derived from anomalous diffusion measurements in magnetic resonance imaging. Human brain mapping. 2017 Feb;38(2):1068-81.

12. Bueno-Orovio A, Teh I, Schneider JE, Burrage K, Grau V. Anomalous diffusion in cardiac tissue as an index of myocardial microstructure. IEEE transactions on medical imaging. 2016 May 2;35(9):2200-7.

13. TR Barrick, CA Spilling, C Ingo, J Madigan, JD Isaacs, P Rich, TL Jones, RL. Magin, MG. Hall, FA Howe. Quasi-diffusion magnetic resonance imaging (QDI): A fast, high b-value diffusion imaging technique. NeuroImage. 2020;211:116606.

14. Jensen JH, Helpern JA, Ramani, A, Lu H, Kaczynski K. Diffusional kurtosis imaging: The quantification of non‐Gaussian water diffusion by means of magnetic resonance imaging. Magnetic Resonance in Medicine. 2005.53(6):1432-1440.

15. Landman BA, Farrell JA, Jones CK, Smith SA, Prince JL, Mori S. Effects of diffusion weighting schemes on the reproducibility of DTI-derived fractional anisotropy, mean diffusivity, and principal eigenvector measurements at 1.5 T. Neuroimage. 2007 Jul 15;36(4):1123-38.

16. Jones DK, Horsfield MA, Simmons A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine. 1999 Sep;42(3):515-25.

Figures

Figure 1. The trace-weighted images are shown at different b-values (in units of s/mm²) for an axial slice for a young healthy male participant.

Figure 2. Link between sub-diffusion and DKI models: (a) plot of the natural logarithm of the sub-diffusion model and its approximations. Mono-exponential (MONO) and DKI are the first- and second-order approximations of the sub-diffusion model, respectively; (b) relationship between kurtosis $$$K^*$$$ and $$$\beta$$$; (c) relationship between the ratio $$$D^*/D_{SUB}$$$ and $$$\beta$$$. $$$D^*$$$ and $$$K^*$$$ are the diffusivity and kurtosis computed from sub-diffusion model parameters $$$D_{SUB}$$$ and $$$\beta$$$.

Figure 3. Comparison of diffusivity and kurtosis estimated from (a) the sub-diffusion and (b) DKI models. Top row: axial view; bottom row: mid-sagittal view. $$$D^*$$$ and $$$K^*$$$ have been computed based on sub-diffusion model parameters $$$D_{SUB}$$$ and $$$\beta$$$; $$$D_{DKI}$$$ and $$$K_{DKI}$$$ have been estimated by fitting the standard DKI model to the data.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

2845