2842
Comparison of compartmental models of diffusion MRI for assessing myocardial microstructure1Cardiovascular & Metabolic Medicine, University of Leeds, Leeds, United Kingdom, 2Cardiovascular Medicine, University of Oxford, Oxford, United Kingdom
Synopsis
Diffusion tensor imaging (DTI) is a valuable technique for interrogating tissue microstructure, but the estimated parameters remain an indirect characterisation of the underlying tissue architecture. For direct measurement of biophysical parameters, we propose a two-compartment model to quantify cardiomyocyte radius, volume fraction, and dispersion. The intra- and extra-cellular space were modelled using a cylinder with Bingham distributed axes and an oblate tensor. The model reduced root mean squared error by 5% compared to DTI, with volume fraction = 60%, radius = 5.8𝜇m, and dispersion in the sheetlet plane = 9°. These parameters could serve as biomarkers for characterisation of cardiomyopathies.
Introduction
Diffusion weighted Magnetic Resonance Imaging (DW-MRI) is a valuable method to probing complex microstructure of the heart. Diffusion Tensor Imaging (DTI) is the most frequent technique with the principal eigenvectors reflecting the cardiomyocytes orientation and diffusion metrics indicating the underlying tissue integrity. However, direct measurement of physiologically meaningful parameters such as cell size cannot be achieved by DTI. To address this limitation, model-based approaches are incorporated into DW-MRI techniques of the brain 1. However, their application in heart has been very limited so far 2.This study aims to develop and compare a range of biophysical models to quantify cardiomyocyte size, orientation, dispersion, and volume fraction in the preclinical setting. Different acquisition schemes are investigated to identify, which scheme facilitates biophysical parameter estimation best.
Methods
Sample preparation and data acquisition:Mouse hearts were excised and scanned as previously described 3. In brief, images were acquired on a 9.4T MRI system using a fast spin echo sequence with six gradient strengths, five diffusion times (Δ=10-50ms), and ten diffusion-encoding directions. The remaining imaging parameters are as follows: resolution=187.5𝜇m isotropic, field of view=13.5⨉9⨉9mm, diffusion duration 𝛿=2.5ms, and maximum b-value=2500s/mm2.
Biophysical model:
This study included three models previously proposed by Hsu et al.4, Kim et al.2, and McClymont et al.5, and five new two-compartment models. The total DW-MRI signal is modelled as a linear combination of signals attributed to the intracellular ($$$S_{IC}$$$) and extracellular ($$$S_{EC}$$$) space:
$$S = v_{IC} S_{IC} + v_{EC} S_{EC}$$
where $$${v_{IC},v_{EC}}\in[0,1]$$$ are volume fractions and $$$v_{IC}+v_{EC}=1$$$. To model restricted diffusion in cardiomyocytes, four cylinder models were investigated: the standard cylinder 2, elliptical cylinder 5, cylinder with Gamma distributed radii (GDR) 6, and cylinder with Bingham distributed axes (BDA) (Fig. 1).
Cylinder models, except the elliptical cylinder, are isotropic about the primary diffusion axis. To allow anisotropic diffusion along the second and third diffusion eigenvectors, a pancake model was used to represent the extracellular space. For the elliptical cylinder, both an isotropic ball and a pancake were deployed to model the extracellular space.
Analysis:
To estimate biophysical parameters, the L2-norm
$$J = \sum_{m-1}^{M} [\widetilde{S}_m(\delta, \Delta, \mathbf{g}) - S_m(\delta, \Delta, \mathbf{g}, \mathbf{p})]^2$$
is minimised with respect to model parameters $$$\mathbf{p}$$$ where M=300 is the total number of measurements, $$$\widetilde{S}_m$$$ is the $$$m^{th}$$$ measurement, and $$$S_m$$$ is the predicted signal. To enforce constraints on model parameters, the method of substitution is applied 6. The Levenberg–Marquardt algorithm is then applied to solve the unconstrained non-linear optimisation problem. All experiments are conducted using an in-house Matlab toolkit (Matlab2019b, MA, USA). To assess the fitting performance, the root mean squared error (RMSE) was computed. Estimated biophysical parameters were compared against physiological ranges reported in the literature7-8.
Result
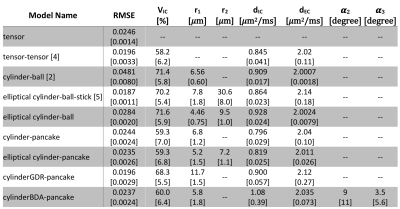
The tensor-tensor model 4 improved the RMSE by ~20% compared to DTI but failed to account for restricted diffusion in cardiomyocytes (Table 1). The cylinder-ball 2 modelled the restricted diffusion and provided reasonable estimates for cardiomyocytes radius but failed to fit data properly; the RMSE was ~95% higher compared to DTI. The model proposed by McClymont et. al. 5 addressed both issues but the estimated radius of 30𝜇m along the secondary diffusion eigenvector was almost twice the physical sizes known from the literature 7.Among the proposed models, the elliptical cylinder-ball had 15% higher RMSE compared to DTI. The remaining four models improved the fitting performance compared to DTI and yielded reasonable estimates of biophysical parameters (Table 1).
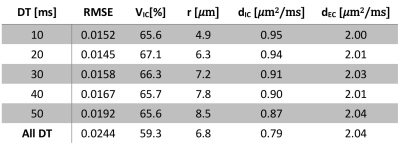
Varying both diffusion times and b-values were found to be essential for accurate parameter estimation. Fixing the b-value similar to 2 underestimated the cell radius and the intracellular volume fraction severely (Table 2). Conversely, fixing the diffusion time similar to 4 biased the estimation of cell radius severely (Table 3).
Discussion
An acceptable biophysical model should not only fit the data sufficiently well, but also provide a plausible sketch of the underlying tissue microstructure. Despite the merits of the previously proposed models, they do not satisfy either of these criteria due to poor fitting performance or unrealistic parameter estimation as confirmed in this work (Table 1). Five new models were studied here, out which four models improved the fitting performance compared to DTI and yielded parameters in agreement with reported physiological ranges. The cylinderBDA-pancake model represents anatomical findings closest as it also allows for modelling dispersion. Given the resolution of ~200𝜇m, the helix angle may vary up to 30° in one voxel. For the cylinderBDA-pancake, the intracellular volume fraction, cardiomyocyte radius, and cell dispersion were estimated as 60%, 5.8𝜇m, and 9°.To facilitate parameter estimation for biophysical models, new bespoke acquisition schemes are required that collect multi-diffusion-time, multi-shell, and multi-direction data. Here we showed that previous acquisitions schemes that only acquired a single shell with different diffusion times or multiple shell but with a single diffusion time are insufficient.
Conclusion
We proposed and compared five new two-compartment models to quantitate microstructure in a healthy mouse heart ex vivo. These models had superior performance than previous models in terms of data fitting and yielded plausible estimates of biophysical parameters. For reliable and robust estimation of biophysical parameters, bespoke acquisition schemes are required. These parameters could serve as valuable quantitative biomarkers for the characterisation of hypertrophy and fibrosis.Acknowledgements
This work was supported by the British Heart Foundation (BHF) [grant numbers PG/17/28/32943, PG/19/1/34076 and RG/13/8/30266].References
1. I. O. Jelescu and M. D. Budde, “Design and validation of diffusion MRI models of white matter.,” Front. Phys., vol. 28, Nov. 2017.
2. S. Kim, G. Chi-Fishman, A. S. Barnett, and C. Pierpaoli, “Dependence on diffusion time of apparent diffusion tensor of ex vivo calf tongue and heart,” Magn. Reson. Med., vol. 54, no. 6, pp. 1387–1396, 2005.
3. I. Teh et al., “Resolving fine cardiac structures in rats with high-resolution diffusion tensor imaging,” Sci. Rep., vol. 6, no. April, p. 30573, 2016.
4. E. W. Hsu, D. L. Buckley, J. D. Bui, S. J. Blackband, and J. R. Forder, “Two-component diffusion tensor MRI of isolated perfused hearts,” Magn. Reson. Med., vol. 45, no. 6, pp. 1039–1045, 2001.
5. D. McClymont, I. Teh, H. Whittington, C. Lygate, and J. Schneider, “Inferring cell morphology in the heart with a compartment model of diffusion MRI,” in In proceedings of the 25th Annual Meeting of ISMRM, Hawaii, 2017.
6. E. Panagiotaki, T. Schneider, B. Siow, M. G. Hall, M. F. Lythgoe, and D. C. Alexander, “Compartment models of the diffusion MR signal in brain white matter: A taxonomy and comparison,” Neuroimage, vol. 59, no. 3, pp. 2241–2254, 2012.
7. Y. F. Chen, S. Said, S. E. Campbell, and A. M. Gerdes, “A method to collect isolated myocytes and whole tissue from the same heart,” Am. J. Physiol. - Hear. Circ. Physiol., vol. 293, no. 3, pp. 2006–2008, 2007.
8. J. Greiner, A. C. Sankarankutty, G. Seemann, T. Seidel, and F. B. Sachse, “Confocal microscopy-based estimation of parameters for computational modeling of electrical conduction in the normal and infarcted heart,” Front. Physiol., vol. 9, no. APR, 2018.
Figures
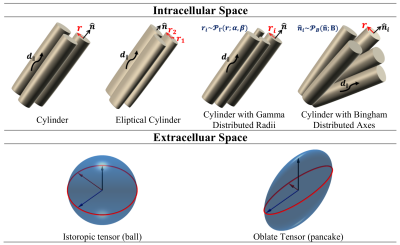
Figure 1. Intracellular and extracellular compartment models.