Introduction

Magnetic resonance (MR) $$$T_2^*$$$ mapping is widely used to study iron deposition, hemorrhage and calcification in the tissue. To reduce the long scan time needed for high-resolution 3D $$$T_2^*$$$ mappings, measurements are undersampled in the $$$k$$$-space, and sparse prior on the wavelet coefficients of images can be used to fill in the missing information via compressive sensing^1,2. Conventional regularization-based reconstruction approaches enforce the sparse prior via regularization functions such as the $$$l_1$$$ norm^3,4. However, they require extensive parameter tuning, and the parameters tuned on the training data often do not work best on the test data. We propose a Bayesian formulation for $$$T_2^*$$$ mapping so that the parameters can be automatically and adaptively estimated for each dataset.

Proposed Method

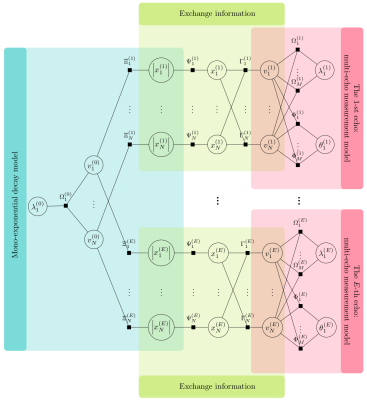
From a Bayesian perspective, the wavelet coefficients $$$\boldsymbol v$$$ of images are assumed to follow a prior distribution $$$p(v|\lambda)$$$ such as Laplace distribution that produces sparse signals: $$$p(v|\lambda) =\lambda\exp(-\lambda|v|)$$$, where $$$\lambda$$$ is the prior distribution parameter. The measurement noise $$$\boldsymbol w$$$ is assumed to be i.i.d. white Gaussian: $$$p(w|\theta)=\mathcal{N}(w;0,\theta)$$$, where $$$\theta$$$ is the noise variance. Given the noisy measurements $$$\boldsymbol y$$$, we can compute the posterior distribution $$$p(v|\boldsymbol y)$$$ via sum-product approximate message passing (AMP)⁵. The minimum-mean-square-error estimation of the signal is then the mean of $$$p(v|\boldsymbol y)$$$, i.e. $$$\hat{v} = \mathbb{E}(v|\boldsymbol y)$$$. We can estimate the distribution parameters by treating them as random variables and maximizing their posteriors⁶, i.e. $$$\hat{\lambda}=\arg\max_{\lambda} p(\lambda|\boldsymbol y)$$$.

AMP was originally developed for linear system. Since the MR signal intensity $$$|x|$$$ follows the nonlinear mono-exponential decay as a function of echo time, the standard AMP could not be used to recover the $$$T_2^*$$$ map. We propose a new nonlinear AMP framework that incorporates the mono-exponential decay model, and use it to recover the $$$T_2^*$$$ map. As shown in Fig. 1, there are mainly three parts in the factor graph of the proposed AMP framework. The mono-exponential decay block encodes the nonlinear relationships among the longitudinal magnetization $$$\boldsymbol x^{(0)}$$$, the $$$T_2^*$$$ map and the MR signal intensities $$$|\boldsymbol x^{(i)}|$$$ at multiple echoes, $$$i=1,\cdots,E$$$. The multi-echo measurement blocks encode the linear relationships between the $$$k$$$-space measurements $$$\boldsymbol y$$$ and the $$$T_2^*$$$-weighted complex images $$$\boldsymbol x^{(i)}$$$ at multiple echoes. The exchange blocks encode the nonlinear relationship between the MR signal intensities $$$|\boldsymbol x^{(i)}|$$$ and the multi-echo complex images $$$\boldsymbol x^{(i)}$$$. Messages about the variables' distributions are passed among the factor nodes in the factor graph until a consensus on how the variables are distribution is reached, and damping operation can be used to stabilize the convergence of the AMP algorithm.

Experimental Results

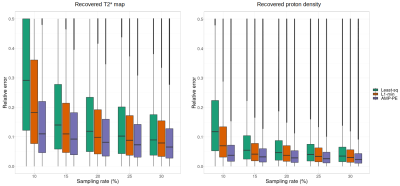
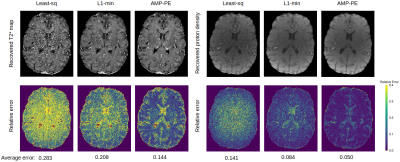
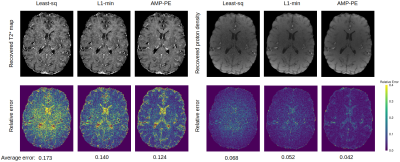
We compared the proposed approach with the baseline least square approach and the state-of-the-art $$$l_1$$$-norm minimization approach on the reconstruction of $$$320\times320$$$ in vivo brain images. The data was acquired on a 3T MRI scanner (Siemens Prisma) with a 32-channel head coil, and the k-space was fully sampled during the acquisition to provide the "gold standard" references for evaluation. The parameters of the acquisition protocol were as follows: the number of echoes=6, the first echo time=7.64ms, echo spacing=5.41ms, slice thickness=0.7mm, resolution=0.6875mm, pixel bandwidth=260Hz, TR=40ms, and FoV=22cm. We uniformly selected $$$20$$$ 2D slices and reconstructed them from undersampled data, where the sampling rates varied between $$$10\%$$$ and $$$30\%$$$. Poisson disk sampling patterns were used to select the sampling locations, and the central $$$24\times 24$$$ k-space was always fully sampled to estimate the coil sensitivity maps. The pixel-wise relative errors in the brain region are computed and shown as box plots in Fig. 2. Taking one 2D slice as an example, Fig. 3 and 4 show the recovered $$$T_2^*$$$ maps and the corresponding relative errors when the sampling rates are $$$10\%$$$ and $$$15\%$$$. Our AMP-PE approach achieves lower relative errors in reconstruction across different sampling rates compared to least-square and $$$l_1$$$-norm minimization approaches.

Discussion and Conclusion

The least square approach does not require parameter tuning since it does not make use of the sparse prior on images during the reconstruction, it thus performed worse than the other two approaches. We tuned the regularization parameter for the $$$l_1$$$-norm minimization approach on training data, which was later used to perform reconstruction on test data. However, the tuned parameter was not necessarily optimal with respect to the test data, which leads to sub-optimal performances as shown in Fig. 2-4. The proposed AMP approach automatically and adaptively estimates the distribution parameters for each dataset, it is more efficient and outperforms the other approaches in all cases, especially when the sampling rate is very low ($$$\approx 10\%$$$). Apart from $$$T_2^*$$$ mapping, the proposed approach can be used to solve other problems arising from MR such as quantitative susceptibility mapping.

Acknowledgements

This work is supported by National Institutes of Health under Grants R21AG064405 and P50AG025688.