2815

Accelerating Quantification of Myelin Water Fraction with Nonlocal Low-Rank Tensor in the Feature Domain

Quan Chen¹, Huajun She¹, and Yiping P. Du¹
¹School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, China

Synopsis

Acceleration of myelin water fraction (MWF) mapping using the Feature domain nonlocal Low-Rank Tensor based (FnLRT) algorithm is investigated in this study. The global temporal information of the whole images is used to project the T2* weighted images (T2*WIs) into the feature domain. The nonlocal and local spatial redundancies in the feature domain are further exploited. The tensor-based decomposition is used to explore the multi-dimensional redundancies. The human brain experiments demonstrate the outperformance of the FnLRT algorithm over the state-of-the-art reconstructions at R=6. The FnLRT algorithm provides the potential to obtain the whole brain MWF mapping in 1 minute.

Introduction

Myelin water quantification provides specific information about the integrity of the myelin sheath in the brain^1,2. The whole brain MWF maps can be obtained by collecting the multi-echo T2*WIs in several minutes^3,4. Acceleration for MWF mapping has been achieved using parallel imaging⁵ and compressed sensing⁶ at a reduction factor (R) of 2. Fast parametric imaging can also be achieved by exploring the low-rank property in the temporary mode^7-9. The high-dimensional low-rank tensor (LRT) reconstruction, which maintains the high-order structure inside the data, has been further used to exploited the temporary redundancy in the multi-contrast datasets^9,10. Whereas, in the spatial mode, the local neighboring pixels have the similar intensity and nonlocal similar patches have homogenous microstructures, the low-rank property existing in the local and nonlocal spatial modes is merely explored. Moreover, the removal of artifacts is usually processed on the noisy multi-contrast images. To improve the recovery from the noisy datasets, a Feature domain nonlocal Low-Rank Tensor based (FnLRT) algorithm is proposed in this study. The proposed FnLRT algorithm has combined the global temporal features of all pixels and the local and nonlocal spatial redundancy in the projected feature domain to jointly improve the quality of the reconstructed T2*WIs.

Theory

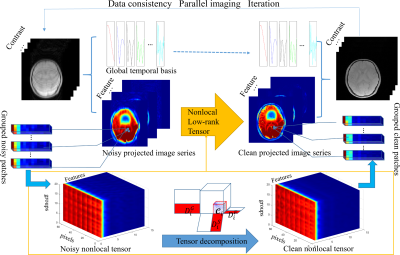
The flowchart of the FnLRT algorithm is illustrated in Figure 1. A temporal orthogonal basis is $$$D^{c}$$$ obtained by the principal component analysis (PCA) feature extraction of all relaxation signals. The full temporal T2*WIs are projected to the feature domain by using the global temporal bases. The nonlocal similarity in the projected image series is explored. The patches are obtained through a sliding operation and represented by the matrices $$$\mathscr{N}_i \in R^{dS \times dF}$$$. $$$dS$$$ and $$$dF$$$ refer to the number of pixels in the spatial domain and the number of contrasts in the temporal domain, respectively. Then, similar patches over the space are grouped together to further extend the matrices into 3-order tensors $$$\mathscr{N}_i \in R^{dS \times dF \times dG}$$$. The expression for FnLRT is $$\underset{x,D,\mathscr{C}}{min}\sum_{i}{\rho \left\|F_usx-y \right\|^2_2+\left\|x\times (D^C)^T-N \right\|^2_2+uf(\mathscr{N}_i)},$$ $$s.t. \left\|\mathscr{N}_i-\mathscr{C}_i \times_1 D_i^S \times_2 D_i^F \times_3 D_i^G \right\|^2_2 < \epsilon, D^TD=I,$$
where $$$x$$$ is the desired images, $$$y$$$ is the undersampled k-space data, $$$s$$$ is the coil sensitivity, and $$$F_u$$$ is the undersampled Fourier operator. $$$\rho$$$ and $$$u$$$ are the regularization parameters, $$$\mathscr{N}_i$$$ refers to the tensor representation of the desired images in the i-th nonlocal patch group. $$$f(\mathscr{N})=R(D)+S(\mathscr{C})$$$ is regularization function used to promote tensor sparsity with sparsity ($$$S$$$) on the core tensor and low-rank constraints ($$$R$$$) on the subspaces. $$$D_i^S$$$, $$$D_i^F$$$, and $$$D_i^G$$$ are the subspaces of the i-th tensor, representing basis functions of the local spatial mode, projected temporal feature mode and nonlocal patch mode, respectively. $$$\mathscr{C}_i$$$ is the core coefficient tensor. $$$\times_n$$$ is the mode-n product of a tensor. $$$\epsilon$$$ is the error threshold parameter.

Methods

Nine healthy subjects were scanned using a multi-slice mGRE sequence on a 3T MRI scanner (uMR790, United Imaging Healthcare, Ltd., Shanghai, China). Written consent was obtained before each scan. The scanning parameters were: FOV = 240×240mm², matrix = 176×176, FA = 90°, TR = 2 s, first TE = 1.95 ms, echo spacing = 1.16 ms, echo train length = 30, slice thickness = 3 mm, 25 slices were scanned with a 1.5 mm slice gap. The whole brain scan time was 5.9 min. A variable-density random phase-encoding mask with R = 6 was used for retrospective undersampling. The proposed algorithm was compared to the state-of-the-art L+S¹¹ and LRT algorithms^9,10. The non-negative jointly sparse (NNJS) algorithm¹² was used for MWF quantification.

Results

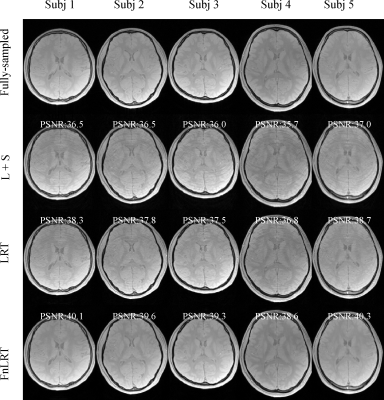
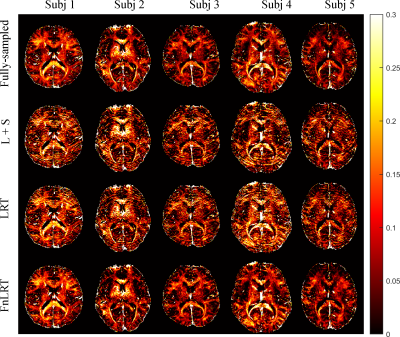
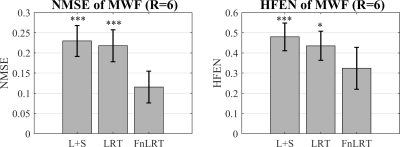
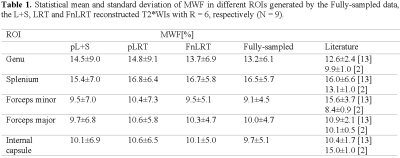
In Figure 2, substantially reduced artifacts are observed in the FnLRT reconstructed T2*WIs compared to the L+S and LRT reconstructed images. The mean PSNRs of the L+S, LRT and FnLRT reconstructions are 36.7, 38.0 and 39.6, respectively. In Figure 3, the MWF maps of FnLRT present high similarity with that of the fully-sampled references, while substantial artifacts remain in the MWF maps of L+S and LRT. The FnLRT algorithm obtains significantly lower NMSE and HFEN than the L+S and LRT algorithms in the statistical comparisons, as demonstrated in Figure 4. In the local regions, the mean MWF values of different ROIs generated from the three reconstructions are consistent with that of the previous studies^2,13, while the MWF maps obtained from the L+S and LRT reconstructions show a higher standard deviation than that of the FnLRT reconstructions, as listed in Table I.

Discussion and Conclusion

The high recovery ability of the proposed FnLRT reconstruction has been demonstrated quantitatively and qualitatively. Reduced artifacts and substantially improved similarity with the fully-sampled references are consistently observed in the FnLRT reconstructed T2*WIs and the corresponding MWF maps compared to the L+S and LRT reconstructed images. The high performance of the FnLRT algorithm may benefit from the projection of the noisy T2*WIs into the feature mode. The artifacts in the feature domain are substantially reduced as shown by the projected image series in Figure 1. The nonlocal grouping will be less affected by the artifacts in the feature domain, then the performance of nonlocal tensor based denosing can be improved. The high-quality MWF maps of the proposed FnLRT reconstruction have validated the feasibility of accelerating MWF quantification at R=6.

Acknowledgements

No acknowledgement found.

References

[1] Mackay AL, Whittall KP, Adler J, Li DKB, Paty DW, Graeb DA. In vivo visualization of myelin water in brain by magnetic resonance. Magn Reson Med 1994;31:673-677.

[2] Whittall KP, MacKay AL, Graeb DA, Nugent RA, Li DK, Paty DW. In vivo measurement of T2 distributions and water contents in normal human brain. Magn Reson Med 1997;37:34-43.

[3] Nam Y, Kim DH, Lee J. Physiological noise compensation in gradient-echo myelin water imaging. Neuroimage 2015;120:345-349.

[4] Lee H, Nam Y, Kim DH. Echo time-range effects on gradient-echo based myelin water fraction mapping at 3T. Magn Reson Med. 2019;81:2799-2807.

[5] Drenthen GS, Backes WH, Aldenkamp AP, Jansen JF, Applicability and reproducibility of 2D multi-slice GRASE myelin water fraction with varying acquisition acceleration. NeuroImage 2019;195:333-339.

[6] Chen H, Majumdar A, Kozlowski P. Compressed sensing CPMG with group-sparse reconstruction for myelin water imaging. Magn Reson Med 2014;71:1166-1171.

[7] Zhao B, Lu W, Hitchens TK, Lam F, Ho C, Liang ZP. Accelerated MR parameter mapping with low-rank and sparsity constraints. Magn Reson Med 2015;74:489-498.

[8] Zibetti MVW, Sharafi A, Otazo R, Regatte RR. Accelerating 3D-T1 mapping of cartilage using compressed sensing with different sparse and low rank models. Magn Reson Med 2018;80:1475-1491.

[9] He J, Liu Q, Christodoulou AG, Ma C, Lam F, Liang ZP. Accelerated high-dimensional MR imaging with sparse sampling using low-rank tensors. IEEE Trans Med Imaging 2016;35:2119-2129.

[10] Christodoulou AG, et al. Magnetic resonance multitasking for motion-resolved quantitative cardiovascular imaging. Nat Biomed Eng 2018;2:215-226.

[11] Otazo R, Candes E, and Sodickson DK. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magn Reson Med 2015;73: 1125-1136.

[12] Chen Q, She H, and Du YP. Improved quantification of myelin water fraction using joint sparsity of T2* distribution. J Magn Reson Imaging 2020;52:146-158.

[13] Zimmermann M, et al. Multi-exponential relaxometry using l1-regularized iterative NNLS (MERLIN) with application to myelin water fraction imaging. IEEE Trans Med Imaging 2019;38: 2676-2686.

Figures

Figure 1. The flowchart of the FnLRT algorithm. The artifacts in the features are substantially reduced.

Figure 2. Comparative results of the first echo T2*WIs reconstructed by the L+S, LRT and FnLRT algorithms at R = 6. The PSNR of the reconstructed T2*WIs of all echoes are showed at the top of the corresponding images.

Figure 3. The MWF maps of 5 representative subjects obtained from the L+S, LRT and FnLRT reconstructions (R = 6).

Figure 4. The statistical NMSE and HEFN of MWF estimated from the L+S, LRT and FnLRT reconstructions with the multi-coil datasets of all subjects at R = 6. Significant differences with P < 0.0001 and P < 0.05 are marked with *** and *, respectively.

Table 1. Statistical mean and standard deviation of MWF in different ROIs generated by the Fully-sampled data, the L+S, LRT and FnLRT reconstructed T2*WIs with R = 6, respectively (N = 9).

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

2815