2720
A general framework for eddy current minimization in Velocity Selective Arterial Spin Labeling
Joseph G. Woods1, Eric C. Wong1, David D. Shin2, and Divya Bolar1
1Department of Radiology, University of California San Diego, San Diego, CA, United States, 2GE Healthcare, Menlo Park, CA, United States
1Department of Radiology, University of California San Diego, San Diego, CA, United States, 2GE Healthcare, Menlo Park, CA, United States
Synopsis
A novel framework that minimizes eddy current mismatch between tag and control acquisitions in velocity-selective (VS) arterial spin labeling is introduced. The framework is based on minimizing the 0th-order gradient moment in the presence of eddy currents and is applicable to any VS module design, without suffering a time penalty in module duration. Simulation and empirical data are presented and demonstrate reductions in eddy current artifacts in both phantom and in vivo data.
Introduction
Velocity selective arterial spin labeling (VSASL) labels arterial blood water by saturation (1,2) or inversion (VSI) (3) using a series of bipolar flow-weighting gradients. Since there should be no flow-weighting in the control image, gradients are either switched off or made monopolar. This results in unbalanced eddy currents (ECs) that manifest as artifactually labeled static tissue signal in the ASL difference images (ΔMz).Several techniques have been suggested to reduce this EC mismatch: 1) reduce VS gradient amplitudes (4), 2) insert padding time after the VS gradients (2,4) and 3) a symmetrically designed 8-segment B1-Insensitive Rotation (BIR-8) VS module (2) for VS saturation. However, options 1 and 2 increase the duration of the VS module, therefore reducing labeling efficiency. Option 3 greatly reduces ECs in VS saturation, but cannot be used for VSI or when a spatially-selective VS module is required, as in Turbo-VSASL (5).
We introduce a framework to minimize EC mismatch between tag and control VS modules for any given VS module design without increasing module duration. This framework optimizes VS gradient timings to minimize the 0th-order gradient moment (m0) in the presence of ECs. We demonstrate this framework with two standard VS modules: double-refocused Hyperbolic Secant (DRHS) and symmetric BIR-8.
Methods
EC induced magnetic fields during the VS module result in a non-zero m0 for the tag condition (and control condition in VSI) resulting in unwanted labeling of static tissue. This effect is demonstrated via Bloch simulation in Figure 1. If EC amplitudes and time-constants are known a priori, the VS gradients can be optimised to minimize m0, while maintaining the desired m1 and VSASL velocity cutoff (Vcut).The proposed framework has the following steps:
- Generate EC time courses as a function of spatial position given empirically measured eddy current amplitudes and time-constants.
- Choose initial VS gradient timings for chosen Vcut.
- Convolve the VS gradient waveforms with the EC time-courses to form the effective gradient fields.
- Calculate the difference in Mz between tag and control modules (ΔMz) for a given set of spatial positions using 3D Bloch simulations and the effective gradient fields.
- Calculate the root-mean-squared (RMS) ΔMz across spatial positions.
- Update the VS gradient timings in optimisation routine while maintaining m1.
- Go to step 3 and repeat; stop if the reduction in RMS ΔMz is below tolerance.
We limited the optimisation to only consider VS gradient durations and positions, which are highlighted in Figure 2.
We measured up to 3rd order EC polynomials on our 3T system (MR750, GE Healthcare, Waukesha, WI) using the higher order EC calibration scan described in (6), with modifications to measure short time constant terms. Measured ECs were used to optimise the VS module timings for each gradient axis. Gradient amplitudes and ramps were fixed at 30mT/m and 0.376ms, with gradient padding times initialized to 0.1ms.
VSASL data were acquired on a silicon-oil phantom and human volunteer to demonstrate the effectiveness of the optimization. For the phantom, a single VS module was applied 10 ms before image readout as described previously (2). In vivo, the VSASL tag/control module was applied 1.5s before image readout (a typical VSASL inflow time, TI), with an unoptimized BIR-8 vascular suppression module placed immediately before the acquisition. Other parameters: TR 4s, TE 15.8ms, 2D-SE spiral readout, 5 slices, resolution 3.1x3.1x8mm3, 20 averages, global background suppression.
Results
Figure 3 shows phantom error maps, calculated from the averaged difference images and normalised by the mean control image. Human perfusion-weighted images are shown in Figure 4, demonstrating the spatial impact of the EC errors relative to the perfusion signal and their reduction when using the proposed framework.Discussion
We present a novel framework for eddy current minimization in VSASL. This framework minimizes 0th-order gradient moments that result in unwanted labeling of static spins that contaminate the ASL signal. The method requires a priori knowledge of EC properties for a given MR system, which needs to be measured only once. Phantom and human data show significant improvement in DHRS VSASL performance after optimization. Subtle improvement is seen for optimized BIR-8 gradients in x and z directions, though slightly worse performance is appreciated in y. We suspect this is related to imperfect EC parameter estimates which slightly reduces optimization fidelity; because the BIR-8 is intrinsically insensitive to EC effects (as seen in Figure 1), this may result in slightly worse y-gradient performance. More robust EC estimation is expected to further reduce BIR-8 EC errors.Dramatic improvements are expected when the framework is applied to i) VSI modules, which are exquisitely sensitive to ECs (3,6), but potentially have the highest SNR of known VS labeling schemes, and ii) slice-selective VS modules, as in Turbo-VSASL, to permit robust, high temporal resolution CBF-FMRI to measure oscillatory neural activity (7).
Conclusion
A general framework for eddy current minimization specific for VSASL is introduced and shown to be effective in reducing eddy-current related artifacts in both phantom and in vivo human data.Acknowledgements
Divya S. Bolar is supported by an RSNA Resident/Fellow Grant.References
- Wong EC, Cronin M, Wu W-C, Inglis B, Frank LR, Liu TT. Velocity-selective arterial spin labeling. Magn. Reson. Med. 2006;55:1334–1341 doi: 10.1002/mrm.20906.
- Guo J, Meakin J a., Jezzard P, Wong EC. An optimized design to reduce eddy current sensitivity in velocity-selective arterial spin labeling using symmetric BIR-8 pulses. Magn. Reson. Med. 2015;73:1085–1094 doi: 10.1002/mrm.25227.
- Qin Q, van Zijl PCM. Velocity-selective-inversion prepared arterial spin labeling. Magn. Reson. Med. 2016;76:1136–1148 doi: 10.1002/mrm.26010.
- Meakin JA, Jezzard P. An optimized velocity selective arterial spin labeling module with reduced eddy current sensitivity for improved perfusion quantification. Magn. Reson. Med. 2013;69:832–838 doi: 10.1002/mrm.24302.
- Bolar DS, Polimeni J, Ohringer N, Adalsteinsson E, Rosen BR. Turbo VSASL: slice- and velocity-selective ASL for high temporal resolution functional CBF mapping. In: Proceedings of the 26th Annual Meeting of the ISMRM, Paris, France. ; 2018. p. 710.
- Xu D, Maier JK, King KF, Collick BD, Wu G, Peters RD, Hinks RS. Prospective and retrospective high order eddy current mitigation for diffusion weighted echo planar imaging. Magn Reson Med. 2013 Nov;70(5):1293-305. doi: 10.1002/mrm.24589. Epub 2013 Jan 16.
- Guo J, Das S, Hernandez‐Garcia L. Comparison of velocity‐selective arterial spin labeling schemes. Magn Reson Med. 2020; 00: 1– 13. Online ahead of print. https://doi.org/10.1002/mrm.28572
- Lewis LD, Setsompop K, Rosen BR, Polimeni JR. Fast fMRI can detect oscillatory neural activity. PNAS. 2016;113(43): E6679-E6685 doi:10.1073/pnas.1608117113
Figures
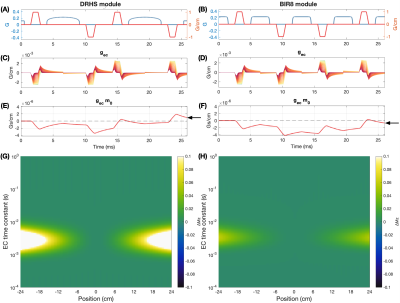
Pulse sequences for nonselective DRHS (A) and BIR8 (B) VS modules. (C) and (D) show induced EC gradient amplitudes for each module for 100 time-constants logarithmically spaced between 0.1 ms and 1 s (red to yellow), with amplitude of -0.25%. (E) and (F) show m0 over time for the time-constant with the largest final m0 for each module. Substantial non-zero final m0 for the eddy current gradients (black arrows) are seen . (G) and (H) show the fractional control-tag static tissue error in the longitudinal magnetization, Mz, across time-constants and position.
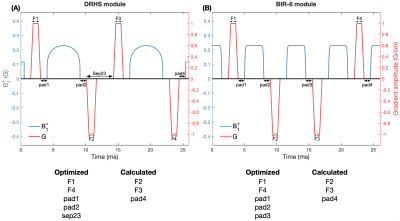
Schematics of the DRHS and BIR-8 VS modules. The optimization was restricted to only consider the gradient durations and positions. Five timing parameters in each module were optimized, with the remaining timings being calculated to achieve the desired Vcut. To constrain the overall VS module duration, pad1 + pad4 had to equal twice the initialised value (0.1 ms).
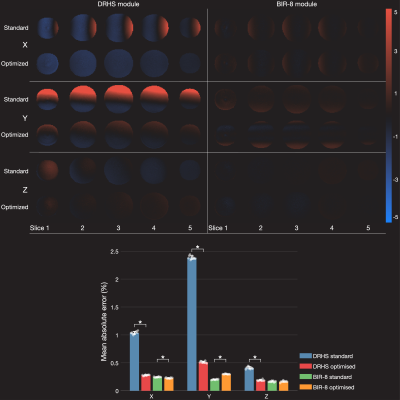
Phantom error maps (% error) reflecting residual eddy current effects before and after VS gradient optimization, for DHRS and BIR8 VS labeling schemes. The bar graph reflects the mean absolute error across the phantom volume. Significant improvements are seen for the x, y, and z gradient axes for DHRS. The BIR-8 errors are small for each gradient axis, and little or no improvement was seen.
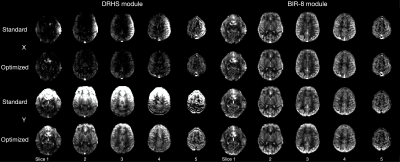
Human perfusion-weighted images acquired before and after VS gradient optimization for both DHRS and BIR-8 VS modules in x and y gradient directions. z direction was not acquired due to subject intolerance. Marked EC effects are seen for the standard DHRS approach, which are qualitatively improved after optimization. BIR-8 errors are small for each gradient axis, and little or no improvement was seen.