Introduction

As a tool for quantitative perfusion measurement, MRF-based (Magnetic Resonance Fingerprinting) Arterial Spin Labeling (ASL) is gaining increasing popularity [1],[2],[3],[4] due to its ability to simultaneously yield unbiased estimates of perfusion and multiple other hemodynamic parameters and tissue properties. However, to realize its potential for use in clinical imaging, MRF-ASL needs to be able to provide unbiased estimates of perfusion for an extensive region of the brain in a relatively short period of time. This presents a challenge because shorter labeling durations inevitably result in fingerprints that contain less information about perfusion. Velocity Selective Inversion (VSI) pulses [5] have garnered attention for being particularly sensitive to perfusion, while being able to eliminate nuisance parameters like magnetization transfer from the signal model, and producing signals having reduced sensitivity to bolus arrival time (BAT) effects[6]. In this work, we aim to use VSI pulses in conjunction with an MRF-ASL framework to quantify perfusion across multiple slices of the brain. Furthermore, with the aid of Velocity Selective Saturation (VSS) pulses across all acquired images in the fingerprint, we also eliminate sensitivity of the ASL fingerprints to the Cerebral Blood Volume (CBV) fraction.

Methods

In our work, the ASL preparation was done with a VSI pulse—either velocity selective (label) or non-selective (control), a variable post-labeling delay, and a VSS pulse for arterial suppression before acquisition. Fig. 1 shows a single repetition period for this method. The generated VSI pulses were based upon the method described in [7].

The theorized model for our work effectively has two compartments: tissue and artery. The arterial compartment is further separated into two components, $$$M_{\text{art}}$$$ and $$$M_{\text{art-ex}}$$$, to represent fast and slow-moving spins, respectively. While there is a continuum of spin velocities in an artery, we use these compartments to segregate the spins that are fast enough to not be inverted by the selective inversion pulses from the spins that move slowly enough (especially when exchanging with tissue) to be inverted. We describe the signal in the tissue compartment as:
$$\frac{dM_{\text{tis}}(t)}{dt} = -\frac{M_{\text{tis}}^0-M_{\text{tis}}(t)}{T_{1,\text{tis}}}+f\cdot M_{\text{art-ex}}(t) - \frac{f}{\lambda}\cdot M_{\text{tis}}(t),$$
where $$$M_{\text{art-ex}}$$$ is an arterial exchange compartment that represents the blood in the artery at the exchange site, consisting of slow-moving spins, $$$f,\lambda,M_{\text{tis}}$$$ represent the perfusion, blood-brain partition coefficient and magnetization in the tissue compartment, respectively. To incorporate the effects of VSI pulses on the fast-moving spins in arterial blood, a separate compartment is included which represents the arterial blood $$$M_{\text{art}}$$$. Spins enter the arterial compartment at a ‘fast’ velocity, and slow down before exchanging into the tissue compartment after a delay. We track this behavior by modeling the fast and slow/exchanging spins separately:
$$\frac{dM_{\text{art}}(t)}{dt}=-\frac{M_{\text{art}}^0-M_{\text{art}}}{T_{1,\text{art}}}\\\frac{dM_{\text{art-ex}}(t)}{dt}=-\frac{M_{\text{art-ex}}^0-M_{\text{art-ex}}(t)}{T_{1,\text{art}}}.$$
However, at the end of every BAT, the contents of the $$$M_{\text{art}}$$$ sub-compartment transfer over to the $$$M_{\text{art-ex}}$$$ sub-compartment as follows:
$$M_{\text{art}}(t^*+\text{BAT})=M_{\text{art-ex}}(t^*+\text{BAT}),$$
where $$$t^*$$$ denotes the time at which a velocity selective pulse is applied.
To model the effects of the various velocity selective pulses we introduce three labeling efficiencies into our model, namely $$$\alpha_{\text{ti}},\alpha_{\text{ai}}~$$$and$$$~\alpha_{\text{ts}}$$$.$$$\alpha_{\text{ti}},\alpha_{\text{ai}}$$$ dictate the extent to which the VSI pulses invert spins in tissue and artery respectively, while $$$\alpha_{\text{ts}}$$$ dictates the extent of inversion in slow-moving tissue spins due to a velocity selective saturation pulse. We express these effects mathematically as:

• Velocity Selective Inversion (label)

$$M_{\text{art}}(t+\Delta t)=\alpha_{\text{ai}}\cdot M_{\text{art}}(t)\\M_{\text{tis}}(t+\Delta t)=(1-2\alpha_{\text{ti}})\cdot M_{\text{tis}}(t)$$

• Velocity Selective Non-inversion (control)

$$M_{\text{art}}(t+\Delta t)=(1-2\alpha_{\text{ai}})\cdot M_{\text{art}}(t)\\M_{\text{tis}}(t+\Delta t)=(1-2\alpha_{\text{ti}})\cdot M_{\text{art}}(t)$$

• Velcity Selective Saturation

$$M_{\text{art}}(t+\Delta t)=0\\M_{\text{tis}}(t+\Delta t)=(1-2\alpha_{\text{ts}})\cdot M_{\text{tis}}(t)$$
Typical values for $$$\alpha_{\text{ti}},\alpha_{\text{ai}}~$$$and$$$~\alpha_{\text{ts}}$$$ are obtained from separate Bloch simulations of the VSI pulses. Finally, the observed signal is given by:
$$s(t)=\big(\mathrm{CBV_a}\cdot M_{\text{art}}+(1-\mathrm{CBV_a})\cdot M_{\text{tis}}\big)\cdot\sin{\beta},$$ where $$$\beta$$$ is the flip angle.
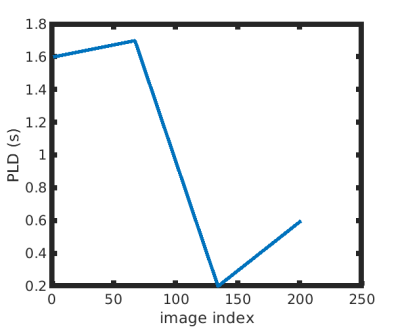
We test our method by estimating perfusion, BAT and tissue $$$T_1$$$ on two healthy subjects. The PLDs in our fingerprint were varied according to the schedule in Fig. 2. The total duration for the scan was $$$600$$$s for $$$18$$$ slices across the brain. The data was acquired on a 3T GE MR750 scanner using a 32-channel Nova Medical coil. The matrix size was $$$64\times 64\times 18$$$, resolution=$$$3.5\times 3.5\times 6$$$mm³ ,TE = $$$15$$$ms, bandwidth=$$$125$$$kHz, fast spin echo stack of spirals readout.

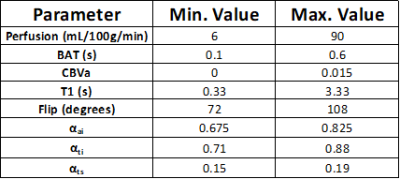
For estimation, we used individual neural networks for each parameter with two hidden layers and $$$100$$$ nodes in each layer. The networks were trained with $$$6\times 10^6$$$ synthetic fingerprints generated from a Bloch simulation of the model described above. The ground truth parameters for the training data were varied uniformly across the range shown in Fig 3. White Gaussian noise with standard deviation of $$$0.003$$$ was added to the fingerprints during training. The ADAM algorithm [8] was used as an optimizer.

Results

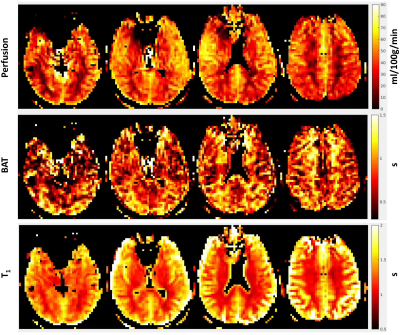
Fig 4 shows the results for quantifying perfusion, BAT and $$$T_1$$$ using our proposed VSIASL+MRF technique for one human subject (4 of 18 slices). The predicted perfusion values in gray and white matter are consistent with those found in ASL literature, and the contrast between gray and white matter values is also as expected. This observation was consistent across both subjects.

Conclusion

We conclude that estimation of perfusion using an MRF-ASL framework combined with VSI pulses is feasible and allows for the estimation of multiple hemodynamic parameters in the brain without hindrance from nuisance parameters, though further validation against other methods is required both in-vivo and in-silico.