Introduction

Optimal sampling strategy has been used in pseudo-continuous arterial spin labelling (pCASL) to obtain protocols designed to achieve higher CBF estimation accuracy¹. Previous work has shown that while these protocols may perform better under an ideal kinetic model, they could be sensitive to macrovascular contamination (MVC), leading to high CBF estimation error². This simulation work systematically investigates the CBF estimation sensitivity to MVC in a comprehensive set of optimal pCASL protocols³, and demonstrates that adding a macrovascular compartment in the estimation model could benefit CBF estimation in most of the scenarios.

Methods

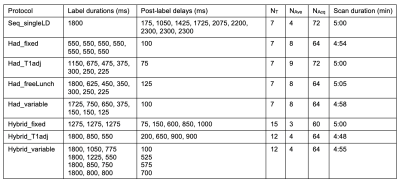
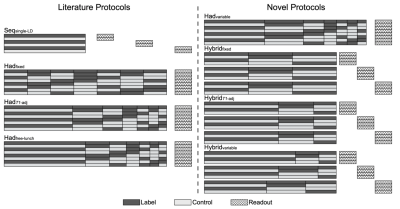
We selected eight representative optimal pCASL protocols³ including a sequential multi-PLD protocol (Seq_singleLD), four time-encoded multi-LD protocols with various label duration block types (Had_fixed, Had_T1adj, Had_freeLunch, Had_variable), and three time-encoded multi-PLD (‘Hybrid’) protocols (Hybrid_fixed, Hybrid_T1adj, Hybrid_variable). The protocol timings and schematics are shown in Table 1 and Figure 1, respectively. PCASL signals using the general kinetic model⁴ (GKM) with a macrovascular component⁵ were simulated and added Gaussian white noise⁶ to give an SNR of 10. The arterial blood volume (aBV) of the macrovascular component varied between 0 and 2.0%. Tissue ATT (ATT_t) ranged from 0.5s to 3.0s, with the macrovascular transit time (ATT_a) varied between 0 to each ATT_t. Other simulation parameters can be found in Table 2. The signals were then fitted with two models in the BASIL toolkit of FSL⁷: GKM and GKMmvc, the latter explicitly accounting for the macrovascular signal. CBF and ATT estimation errors were obtained and averaged over 500 simulations. To quantify CBF sensitivity to MVC we calculated the slopes of the line of best fit of the CBF estimation error curves (unit: error% per 1% aBV) at each combination of ATT_t and ATT_a. Sensitivity values across the simulated ATT_t and ATT_a ranges were used to generate a CBF sensitivity map for each individual protocol.

Results and Discussion

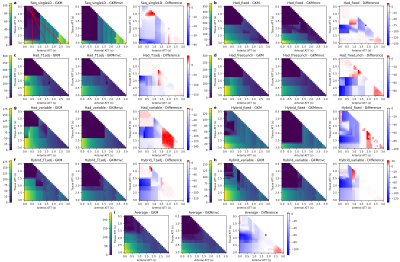
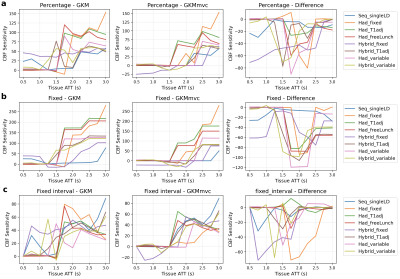
Figure 2a to 2h shows the CBF sensitivity maps for each protocol under the model GKM and GKMmvc and their difference maps (GKMmvc - GKM). The mean CBF sensitivity map is shown in Figure 2i as a measure of the average CBF estimation sensitivity to MVC in all tested protocols. Common features among all protocols could be observed: The general kinetic model had relatively low CBF sensitivity when tissue ATT was shorter than 1.5s (top left of the map). The extended model GKMmvc can reduce the CBF sensitivity to MVC under most conditions, indicated by the negative values on the difference maps. In particular, GKMmvc had the most reduction effect at 1.8s < ATT_t < 2.3s. Under each protocol, both models had the global maximum CBF sensitivity at ATT_t = 3.0s and ATT_a = 0.0s (bottom left of the map). This is when the tissue signal and the macrovascular signal have the largest gap, and therefore macrovascular signal has the highest possibility of being recognised as tissue perfusion by the models, even being explicitly accounted for in GKMmvc. When both ATT_t and ATT_a were prolonged (bottom right of the map), GKMmvc did not have an apparent advantage over GKM.

To compare the CBF sensitivity across protocols, three assumptions of the relationship of ATT_t and ATT_a were considered: percentage (ATT_a = δ × ATT_t), fixed (ATT_a = δ[s]), and fixed interval (ATT_a = ATT_t - δ[s]). For simplicity we took δ = 0.5 in each scenario, which corresponds to the three red lines in Figure 2a. Figure 3 shows the CBF sensitivity for all protocols under each assumption as a function of tissue ATT. There were not consistent patterns across protocols using GKM. When fitted with GKMmvc, Hadamard-encoded protocols were nearly insensitive to MVC in the range of ATT_t < 1.5s, whereas hybrid protocols may have negative CBF sensitivity values. In ‘percentage’ and ‘fixed’ types, hybrid protocols generally had lower CBF sensitivity than Hadamard-encoded protocols when ATT_t > 2.0s, which is beyond the optimised ATT_t range of all protocols. This is consistent with the results in the previous study³ which found Hybrid_T1adj to be the most accurate and robust CBF estimation protocol.

Conclusions

We have demonstrated that while time-encoded and multi-PLD pCASL protocols can be optimised for CBF accuracy, the use of the general kinetic model can still lead to high sensitivity to macrovascular contamination. By adding a macrovascular compartment in the model, the sensitivity to MVC was alleviated, particularly when 1.8s < ATT_t < 2.3s. This indicates the extra step in modelling is beneficial to CBF estimation in the normal ATT_t range. However, the extended model could not account for MVC when prolonged tissue ATT was present, specifically beyond the range for which these protocols had been optimised, especially when macrovascular ATT was short. We propose that the sensitivity map introduced here could be used to examine a protocol for possible MVC effects prior to scanning, or when interpreting results after data collection.

Acknowledgements

This work received funding from the Engineering and Physical Sciences Research Council (EP/P012361/1). The Wellcome Centre for Integrative Neuroimaging is supported by core funding from the Wellcome Trust (203139/Z/16/Z).