2687
Open Source Random Matrix Theory Software for the Analysis of Functional Magnetic-Resonance Imaging Examinations
Derek Berger1, Gurpreet S Matharoo1,2,3, and Jacob Levman1
1Computer Science, St. Francis Xavier University, Antigonish, NS, Canada, 2Physics, St. Francis Xavier University, Clydesdale, NS, Canada, 3ACENET, St. Francis Xavier University, Antigonish, NS, Canada
1Computer Science, St. Francis Xavier University, Antigonish, NS, Canada, 2Physics, St. Francis Xavier University, Clydesdale, NS, Canada, 3ACENET, St. Francis Xavier University, Antigonish, NS, Canada
Synopsis
We assess the potential application of RMT-based features for the analysis of functional MRI (fMRI) across diverse datasets. As novel contributions, we (1) assess the potential for RMT-inspired, whole-brain features extracted from voxel-wise functional connectivity, (2) assess these features’ predictive—rather than explanatory—value, (3) investigate the effect of varying RMT analysis methods on the robustness of study findings, and (4) make general-purpose code publicly available for users to extract these features from a wide variety of data. We find preliminary evidence suggesting that RMT-inspired features may have unique potential in analyses of fMRI functional connectivity.
Introduction
Previous studies have investigated the potential of using analytic techniques from Random Matrix Theory (RMT) to investigate magnetic resonance imaging (MRI) data. In functional magnetic resonance imaging (fMRI), changes in the blood-oxygenation-level-dependent (BOLD) signals are related to neural activity. It is common to investigate statistical relationships between the BOLD signals through functional connectivity analyses, where correlations between collections of these signals are examined to infer connections between different voxels or regions-of-interest (ROIs) within the brain.Whether in the presence of experimental stimuli, or the relative absence, as in a resting state, complex functional connectivity networks are ubiquitous [1]–[4]. This complexity suggests fMRI is a candidate to be studied using Random Matrix Theory (RMT), a set of mathematical tools originally developed some 50 years ago to solve complex problems in nuclear physics [5], [6]. RMT analyses distil a large collection of time varying signal source data into a series of statistical metrics that characterize deviations from expectation, had the signal sources been of a purely random nature. Thus, in the case of fMRI, an RMT analysis will process an entire examination and provide a series of statistics that could be relied upon (individually or combined) for characterizing functional activity in the subject’s brain.
RMT has been used to evaluate the quality of whole brain features extracted from fMRI data [7-8]. RMT has also been used in ROI-based fMRI functional-connectivity studies to investigate differences between rest and task states [9], between subjects with and without attention deficit hyperactivity disorder (ADHD) [10], and between pain and non-pain states [11]. Across these three studies, the spectra of resting or low-attention states exhibited properties close to expectation based on the Gaussian Orthogonal Ensemble. This implies potential for the use of RMT for characterizing high-attention and non-rest states from fMRI examinations.
In this study, we use a novel, voxel-based approach, and expand the applications of RMT to analyse fMRI examinations from diverse datasets. We extract RMT-inspired whole-brain features from voxelwise functional connectivity data, and assess the predictive value of these features. We also present open source software to assist any lab in conducting their own RMT based analyses [12].
Methods
We assess the potential application of RMT-based features for the analysis of functional MRI (fMRI) across diverse datasets. As novel contributions, we (1) assess the potential for RMT-inspired, whole-brain features extracted from voxel-wise functional connectivity to contain information useful for classifying between various psychological processes, (2) assess these features’ predictive—rather than explanatory—value, (3) investigate the effect of varying RMT analysis methods on the robustness of study findings, and (4) make general-purpose code publicly available for users to extract these features from a wide variety of (matrix) data. Open source software [12] was created in python.Table 1 provides a listing of the public domain fMRI datasets used in this analysis. Table 2 provides a listing of all of the RMT derived statistics produced by our open source software [12] and included in this analysis.
Results
We find preliminary evidence suggesting that RMT-inspired features may have unique potential in analyses of fMRI functional connectivity. Space constraints preclude presentation of most of the results of these experiments, however, we present the findings producing the largest group-wise differences between subjects in the datasets analysed. Specifically, Figure 1 provides the results of the RMT based spectral rigidity, which is itself a one-dimensional vector for each subject. Results demonstrate major group-wise differences between patients taking duloxetine (a medication for neuropathic pain) and patients in a non-pain state. Figure 2 provides the results of the RMT based level number variance, which also demonstrates major group-wise differences between patients taking neuropathic pain medication and patients in a non-pain state.Discussion
RMT presents a novel approach to fMRI data analysis, producing an array of statistics that can help characterize deviations from random expectation, thus can potentially help characterize structure in the patterns of data acquired during an examination. Theoretically, RMT statistics may help characterize a variety of medical conditions, may contribute to improving the performance of machine learning algorithms, and may form a component of the next generation of diagnostic tests tasked with assisting in improving the standard of patient care. Results prior to this analysis [11], previously indicated considerable potential from the application of RMT for characterizing pain states. Our analysis furthers that finding with a demonstration of major group-wise differences between patients taking neuropathic pain medication and those not experiencing pain. Thus, early findings imply that RMT may have utility in the characterization of brain function, including the brain’s response to the experience of pain.Acknowledgements
This work was supported by a Natural Science and Engineering Research Council of Canada's Canada Research Chair grant (grant number 231266) to JL, a Canada Foundation for Innovation and Nova Scotia Research and Innovation Trust infrastructure grant (R0176004) to JL, a Natural Science and Engineering Research Council of Canada Discovery Grant (R0192004) to JL and a St. Francis Xavier University research startup grant to JL (grant number R0168020).References
[1] R. L. Buckner, J. R. Andrews-Hanna, and D. L. Schacter, “The Brain’s Default Network: Anatomy, Function, and Relevance to Disease,” Annals of the New York Academy of Sciences, vol. 1124, no. 1, pp. 1–38, Mar. 2008, doi: 10.1196/annals.1440.011. [2] M. D. Fox, A. Z. Snyder, J. L. Vincent, M. Corbetta, D. C. Van Essen, and M. E. Raichle, “From The Cover: The human brain is intrinsically organized into dynamic, anticorrelated functional networks,” Proceedings of the National Academy of Sciences, vol. 102, no. 27, pp. 9673–9678, Jul. 2005, doi: 10.1073/pnas.0504136102. [3] J. Gonzalez-Castillo and P. A. Bandettini, “Task-based dynamic functional connectivity: Recent findings and open questions,” NeuroImage, vol. 180, pp. 526–533, Oct. 2018, doi: 10.1016/j.neuroimage.2017.08.006. [4] A. M. Hermundstad et al., “Structural foundations of resting-state and task-based functional connectivity in the human brain,” Proceedings of the National Academy of Sciences, vol. 110, no. 15, pp. 6169–6174, Apr. 2013, doi: 10.1073/pnas.1219562110. [5] T. Guhr, A. Müller–Groeling, and H. A. Weidenmüller, “Random-matrix theories in quantum physics: common concepts,” Physics Reports, vol. 299, no. 4–6, pp. 189–425, Jun. 1998, doi: 10.1016/S0370-1573(97)00088-4. [6] M. L. Mehta, Random matrices, 3rd ed. Amsterdam ; San Diego, CA: Academic Press, 2004. [7] M. Voultsidou, S. Dodel, and J. M. Herrmann, “Feature evaluation in fMRI data using random matrix theory,” Comput. Visual Sci., vol. 10, no. 2, pp. 99–105, Jun. 2007, doi: 10.1007/s00791-006-0037-6. [8] A. A. Vergani, S. Martinelli, and E. Binaghi, “Resting state fMRI analysis using unsupervised learning algorithms,” Computer Methods in Biomechanics and Biomedical Engineering: Imaging & Visualization, vol. 0, no. 0, pp. 1–14, Jul. 2019, doi: 10.1080/21681163.2019.1636413. [9] R. Wang, Z.-Z. Zhang, J. Ma, Y. Yang, P. Lin, and Y. Wu, “Spectral properties of the temporal evolution of brain network structure,” Chaos, vol. 25, no. 12, p. 123112, Dec. 2015, doi: 10.1063/1.4937451. [10] R. Wang, L. Wang, Y. Yang, J. Li, Y. Wu, and P. Lin, “Random matrix theory for analyzing the brain functional network in attention deficit hyperactivity disorder,” Phys. Rev. E, vol. 94, no. 5, p. 052411, Nov. 2016, doi: 10.1103/PhysRevE.94.052411. [11] G. S. Matharoo and J. A. Hashmi, “Spontaneous back-pain alters randomness in functional connections in large scale brain networks: A random matrix perspective,” Physica A: Statistical Mechanics and its Applications, vol. 541, p. 123321, Mar. 2020, doi: 10.1016/j.physa.2019.123321. [12] D. Berger, stfxecutables/empyricalRMT: Preliminary Release. Zenodo, 2020 (https://pypi.org/project/empyricalRMT/). [13] K. J. Gorgolewski et al., “A high resolution 7-Tesla resting-state fMRI test-retest dataset with cognitive and physiological measures,” Sci Data, vol. 2, no. 1, p. 140054, Dec. 2015, doi: 10.1038/sdata.2014.54. [14] P. Tétreault, A. Mansour, E. Vachon-Presseau, T. J. Schnitzer, A. V. Apkarian, and M. N. Baliki, “Brain Connectivity Predicts Placebo Response across Chronic Pain Clinical Trials,” PLOS Biology, vol. 14, no. 10, p. e1002570, Oct. 2016, doi: 10.1371/journal.pbio.1002570. [15] E. DuPre, W.-M. Luh, and R. N. Spreng, “Multi-echo fMRI replication sample of autobiographical memory, prospection and theory of mind reasoning tasks,” Sci Data, vol. 3, Dec. 2016, doi: 10.1038/sdata.2016.116. [16] T. M. Madhyastha, M. K. Askren, P. Boord, and T. J. Grabowski, “Dynamic Connectivity at Rest Predicts Attention Task Performance,” Brain Connectivity, vol. 5, no. 1, pp. 45–59, Feb. 2015, doi: 10.1089/brain.2014.0248. [17] A. C. Schapiro, E. A. McDevitt, T. T. Rogers, S. C. Mednick, and K. A. Norman, “Human hippocampal replay during rest prioritizes weakly learned information and predicts memory performance,” Nat Commun, vol. 9, Sep. 2018, doi: 10.1038/s41467-018-06213-1.Figures
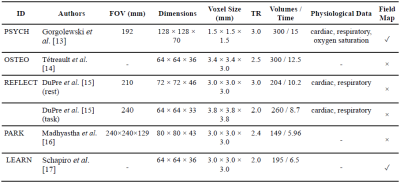
Table 1. Summary of scan parameters. ID = Identifier for this
paper. FOV = Field of View. TR = Time of Repetition (seconds). Time = total
duration (minutes) of each scan. Dimensions listed as M × N × P, indicate P
slices with dimensions M × N.

Table 2. Final RMT features evaluated across all
datasets and computed by our public domain software package [12].
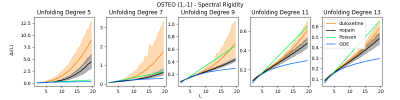
Figure 1. Spectral rigidity for controls (nopain) vs. those with
osteopathic pain taking duloxetine. Solid lines indicate group mean rigidity,
and shaded regions correspond to 99% percentile bootstrapped intervals for each
group. Vertical axes vary to better depict overlap.
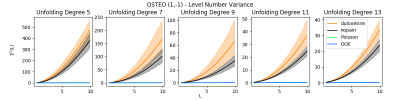
Figure 2. Level variance
for controls (nopain) vs. those with osteopathic pain taking duloxetine. Solid
lines indicate group mean rigidity, and shaded regions correspond to 99%
percentile bootstrapped intervals for each group. Vertical axes vary to better depict overlap.