2685

Low-rank and sparse simultaneous blind estimation of global fluctuations and neuronal-related activity from fMRI data.

Eneko Uruñuela¹, Stefano Moia¹, and César Caballero-Gaudes¹
¹Basque Center on Cognition, Brain and Language, Donostia - San Sebastián, Spain

Synopsis

We propose a novel deconvolution approach to overcome the detrimental effect of global signal fluctuations on the estimates of neuronal-related activity from fMRI data to blindly map single-trial BOLD events without prior information of their timings. We demonstrate that the low-rank and multivariate SPFM algorithm can estimate global signals related to motion in our task, while estimating neuronal-related activity with high fidelity, and benchmark it against sparsity-promoting deconvolution approaches and conventional GLM analysis. This method allows exploring the brain’s functional dynamics during task, naturalistic and resting state paradigms, being less affected by motion and physiologically related fluctuations.

Introduction

Global signal changes due to head jerks, hardware artifacts, or prominent non-neuronal physiological events (e.g. deep breaths)^1,2 can considerably diminish the performance of deconvolution algorithms of fMRI data that aim to blindly reveal the underlying neuronal-related signal related to BOLD events. These algorithms are useful in resting-state, naturalistic paradigms or clinical studies, where the timing of the neuronal activity is unknown, inaccurate, or insufficient^3-7. Such global fluctuations are difficult to compensate for during data preprocessing⁸ and can be misinterpreted as neuronally related since their temporal signature can resemble the hemodynamic response function (HRF) assumed to describe the neurovascular coupling. This work formulates a novel low-rank plus multivariate sparse paradigm free mapping (LR+MV-SPFM) algorithm that disentangles neuronal-related BOLD signal fluctuations from global signal changes.

Theory

Signal Model: The whole-brain fMRI data $$$Y \in \mathbb{R}^{T \times V}$$$ with $$$T$$$ volumes and $$$V$$$ voxels can be decomposed into: $$$\mathbf{Y} = \mathbf{HS} + \mathbf{L} + \mathbf{N}$$$, where the neuronal-related component $$$\mathbf{H}\mathbf{S}$$$ is the convolution of voxel-specific neuronal-related signals $$$\mathbf{S} \in \mathbb{R}^{T \times V}$$$ with the Toeplitz matrix $$$\mathbf{H} \in \mathbb{R}^{T \times T}$$$ with shifted HRFs⁹.
LR+MV-SPFM solves the following optimization problem¹⁰:
$$\mathbf{\hat{L}}, \mathbf{\hat{S}} = \arg \min_{\mathbf{L}, \mathbf{S}} \| \mathbf{Y} - \mathbf{HS} - \mathbf{L} \|_F^2 + \lambda_L \| \mathbf{L} \|_* \\ + (1 - \rho) \|\mathbf{D}_S \mathbf{S} \|_{2,1} + \rho \| \mathbf{D}_S \mathbf{S} \|_1,$$
where $$$\mathbf{L} = \sum_{p=1}^{P}\mathbf{v}_p\mathbf{a}_p^T $$$: $$$\mathbf{v}_p \in \mathbb{R}^{T \times 1}$$$ and $$$\mathbf{a}_p \in \mathbb{R}^{V \times 1}$$$ denote the spatial and temporal signatures of $$$P$$$ low-rank (LR) components, and $$$\mathbf{N}$$$ denotes white Gaussian noise. $$$\ell_{2,1}+\ell_{1}$$$ enforces temporal sparsity and spatial structure on $$$\mathbf{S}$$$ and $$$\rho$$$ controls the tradeoff between both terms¹¹, $$$\mathbf{D}_s=\text{diag}\left(\lambda_{S_1},\ldots,\lambda_{S_V} \right)$$$ is a diagonal matrix with voxel-specific regularization parameters ($$$\lambda_{S_i} > 0$$$) balancing the sparsity of $$$\mathbf{S}$$$ and data fidelity, and the nuclear-norm $$$\|\cdot\|_*$$$ encourages the estimation of LR components where $$$\lambda_L > 0$$$ controls the number of components. $$$\rho=0.8$$$ enforces structure in the spatial domain and maintains the sparsity of estimates. $$$λ_{S_i}$$$ is the MAD estimate of the noise standard deviation after wavelet decomposition (Daubechies, order 3). After singular value decomposition, $$$\lambda_L$$$ selects $$$P$$$ LR components corresponding to the largest eigenvalues (difference $$$\geq10\%$$$ with respect to the next eigenvalue). This problem is solved via monotone FISTA with variable acceleration¹².

Methods

Simulations: 1000 voxels comprising two groups of 50 voxels with a known BOLD signal and 900 voxels with no BOLD signal, which were corrupted with different noise sources (motion-related, gaussian, and physiological noise)⁹ and two global LR components with a random voxelwise amplitude (two deep breaths⁸ and motion-related spikes) (Figure 1A). This data was analyzed with the proposed LR+MV-SPFM algorithm, and compared with its counterparts without modeling LR components (MV-SPFM), and without multivariate formulation (i.e. SPFM using $$$\rho=1$$$).
Experimental data: T2*-weighted multi-echo fMRI data of nine healthy subjects acquired on a 3T MR scanner (Siemens) with a multiband multi-echo gradient echo-planar imaging sequence (340 scans, 52 slices, Partial-Fourier=6/8, voxel-size=2.4x2.4x3mm3, TR=1.5s, TEs=10.6/28.69/46.78/64.87/82.96ms, flip-angle=70, MB factor=4, GRAPPA=2). Task: five randomly-intermixed movements (left-hand finger-tapping, right-hand finger-tapping, moving left toes, moving right toes, and moving the tongue). Preprocessing: head motion realignment, geometric distortion correction, and T2*-based optimal combination¹³ using TEDANA¹⁴.

Results

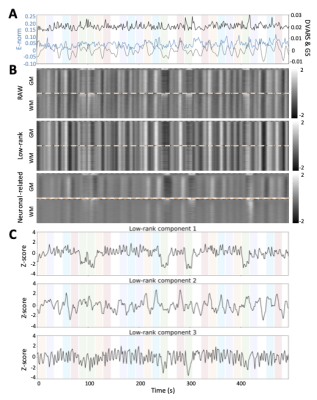
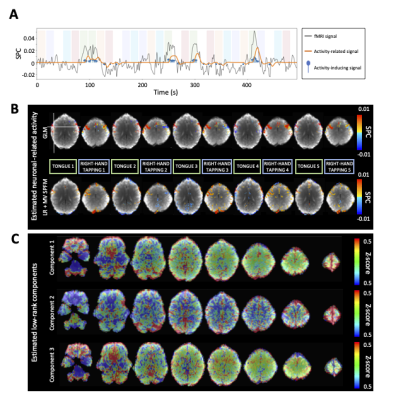
ROC curves in Figure 1B demonstrate that, regardless of the simulated SNR and BOLD/total voxels ratios, LR+MV-SPFM is more specific and provides higher sensitivity than the original SPFM method with Bayesian Information Criterion (BIC)9, except for the highest BOLD/total number of voxels ratio and highest SNR where a multivariate formulation seems to prevent the algorithm from fitting accurately at the voxel level. Figure 1C plots the error of the LR component estimate obtained with LR+MV-SPFM, showing that component estimation improves with higher percentage of voxels including only global signals.
Figures 2A-C depict the results of LR+MV-SPFM in a representative dataset. For this subject, the proposed approach estimated $$$P=3$$$ LR components (time-series and spatial maps in Figures 2C and 3C). Component 1 captures head-movement fluctuations and susceptibility artefacts during the ’moving the tongue’ condition, suggesting the subject moved the head while performing this task. Component 2 time-series closely follows the GS and its spatial map delineates major arteries and draining veins that strongly contribute to the GS. Component 3 captures global physiological fluctuations. LR+MV-SPFM detects neuronal-related signals at the trials’ timing (Figure 3A for tongue and right-hand finger-tapping) and the corresponding maps (Figure 3B) resemble those inferred with GLM ($$$p<0.001$$$). For example, the maps during the tongue trials depict tongue areas of the motor cortex bilaterally, even considering Component 1 also described global signal changes related to the tongue condition. Figure 4 depicts the ROC curves of LR+MV-SPFM ($$$\rho=0.8$$$), MV-SPFM and SPFM using the single-trial GLM activation maps as ground-truth. MV-SPFM and LR+MV-SPFMs provide higher sensitivity at the cost of reduced specificity.

Conclusion

LR+MV-SPFM allows reducing the effect of widespread signal changes to obtain accurate estimates of single-trial neuronal-related events. Our evaluations in simulations and real fMRI data demonstrated moderately improved deconvolution of neuronal-related activity in both simulations and real fMRI during a block-design motor task. Future work will include evaluation on event-related paradigms and resting-state, robust selection of regularization parameters¹⁵ and extending the proposed formulation for multi-echo acquisitions¹⁶ and describing the neuronal-related signal in terms of its innovation signals^17,18.

Acknowledgements

This work was supported by the European Union’s Horizon 2020 research and innovation program (Marie Skłodowska-Curie grant agreement No. 713673), La Caixa Foundation (ID 100010434, fellowship code LCF/BQ/IN17/11620063), the Spanish Ministry of Economy and Competitiveness (RYC-2017-21845), the Basque Government (BERC 2018-2021, PIBA_2019_104, PRE_2019_1_0054), the Spanish Ministry of Science, Innovation and Universities (PID2019-105520GB-100).

References

[1] Power, J.D., Plitt, M., Laumann, T.O. and Martin, A., 2017. Sources and implications of whole-brain fMRI signals in humans. Neuroimage, 146, pp.609-625.

[2] Caballero-Gaudes, C. and Reynolds, R.C., 2017. Methods for cleaning the BOLD fMRI signal. Neuroimage, 154, pp.128-149.

[3] Petridou, N., Gaudes, C.C., Dryden, I.L., Francis, S.T. and Gowland, P.A., 2013. Periods of rest in fMRI contain individual spontaneous events which are related to slowly fluctuating spontaneous activity. Human brain mapping, 34(6), pp.1319-1329.

[4] Allan, T.W., Francis, S.T., Caballero-Gaudes, C., Morris, P.G., Liddle, E.B., Liddle, P.F., Brookes, M.J. and Gowland, P.A., 2015. Functional connectivity in MRI is driven by spontaneous BOLD events. PloS one, 10(4), p.e0124577.

[5] Gonzalez-Castillo, J., Caballero-Gaudes, C., Topolski, N., Handwerker, D.A., Pereira, F. and Bandettini, P.A., 2019. Imaging the spontaneous flow of thought: Distinct periods of cognition contribute to dynamic functional connectivity during rest. NeuroImage, 202, p.116129.

[6] Bommarito, G., Tarun, A., Farouj, Y., Preti, M.G., Petracca, M., Droby, A., El Mendili, M.M., Inglese, M. and Van De Ville, D., 2020. Functional network dynamics in progressive multiple sclerosis. medRxiv.

[7] Tarun, A., Wainstein-Andriano, D., Sterpenich, V., Bayer, L., Perogamvros, L., Solms, M., Axmacher, N., Schwartz, S. and Van De Ville, D., 2020. NREM sleep stages specifically alter dynamical integration of large-scale brain networks. iScience, p.101923.

[8] Power, J.D., Plitt, M., Gotts, S.J., Kundu, P., Voon, V., Bandettini, P.A. and Martin, A., 2018. Ridding fMRI data of motion-related influences: Removal of signals with distinct spatial and physical bases in multiecho data. Proceedings of the National Academy of Sciences, 115(9), pp.E2105-E2114.

[9] Caballero Gaudes, C., Petridou, N., Francis, S.T., Dryden, I.L. and Gowland, P.A., 2013. Paradigm free mapping with sparse regression automatically detects single‐trial functional magnetic resonance imaging blood oxygenation level dependent responses. Human brain mapping, 34(3), pp.501-518.

[10] Otazo, R., Candes, E. and Sodickson, D.K., 2015. Low‐rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magnetic resonance in medicine, 73(3), pp.1125-1136.

[11] Gramfort, A., Strohmeier, D., Haueisen, J., Hamalainen, M. and Kowalski, M., 2011, July. Functional brain imaging with M/EEG using structured sparsity in time-frequency dictionaries. In Biennial International Conference on Information Processing in Medical Imaging (pp. 600-611).

[12] Zibetti, M.V.W., Helou, E.S., Regatte, R.R. and Herman, G.T., 2018. Monotone FISTA with variable acceleration for compressed sensing magnetic resonance imaging. IEEE transactions on computational imaging, 5(1), pp.109-119.

[13] Posse, S., Wiese, S., Gembris, D., Mathiak, K., Kessler, C., Grosse‐Ruyken, M.L., Elghahwagi, B., Richards, T., Dager, S.R. and Kiselev, V.G., 1999. Enhancement of BOLD‐contrast sensitivity by single‐shot multi‐echo functional MR imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 42(1), pp.87-97.

[14] DuPre, E., Salo, T., Markello, R., Kundu, P., Whitaker, K., Handwerker, D. ME-ICA/tedana: 0.0.9a. Zenodo; 2020. Available from: https://doi.org/10.5281/zenodo.3786890

[15] Uruñuela, E., Jones, S., Crawford, A., Shin, W., Oh, S., Lowe, M. and Caballero-Gaudes, C., 2020, July. Stability-Based Sparse Paradigm Free Mapping Algorithm for Deconvolution of Functional MRI Data. In 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC) (pp. 1092-1095). IEEE.

[16] Caballero-Gaudes, C., Moia, S., Panwar, P., Bandettini, P.A. and Gonzalez-Castillo, J., 2019. A deconvolution algorithm for multi-echo functional MRI: Multi-echo Sparse Paradigm Free Mapping. NeuroImage, 202, p.116081.

[17] Karahanoğlu, F.I., Caballero-Gaudes, C., Lazeyras, F. and Van De Ville, D., 2013. Total activation: fMRI deconvolution through spatio-temporal regularization. Neuroimage, 73, pp.121-134.

[18] Cherkaoui, H., Moreau, T., Halimi, A. and Ciuciu, P., 2019, May. Sparsity-based blind deconvolution of neural activation signal in fMRI. In ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (pp. 1323-1327). IEEE.

Figures

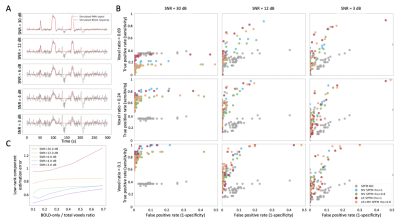
Figure 1: Simulation results. A) Example of simulated signals for different SNR conditions; B) ROC curves for the estimation of the neuronal-related signal with: SPFM using BIC (SPFM BIC), SPFM with no LR estimation and no spatial regularization (SPFM, $$$ \rho=1$$$), MV-SPFM with no LR estimation (MV-SPFM, $$$ \rho=0.8$$$), the LR+MV-SPFM algorithm with only the L1-norm (LR+SPFM, $$$ \rho=1$$$), and the LR+MV-SPFM algorithm ($$$ \rho=0.8$$$). C) Estimation error of the LR components for different ratios of BOLD/total number of voxels.

Figure 2: A) Euclidean norm of the motion displacements (E-norm) (blue), DVARS (black) and global (grey) signals of the fMRI data; B) Grayplots of grey matter (GM) and white matter (WM) of the preprocessed fMRI data, the estimated low-rank and neuronal-related components; C) time-series and of the estimated low-rank components.

Figure 3: A) Preprocessed fMRI and estimated neuronal-related Time-series in a voxel in the tongue motor area (see cross in map); B) single-trial GLM maps ($$$p<0.001$$$)and LR+MV-SPFM activation maps and C) maps of the three estimated low-rank components. The colour bands in the plots with time-series denote the timing of the different conditions.

Figure 4: ROC curves of the detection of neuronal-related activity at the times of the single trials for the five conditions for the three algorithms tested: SPFM, MV SPFM, and LR+MV SPFM. Each point represents a single trial event (9 subjects x 5 trials/condition). The darker points indicate the trials depicted in Figure 3.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

2685