Purpose

Conventionally in MRI, respiratory motion leads to shifts of tissue position in the image domain that correspond to linear phase errors in k-space. For segmented acquisitions, each k-space segment corresponds to a unique breathing-induced position shift, and a corresponding linear phase correction can be applied to each segment of k-space to perform motion compensation¹. Image-based navigators are one method to estimate the per-segment position shift and corresponding linear phase correction². For displacement encoding with stimulated echoes (DENSE), here we show that in addition to the position shift, respiratory motion (assumed to be rigid) leads to a phase shift in the image domain, which corresponds to a constant phase error in k-space. Thus, to perform motion compensation for segmented DENSE, per-segment linear and constant phase corrections must be computed and applied. Because DENSE typically employs both in-plane displacement-encoding gradients and through-plane dephasing gradients³, constant phase errors may arise from both in-plane and through-plane respiratory motion, which presents challenges to an iNAV-based approach. Using simulations, we show the feasibility of deep learning (DL) to compute the linear and constant phase corrections and to perform motion correction.

Theory

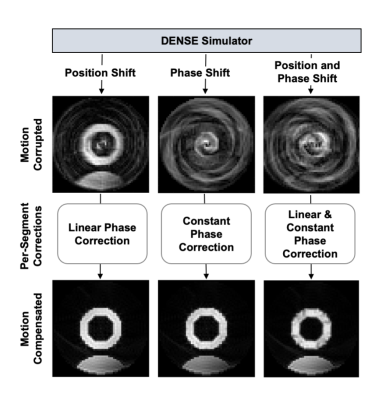
The displacement-encoded stimulated echo in DENSE is described in Equation 1: $$$M_{DE}=\ M(x)\ e^{-j2\pi k_e \Delta x_c}$$$ where the signal phase is proportional to the product of the displacement-encoding frequency, k_e, and the myocardial displacement, Δx_c⁴. The effect of displacement due to respiratory motion (Δx_R) leads to Equation 2: $$$\ M_{DE}^R=\ M\left(x-\Delta x_R\right)e^{-j2\pi k_e\Delta x_c}\ e^{-j2\pi k_e\Delta x_R}$$$ which accounts for both the shifted position of the magnetization as well as the phase shift resulting from displacement encoding of Δx_R. The position and phase shifts due to respiratory motion in the image domain lead to linear and constant phase errors, respectively, in k-space. For a segmented DENSE acquisition, the respiratory-corrupted signal, S, can be written as in Equation 3: $$$S(x)=\sum_{i=1}^{L}{F^HU_iF\ M_{DE}^{R_i}}$$$ , where F is the Fourier transform, L is the number of segments, U_i is the sampling function of the i^th segment, and H is the Hermitian transpose operator. Equation 4: $$$S_{mc}(x)=\sum_{i=1}^{L}{F^H\left[e^{j2\pi\ k\Delta x_{R_i}}e^{j{2\pi\phi}_i}\ \left(U_iFM_{DE}^{R_i}\right)\right]}$$$ shows how per-segment linear and constant phase corrections can be applied in k-space to correct respiratory-induced artifacts of the displacement-encoded stimulated echo, where k is the independent spatial frequency variable, Δx_R is the slope of the linear phase error, φ_i is the constant phase error, and S_mc is the motion-compensated image. This idea is demonstrated in Figure 1, where we used a computational deforming-heart phantom and Bloch equation simulations of the stimulated echo. The position of the phantom was shifted over time using a sine wave to simulate respiratory motion during imaging. Blurring and signal cancellation artifacts due to motion-induced position and phase shifts are shown in Figure 1, as are motion-compensated images computed using the motion correction of Equation 4. We postulated that DL would provide effective motion compensation for respiratory-corrupted DENSE, and we pursued this idea using computer simulations.

Methods

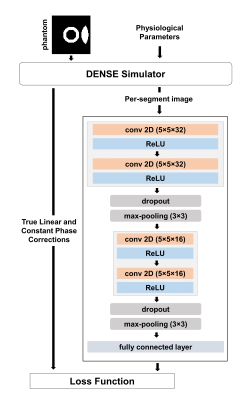
A Bloch-equation-based DENSE simulator was used to simulate free-breathing acquisitions of a computational deforming heart phantom. Respiratory motion was simulated using a sine wave. Training data were generated by varying the respiratory period, motion magnitude and initial phase in the ranges 15-25 cycles/min, 0-15 mm, and 0-0.5 cycles, respectively. A spiral cine DENSE acquisition with the following parameters was simulated: in-plane spatial resolution of 2.5×2.5 mm², balanced 3-point displacement encoding with displacement encoding frequency of 0.06 cyc/mm, 4 spiral interleaves per image with 1 interleaf acquired per heartbeat. We used 21,600, 4,800 and 2,400 simulated images for training, testing and validation, respectively. An encoder-type convolutional neural network (CNN) with two convolutional layers was implemented to estimate the linear and constant phase corrections. Max-pooling and dropout are followed after each convolutional layer and a fully connected layer is used as final layer. A diagram of the CNN and its training is illustrated in Figure 2. After training, per-segment linear and constant phase corrections were estimated using the CNN for the images in the test set. The corrections were implemented using Equation 4. The normalized difference (ND) defined in Equation 5: $$$ND\ =\frac{\left|\phi_{estimated}\right|-\left|\phi_{truth}\right|}{\phi_{truth}^{max}-\phi_{truth}^{min}\ \ }$$$ was used to quantify the accuracy of estimations compared to the ground-truth values.

Results

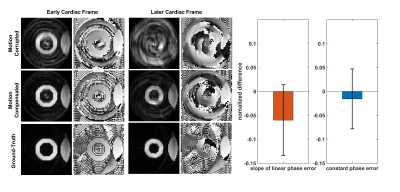
Figure 3 shows examples of Bloch-equation-simulated motion-corrupted DENSE images and their corresponding motion-compensated images (compensated using Equation 4 with CNN-derived phase correction values), as well as the ground-truth images. Two examples are shown: one from an early cardiac frame where the effect of the constant phase error is insignificant and another from a later cardiac frame where both artifact types are significant. The plots of ND show that the CNN computed phase correction values within approximately 6% and 2% of the true values.

Discussion

We developed a new motion model to describe the effects of respiratory motion in DENSE imaging. The model incorporates the respiratory-motion-induced phase shift of the stimulated echo, in addition to the position shift which is common to all MRI. Further, we showed the potential of DL as a method for performing motion compensation. Further work will augment the training data with vivo DENSE images and evaluate the method for in vivo DENSE imaging.

Acknowledgements

This work was supported by R01HL147104.