2660
Deep learning-based reconstruction for 3D coronary MR angiography with a 3D variational neural network (3D-VNN)
Ioannis Valasakis1, Haikun Qi1, Kerstin Hammernik2, Gastao Lima da Cruz1, Daniel Rueckert2,3, Claudia Prieto1, and Rene Botnar1
1King's College London, London, United Kingdom, 2Technical University of Munich, Munich, Germany, 3Imperial College London, London, United Kingdom
1King's College London, London, United Kingdom, 2Technical University of Munich, Munich, Germany, 3Imperial College London, London, United Kingdom
Synopsis
3D whole-heart coronary MR angiography (CMRA) is limited by long scan times. Undersampled reconstruction approaches, such as compressed sensing or low-rank methods show promise to significantly accelerate CMRA but are computationally expensive, require careful parameter optimisation and can suffer from residual aliasing artefacts. A 2D multi-scale variational network (VNN) as recently proposed to improve image quality and significantly shorten the reconstruction time. We propose to extend the VNN reconstruction to 3D to fully capture the spatial redundancies in 3D CMRA. The 3D-VNN is compared against conventional and 3D model-based U-Net reconstruction techniques, showing promising results while shortening the reconstruction time.
Introduction
3D whole-heart coronary MR angiography (CMRA) has shown great potential to non-invasively diagnose coronary artery disease but is still limited by long scan times. Undersampled reconstruction approaches, such as compressed sensing (CS)1 or patch-based low-rank reconstruction2 methods show promise to significantly accelerate CMRA but are computationally expensive, require careful hyperparameter optimisation and can suffer from residual aliasing artefacts. Recently, a 2D multi-scale Variational Network (VNN)3,4 was proposed to improve image quality and significantly shorten the reconstruction time. Here we propose to extend the Variational Network to 3D (3D-VNN) to fully capture the spatial redundancies in 3D CMRA. The 3D-VNN is compared against conventional CS, iterative SENSE (itSENSE) and 3D model-based (MoDL)5 U-Net reconstruction techniques, showing promising results while shortening the reconstruction time to ~15s for a 5-fold accelerated scan of ~2-4 minutes.Methods
Acquisition: Free-breathing 3D CMRA data were acquired from 18 healthy subjects and 1 patient, using a 1.5T MRI scanner (Aera, Siemens Healthineers) with 1.2 mm3 isotropic resolution using a variable-density Cartesian spiral-like trajectory (VD-CASPR) and iNAV6 for translational respiratory motion correction (Fig.1A) as described before in Fuin et al4. CMRA acquisitions were performed fully sampled (average acq. time in (mm:ss) (AT) = 18:55) and for the 5-fold (AT = 04:11) acceleration. Training was done with 14 subjects with retrospective undersampling. Two subjects with prospective and retrospective undersampling were considered for validation, whereas 3 subjects (2 healthy and 1 patient) with 5-fold prospective undersampling were considered for testing and evaluation.3D-VNN for CMRA: The architecture of the 3D-VNN is shown in Fig. 1B and uses the motion-corrected raw data and the corresponding coil sensitivity maps (CSM) as input. Translational motion correction was applied (Fig. 1A) and the undersampling readout was removed. Coil were compressed to 18 virtual coils using geometrical decomposition coil compression and CSMs were estimated using ESPIRiT from BART toolkit. The 3D-VNN consists of two streams: one to enforce data consistency (DC) of the motion-corrected undersampled k-space data and the second stream, which is a regularisation operator that applies real-valued 3D filter kernels and can be defined as a 3D Fields of Experts model (Fig 1B). Linear activation functions (LAF) are applied to the real and imaginary part of the complex-valued 3D image. LAFs allow for faster reconstructions as it eliminates the need for the computationally expensive pairwise distance calculation of the intensity of the image. The unrolled scheme is updated in each iteration (Fig 1B) with the learning rate η(t), Φ(x) the gradient of the regularisation function with respect to the image x and k the multi-channel translational motion-compensated k-space measurements and φ the linear activation functions which combine the two-plane filter responses. The data consistency is enforced to the translational motion-compensated undersampled k-space data by applying the linear sampling operator A* which combines a forward fast Fourier transform (FFT) operator and a point-wise multiplication with the CSMs. The size of the 3D kernels and activation functions was set to 7x7x7 and 36 respectively after optimisation and the 3D filter kernels allow the network to learn the spatial structures and characteristics of the CMRA images. The 3D-VNN has 166731 learnable parameters for all the filter layers and the 3D U-Net has 86531. The 3D U-Net model was trained by using overlapping 3D volumes (“slabs”) which allowed for training to be performed in a GPU with less memory thus allowing training on available hardware. Using the whole volume, in that case, could be prohibitive without GPU with a very large memory capacity. The loss function is computed as the mean squared error between the 3D-VNN reconstruction and the fully sampled datasets. A conjugate gradient (CG) model-based (MoDL)5 with U-Net regularization (Fig. 2) was employed for comparison purposes. The 3D-VNN was also compared against CS and itSENSE reconstructions.
Results
The 3D-VNN allowed a fast reconstruction of good quality CMRA images from 5-fold undersampled datasets showing comparable or superior image quality compared to CS and itSENSE reconstruction with a significantly shorter reconstruction time of ~15s compared to 2.5 minutes for CS and 2 minutes for itSENSE (Figure 3). 3D-VNN image quality was comparable to the CG-MoDL U-Net while the reconstruction time of the latter was ~1.5 minutes when volumetric reconstruction was performed and ~13.5s when reconstruction was done using slabs. For quantitative comparison of the image quality obtained with the different reconstruction techniques, PSNR (dB) was calculated from a ROI covering the heart: 21.2 (ZF), 31.8 (CS), 32.5 (3D U-Net) and 32.8 (3D-VNN). The trainable network parameters for the 3D U-Net were 86531 and 166731 for the 3D-VNN resulting in a training time of ~46 hours for the 3D U-Net and ~5 days for the 3D-VNN for a RAM of 128GB and an NVIDIA TITAN V GPU with 11GB.Conclusion
Leveraging an unrolled optimisation scheme, the 3D-VNN reconstruction shows promise to provide good quality visualisation of the cardiac and coronary anatomy with CMRA obtained from a ~2-4 min scan and with a very short reconstruction time of 15s, showing promise for the utilisation in a clinical workflow.Acknowledgements
This work was supported by the following grants: (1) EPSRC EP/P032311/1, EP/P001009/1 and EP/P007619/1, (2) BHF programme grant RG/20/1/34802, (3) King’s BHF Centre for Research Excellence RE/18/2/34213 (4) Wellcome EPSRC Centre for Medical Engineering (NS/A000049/1).References
- Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007 Dec;58(6):1182-95. doi: 10.1002/mrm.21391
- Bustin A, Ginami G, Cruz G, Correia T, Ismail TF, Rashid I, Neji R, Botnar RM, Prieto C. Five-minute whole-heart coronary MRA with sub-millimetre isotropic resolution, 100% respiratory scan efficiency, and 3D-PROST reconstruction. Magn Reson Med. 2018. doi: 10.1002/mrm.27354.
- Hammernik, Kerstin & Klatzer, Teresa & Kobler, Erich & Recht, Michael & Sodickson, Daniel & Pock, Thomas & Knoll, Florian. (2017). Learning a Variational Network for Reconstruction of Accelerated MRI Data. Magnetic Resonance in Medicine. 79. 10.1002/mrm.26977.
- Fuin, N., A. Bustin, Thomas Küstner, Ilkay Oksuz, J. Clough, A. King, Julia Schnabel, R. Botnar and C. Prieto. “A multi-scale variational neural network for accelerating motion-compensated whole-heart 3D coronary MR angiography.” Magnetic resonance imaging (2020): doi:10.1016/j.mri.2020.04.007
- H. K. Aggarwal, M. P. Mani and M. Jacob, "MoDL: Model-Based Deep Learning Architecture for Inverse Problems," in IEEE Transactions on Medical Imaging, vol. 38, no. 2, pp. 394-405, Feb. 2019, doi: 10.1109/TMI.2018.2865356.
Figures
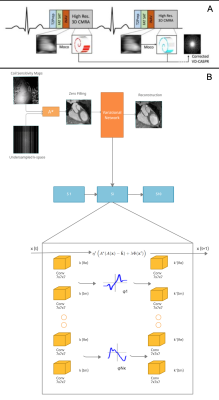
(A) The CMRA data acquisition and motion correction pipeline using a VD-CASPR trajectory and performing translational motion correction estimated from 2D iNAVs. (B) CSMs and the undersampled k-space data are used as network inputs. The variational network structure for one gradient step: the filters k are learned for the real and complex plane and a linear activation function combines the responses of the filters on those planes. The loss function is the MSE of the 3D-VNN reconstruction and the fully sampled.
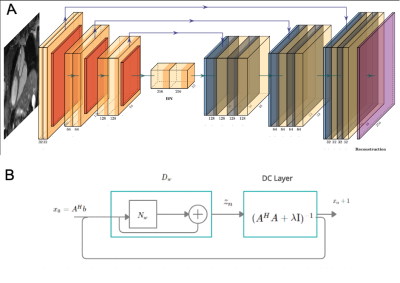
(A) The architecture of the 3D CG MoDL-U-Net receiving as input the 3D slabs of size 32x32x3. A conjugate gradient optimiser block is used with a recursive structure which has a cyclic repetition between the denoiser Dw, Dn and a data consistency (DC) layer, as shown in (B) where Nw is an estimator of noise and alias learned by the network, x the image and A = SF with S the sampling operator and F the Fourier transform. Dw is the denoised estimate and here it is interpreted as a residual learning network.
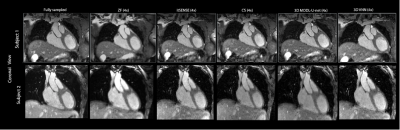
CMRA reconstructions for 5-fold undersampling for two representative subjects. 3D-VNN reconstruction is compared against the CS, iterative SENSE, CS and 3D CG MoDL-U-Net for a representative subject. Fully sampled and zero-filled reconstructions are also included for comparison.