Introduction

Non-gated real-time cardiac imaging requires reconstructing dynamic images sequence from highly undersampled k-t space data. Classical model-based methods exploit transform sparsity and spatial-temporal correlations^1-3 to solve this ill-posed inverse problem. However, these methods usually contain a time-consuming optimization process with many iterations, which hinders their application in clinical practice. Recently, a model-based deep-learning framework named “variational network” (VN)^4,5 manifests its capability to unroll iterative process and accelerate convergence. In this study, we incorporated the classical “partial separable” (PS) model⁶ into VN’s framework for real-time cardiac imaging, named PS-VN, which achieves comparable reconstruction accuracy with baseline algorithms and much faster computational speed.

Methods

Reconstruction Method
The most time-consuming step in traditional PS model algorithm is to solve spatial basis images $$$U$$$: $$\min_{U}{\parallel{M{\circ}FS(UV)-b}\parallel}_2^2$$
where the notations denote: temporal basis functions $$$V$$$, coil sensitivity maps $$$S$$$, Fourier transform matrix $$$F$$$, undersampling mask $$$M$$$, acquired k-space data $$$b$$$.
In our PS-VN architecture, we define $$$A$$$ as an encoding operator which maps $$$U$$$ to k-space data: $$A(U)=M{\circ}FS(UV)$$
and reformulate the optimization objective as follows: $$\min_{U}{\parallel{AU-b}\parallel}_2^2+\psi(KU)$$
where $$$K$$$ is 3D convolution kernel and $$$\psi$$$ is tunable activation function controlled by linear interpolation knots⁵.
The gradients takes the following formulation: $$grad(U)=A^HAU-A^Hb+K^H\psi'(KU)$$
where $$$A^H$$$ denotes the adjoint operator, $$$\psi'$$$ denotes the derivative of the activation function.
We use VN framework to unroll this iterative process. An iteration step corresponds to a VN layer, which consists of two blocks: a data fidelity block, which implements the $$$A^HAU-A^Hb$$$ operation; and a regularization block, which implements $$$K^H\psi'(KU)$$$ operation.
The $$$i$$$-th layer of PS-VN layer updates spatial basis images $$$U$$$ as follows: $$U^{(i)}=U^{(i-1)}-(A^HAU^{(i-1)}-A^Hb+K_i^H\psi_i'(K_iU^{(i-1)}))\,\,\,\,\,\,\,(i=1,......,N)$$
where $$$i$$$ is the layer index. $$$N$$$ denotes the total number of VN layers.
The network loss is computed as a weighted sum of L1-norm of reconstructed error of each layer: $$Loss(U)=\sum_{i=1}^Ne^{-\tau(N-i)}{\parallel{U^{(i)}V-X^*}\parallel}_1$$
where $$$\tau$$$ is a constant used for weighting loss from different layers, $$$X^*$$$ is the ground truth image.
Figure 1 demonstrates the overall PS-VN reconstruction method pipeline.

Data acquisition and experiment setup
We implemented an ECG-gated cardiac CINE acquisition on a 3T MR scanner (Philips Achieva TX, Best, Netherland) to perform the retrospective phantom experiment. Imaging parameters were: SPGR sequence with TFE factor=12, field of view 300x261mm², acquisition matrix size=110x304, spatial resolution=2x2.4mm², slice thickness=8mm, flip angle 15°, TR/TE=5.5/3.3ms, heart phases=24.
The CINE k-space data were prolonged and reordered to simulate a sequence of 4400 frames. The ground truth images were acquired by directly applying iFFT to the CINE data and then coil combination by SOS algorithm. Simulated acquisitions were performed based on PS alternating sampling trajectory to produce training data and highly undersampled (R=110) imaging data⁷. Imaging data was then compressed by GCC algorithm⁸ to 6 virtual coil channels. $$$S$$$ was caluculated from imaging data. Training data was preprocessed according to PS model to calculate $$$V$$$.
Due to big data size of this problem (110x304x4400 per slice), large data set is difficult to acquire and computationally inhibitive. Therefore, we divided the data into (110x304x200) batches. We accumulated the gradient and updated parameters every 21 bacthes (4200 frames) to simulate the PS model iterative scenario, thus each raw data could generate 201(4400-4200+1) effective data samples. By this data augmentation method, a dataset containing 2814 data samples (110x304x4200) was established from 14 raw slice data which were acquired from 2 volunteers. 2412(6/7) samples were used as training set, validation set and test set contained 201(1/14) samples respectively.

Results evaluation
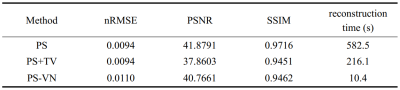
PS model reconstruction method was used as the baseline method. PS model rank (L=15) was selected manually. In addition, algorithm based on PS model plus total variation constraints (PS+TV) was also implemented for comparision. nRMSE, PSNR, SSIM and reconstruction time were evaluated. SSIM indexes were calculated over a ROI region containing the heart.

Results

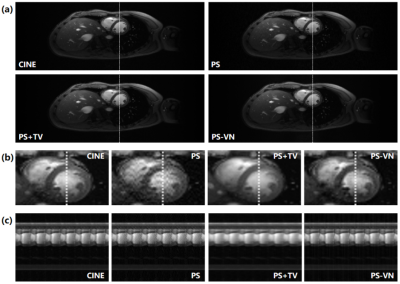
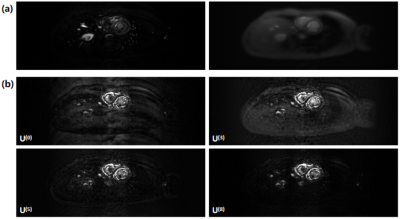
Table 1 summarizes the evaluated metrics of different reconstruction methods. PS-VN achieves a comparable accuracy with the baseline method and consumes only around 10 seconds for reconstruction of 4200 frames. Figure 2 shows example reconstructed images of different algorithms. PS-VN avoids the fluctuating artifacts in PS and temporal smoothing effects in PS+TV, displaying better visual image quality. Figure 3 shows the updating gradient images produced by a VN layer and the iterative process of U through the PS-VN network, which provides more insights into our reconstruction method.

Discussion and Conclusion

The basic idea behind this method is actually general. We formulated the problem solved by VN as searching iterative shortcuts in the high-dimensional solution space. The underlying assumption is that the heavily corrupted images actually share common aliasing patterns. Though tough to be recognized, these patterns may be learned by variational network framework. Therefore, reconstruction can be achieved by following these shortcuts instead of solving a high dimensional optimization problem. We believe this concept can also be applied to other iterative models to achieve accelerated convergence. We select classical PS model as the first attempt of this concept, because its acquisition utilizes regular Cartesian undersampling scheme which is believed to generate a hidden aliasing pattern. This pilot study preliminarily validates our idea, but more comprehensive study is needed. There also remains some technical problems to be solved, such as long training time of this method.

Acknowledgements

No acknowledgement found.