2650
Fast personalization of cardiac mechanical models using parametric physics informed neural networks1ETH Zurich, Zurich, Switzerland
Synopsis
We propose a parametric physics-informed neural network that can be personalized to left-ventricular anatomies from cardiac MRI data. The model combines a left-ventricular anatomical shape model derived from cardiac MRI data, and a functional model derived from synthetic cardiac deformations. The network is trained with a label-free approach using a physics-based cost-function in less than 5 minutes on a single CPU. Network inputs are endocardium pressure and myocyte activation. A complete cardiac cycle can be simulated in less than a minute. This approach is 30 times faster than the corresponding finite element simulation even when including training time.
Introduction
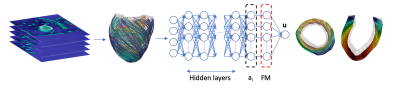
The personalization of a biomechanical model from MRI usually requires the identification of one or more parameters via multiple runs of computationally expensive numerical models [11,13]. Different abstraction levels can be used to balance the computational cost of the model against the level of detail. Lumped parameter models [5,6] and reduced-order models [3,4] are among the most common alternatives to full biomechanical simulations. Recently, neural networks have also been used to generate surrogate physical models in various fields [7-10,12,14]. The main disadvantages of approaches based on neural networks are long training times and the need for training data. We propose to alleviate these shortcomings by coupling a physics-informed neural network (PINN) with an anatomical left-ventricular shape model (SM) and a functional model (FM) describing cardiac deformations. The neural network is trained by minimizing an energy potential functional for hyperelastic, anisotropic, nearly-incompressible active materials. In this way we can simulate full cardiac cycles and avoid expensive simulations to generate training data for the network of each new patient. Selecting endocardium pressure and myocyte activation stresses as inputs, the PINN predicts the displacement of the nodes of the mesh defined by the SM. Training time is around 5 minutes on a single CPU after which cardiac deformations can be obtained as a function of the input parameter variability. The PINN is coupled with lumped parameter models of the circulation [2,16] to account for the interaction of cardiac function with systemic circulation and simulations are completed in less than 1 minute on standard computer hardware.Methods
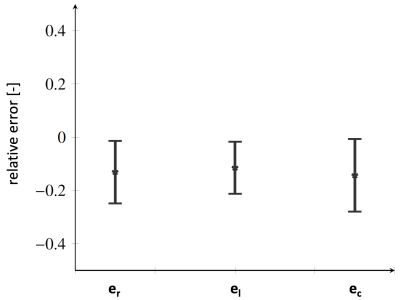
We use a left-ventricular shape model (SM) [2] to generate a dataset of 100 synthetic anatomies which are assumed to be in the end-systolic configuration at the lowest value of pressure in the cycle. After the selection of realistic boundary conditions, tissue stiffness and microstructures, a biophysical finite element (FE) model [2] is used to obtain a set of deformation fields. Applying Proper Orthogonal Decomposition (POD) on this deformation dataset gives the basis for the FM. The linear combination of the basis allows the reconstruction of the ventricular displacement up to an error determined by the number of FM bases considered. The FM basis defines the last layer of a dense neural network, schematically shown in Fig. 1, which is constrained to the biophysical problem in two ways: i) the network output is restricted to the subspace spanned by the FM bases and ii) the cost function used for training is the energy potential functional specifically tailored for hyperelastic, anisotropic, nearly-incompressible active materials.Sixty additional synthetic anatomies are generated with microstructure, material and circulation properties within the physiologically realistic ranges [2] for the 100 synthetic anatomies used for the generation of the FM. On each anatomy we train the PINN to simulate the corresponding cardiac function. The PINN is trained for 400 epochs using an Adam optimizer and a learning rate of 10-4 in TensorFlow [1]. Network width, depth and the number of FM bases were determined using a parametric study and we selected the swish [15] activation function for all cases. From this analysis we determined the network architecture with 5 layers, 5 hidden neurons per layers and 10 FM bases. On these 60 new anatomies, cardiac function was also simulated using a biophysical model [2] providing the ground truth for comparison. We compared global metrics such as prediction of ejection fraction, peak systolic pressure, stroke work and averaged radial, longitudinal and circumferential end-diastolic strains.
Results
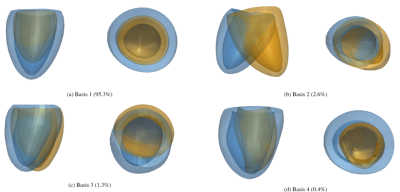
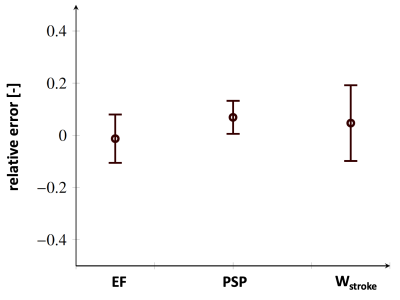
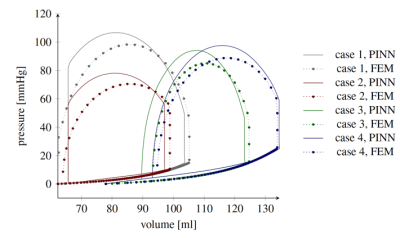
Figure 2 shows the impact on the mean anatomy of each individual SM basis weighted by the max and min values observed in the training dataset. Figures 3 and 4 show the error statistics (mean and standard deviation) on metrics of interest for the PINN (ejection fraction, peak systolic pressure, stroke work and physiological strains) as compared with ground truth values from the biophysical FEM model. In Figure 5 the pressure-volume loops predicted from the PINN for 4 different operative conditions are compared to those from the FE model. For each case, training and running times are 5 mins and 1 mins, respectively, on standard computer hardware.Discussion
In this work synthetically generated anatomies based on a shape model have been used. Although only few modes of variations were considered, the bases enabled generation of synthetic dataset with realistic variabilities. This approach allowed for the definition of anatomically consistent shapes and the calculation of functional models of the left ventricle which in turn was encoded in the last layer of a physics-informed neural network. The PINN was trained without labelled data using an energy cost function in less than 5 minutes on a CPU. The PINN was coupled to circulatory models and cardiac function predictions took less than 1 minute with averages predictions within 10% of the corresponding FEM model.Acknowledgements
No acknowledgement found.References
[1] Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., Corrado, G.S., Davis, A., Dean, J., Devin, M., Ghemawat, S., Goodfellow, I., Harp, A., Irving, G., Isard, M., Jia, Y., Jozefowicz, R., Kaiser, L., Kudlur, M., Levenberg, J., Man´e, D., Monga, R., Moore, S., Murray, D., Olah, C., Schuster, M., Shlens, J., Steiner, B., Sutskever, I., Talwar, K., Tucker, P., Vanhoucke, V., Vasudevan, V., Vi´egas, F., Vinyals, O., Warden, P., Wattenberg, M., Wicke, M., Yu, Y., Zheng, X., 2015. Tensor-Flow: Large-scale machine learning on heterogeneous systems. URL: https://www.tensorflow.org/. software available from tensorflow.org.
[2] Buoso, S., Joyce,T, Kozerke S, (Forthcoming). Personalising left-ventricular biophysical models of the heart using parametric physics-informed neural networks.
[3] Buoso, S., Manzoni, A., Alkadhi, H., Plass, A., Quarteroni, A., Kurtcuoglu, V., 2020b. Reduced-order modeling of blood flow for noninvasive functional evaluation of coronary artery disease. Biomechanics and Modeling in Mechanobiology 18, 1867–1881. doi:10.1007/s10237-019-01182-w.
[4] Buoso, S., Palacios, R., 2017. On-demand aerodynamics of integrally actuated membranes with feedback control. AIAA Journal 55, 377–388. doi:doi.org/10.2514/1.J054888.
[5] Caruel, M., Chabiniok, R., Moireau, P., Lecarpentier, Y., Chapelle, D., 2014. Dimensional reductions of a cardiac model for effective validation and calibration. Biomechanics and Modeling in Mechanobiology 13, 897–914. doi:10.1007/s10237-013-0544-6.
[6] Charlton, P.H., Mariscal Harana, J., Vennin, S., Li, Y., Chowienczyk, P., Alastruey, J., 2019. Modeling arterial pulse waves in healthy aging: a database for in silico evaluation of hemodynamics and pulse wave indexes. American Journal of Physiology-Heart and Circulatory Physiology 317, H1062– H1085. doi:10.1152/ajpheart.00218.2019.
[7] Fresca, S., Dede, L., Manzoni, A., 2020. A comprehensive deep learningbased approach to reduced order modeling of nonlinear time-dependent parametrized pdes. arXiv preprint arXiv:2001.04001.
[8] Hesthaven, J., Ubbiali, S., 2018. Non-intrusive reduced order modeling of nonlinear problems using neural networks. Journal of Computational Physics 363, 55 – 78. doi:doi.org/10.1016/j.jcp.2018.02.037.
[9] Lee, K., Carlberg, K.T., 2020. Model reduction of dynamical systems on nonlinear manifolds using deep convolutional autoencoders. Journal of Computational Physics 404, 108973. doi:doi.org/10.1016/j.jcp.2019.108973.
[10] Maso Talou, G.D., Babarenda Gamage, T.P., Sagar, M., Nash, M.P., 2020. Deep learning over reduced intrinsic domains for efficient mechanics of the left ventricle. Frontiers in Physics 8, 30. doi:10.3389/fphy.2020.00030.
[11] Mollero, R., Pennec, X., Delingette, H., Ayache, N., Sermesant, M., 2019. Population-based priors in cardiac model personalisation for consistent parameter estimation in heterogeneous databases. International Journal for Numerical Methods in Biomedical Engineering 35, e3158. doi:10.1002/cnm.3158.
[12] Nguyen-Thanh, V.M., Zhuang, X., Rabczuk, T., 2020. A deep energy method for finite deformation hyperelasticity. European Journal of Mechanics - A/Solids 80, 103874. doi:doi.org/10.1016/j.euromechsol.2019.103874.
[13] Pfaller, M.R., H¨ormann, J.M., Weigl, M., Nagler, A., Chabiniok, R., Bertoglio, C., Wall, W.A., 2019. The importance of the pericardium for cardiac biomechanics: from physiology to computational modeling. Biomechanics and Modeling in Mechanobiology 18, 503–529. doi:10.1007/s10237-018-1098-4
[14] Raissi, M., 2018. Deep hidden physics models:deep learning of nonlinear partial differential equations. Journal of Machine Learning Research 19.
[15] Ramachandran, P., Zoph, B., Le, Q.V., 2017. Searching for activation functions. arXiv preprint arXiv:1710.05941 .
[16] Westerhof, N., Lankhaar, J.,Westerhof, B., 2009. The arterial windkessel. Medical & biological engineering & computing 47, 131–141.
Figures