Introduction

Susceptibility Weighted Imaging (SWI)¹ is a useful technique with a broad range of clinical and research applications. Complex images of SWI are acquired with T2* weighted sequences using gradient echoes, in which the phase contains contributions from magnetic field inhomogeneity due to local tissue susceptibility variations as well as a smoothly varying background phase error. In SWI, the former is of interest and the latter is to be removed. Typically, this goal is achieved by taking advantage of their intrinsic properties, namely the spatial change of the latter is more gradual and smoother relative to the former. One approach used homodyne demodulation, where the complex image was first smoothed using a low-pass filter and resulting phase was removed as the background phase error¹. An alternative approach used a phase unwrapping operation followed by smoothing of the unwrapped phase map². The above methods work well in many cases but may be challenged when large phase loops are present in the data³. The very center of such phase loop is a pole (or singularity) where the phase value is undefined, similar to the undefined local time at the North and South Poles on Earth. When the complex image is smoothed at a pole, the result may become unstable, yielding erroneous background phase correction; On the other hand, correct phase unwrapping may be very difficult if not impossible at a large phase loop due to its peculiar topological structure similar to Penrose stairs⁴. In both cases, approximations are used as the background phase which may result in artifacts in the subsequent SWI contrast. In this work, an algorithm of background correction with phase diffusor (BACOPSOR) is introduced. Although involving only simple operations, it has the desirable immunity to large phase loops with center poles, and thus may offer improved results. With in vivo data, BACOPSOR has been demonstrated to be useful for Susceptibility Weighted Imaging.

Method

Theory: The phase map $$$\phi$$$ can be directly smoothed by a hypothetical diffusion process⁵ that satisfies the following equation,
$$\frac{\partial \phi}{\partial t}=D\triangledown^{2}\phi\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space(1)$$
where D is a constant diffusion coefficient. Using discrete temporal steps, a recursive expression can be obtained,
$$\phi_{n+1}=\phi_{n}+D\triangledown^{2}\phi_{n}\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space(2)$$
where the phase Laplacian includes spatial differentials as well as a phase wrapping operator W that returns a wrapped value within $$$[-\pi,+\pi)$$$. In 2D, the phase Laplacian $$$\triangledown^{2}\phi_{n} $$$ for a pixel at (x,y) is then found from itself and its 4-connected neighbors,
$$\triangledown^{2}\phi_{n}={W[\phi_{n}(x+1,y)-\phi_{n}]+W[\phi_{n}(x-1,y)-\phi_{n}]+W[\phi_{n}(x,y+1)-\phi_{n}]+W[\phi_{n}(x,y-1)-\phi_{n}]}\space\space\space\space\space(3)$$
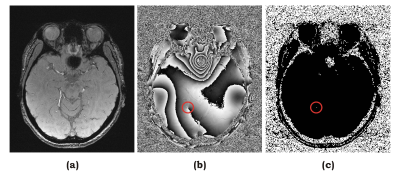
The same wrapping operator W is applied to all terms in Eq.(2) and Eq.(3) when they are added. The phase Laplacian $$$\triangledown^{2}\phi_{n} $$$ is set to zero at pixels on the pole mask³ as shown in Fig.1(c). After a total of N steps of iterations, a smooth background phase map can be obtained and removed from the original phase map.

Experiment: Complex in vivo brain images were acquired on a 3T scanner using a gradient-echo sequence, with matrix size = 430x510. Data were processed offline with the above algorithm for background error removal, on a laptop PC with a program written in C-language. The following parameters were used D=0.2, N=100.

Results

Figure 1 shows a representative slice of original complex image in magnitude (a) and phase (b) respectively. Figure 1(b) contains a large phase loop around a pole indicated by a red circle. This structure can be problematic for complex smoothing and phase unwrapping. A pole mask³ was readily generated as Fig.1(c). Figure 2(a) shows the original phase map processed by Eq.(2) after N=100 iterations. The phase is well smoothed representing the background phase error. The large phase loop was not affected by the diffusion process and thus can be removed altogether as well. Figure 2(b) shows resulting phase map after background correction when the phase of Fig.2(a) was removed from that of Fig.1(b), leaving a clean phase contrast only due to local susceptibility variations. For comparison, the original images in Fig.1 were also processed with complex smoothing. The circled pole has been shifted slightly to another location as shown in Fig.3(a). Figure 3(b) is result after phase subtraction of Fig.3(a) from Fig.1(b), a dipole has been created near the pole, and other artifacts can be seen in regions where the phase changed rapidly (arrows).

Discussion

BACOPSOR uses a phase Laplacian operator iteratively to perform phase diffusion that is able to smooth the phase map while keeping the large phase loops intact. The “phase flow” travels around the pole without changing its structure. When the diffused phase map obtained as such was subtracted from the original phase map, both the slow varying background and the large phase loops were simultaneously removed, yielding a clean desired phase contrast due to only local susceptibility variations. Diffusive phase evolution was previously used in pseudo-temporal phase unwrapping (PTPU)⁵ for flow velocity mapping. This approach may also be expected to find utility in other phase sensitive applications such as Dixon water-fat imaging⁶. Beyond 2D, BACOPSOR can also be readily implemented in higher dimensions.

Conclusion

An algorithm of background correction with phase diffusor (BACOPSOR) is described. Unlike other approaches such as complex smoothing and phase unwrapping, it is straightforward and robust as demonstrated with in vivo data for susceptibility weighted imaging.

Acknowledgements

No acknowledgement found.