Introduction

With multi-coil dynamic hyperpolarized MRI, dissolution dynamic nuclear polarization enhances the signal strength to greater than $$$10,000$$$ times its thermal equilibrium [1]. A sample is prepared and injected into a patient and then observed in vivo using MRI as it is converted through metabolism by the body's tissues [2]. It is often the case that the injected contrast agent is not dispersed enough throughout the field of view to get an accurate estimate of the sensitivity maps well, prohibiting the use of SENSE reconstruction methods. Instead, the most accurate method combines individual images from each coil [3]. A hardware modification can add fiducial markers into the coils, which then permits the estimate of sensitivity maps with the Biot-Savart law [4]. Without this modification, though, the lack of accurate sensitivity maps prohibits model based reconstructions. In this abstract, we discuss a method to reconstruct the individual images well so that they can be combined into an accurate reconstruction of the sample.

Methods

A solution containing 1.47 g of Good Manufacturing Practice (GMP) grade [1-$$$^{13}$$$C] pyruvic acid (Millipore Sigma Isotec) was hyperpolarized using a SPINlab polarizer (GE Healthcare) operating at 5 T and 0.8 K for 3 h. Once polarized and after preparing the solution for injection (including raising the solution to safe temperatures for the body) and release by a pharmacist, a 0.43 mL/kg dose of ~250 mM pyruvate was injected at a rate of 5 mL/s, followed by a 20 mL sterile saline flush (0.9\% sodium chloride, Baxter HealthcareCorporation). Cardiac gated imaging was accomplished with a 3T MR scanner (MR750, GE Healthcare) with a gradient performance of $$$50$$$ mT/m maximum gradient strength and $200$ T/m/s maximum slew-rate. Three metabolites (pyruvate, lactate, and bicarbonate) were individually excited using a single-band spectral-spatial excitation pulse designed using the Hyperpolarized MRI Toolbox [5]. Data was collected using a single-shot spiral trajectory for each metabolite; one image was acquired at approximately every $$$2$$$ seconds.Reconstructions of each metabolite were conducted individually. Since the image of each coil is the underlying image of the sample apodized by its smooth sensitivity map, much of the spatial structure in the images from different coils will be similar. This suggests that the joint sparsity of images captured at the same time from multiple coils, quantified using the $$$L_{2,1}$$$ norm, will be small [6,7]. Moreover, as with conventional dynamic MRI [8], in hyperpolarized MRI, the images from all times of a single coil are low rank [9]. Thus, we expect the nuclear norm of the appropriate matrix to be small.Let $$$x^{(t)}_{(c)}$$$ be the image at time $$$t$$$ from coil $$$c$$$ extended into a column vector. Let $$$X_{(c)} = [x^{(1)}_{(c)} \hspace{0.3em} x^{(2)}_{(c)} \hspace{0.3em} \cdots \hspace{0.3em} x^{(T)}_{(c)}]$$$ be the matrix formed by concatenating the image column vectors of all times from coil $$$c$$$. Similarly, let $$$X^{(t)} = [ x^{(t)}_{(1)} \hspace{0.3em} x^{(t)}_{(2)} \hspace{0.3em} \cdots x^{(t)}_{(C)} ]$$$ be the matrix formed by concatenating the image column vectors of all coils from a single time. Let $$$X$$$ be the concatenation of all $$$X_{(c)}$$$ (or, equivalently, the concatenation of all $$$X^{(t)}$$$) for a single metabolite. The values of the pixels in the images for a metabolite are determined by solving the following optimization problem.
\begin{equation*}\text{minimize} \hspace{0.5em} (1/2)\|A\,X - b\|_2^2 + \sigma \sum_{c=1}^C \|X_{(c)}\|_\ast + \lambda \sum_{t=1}^{T} \|W\,X^{(t)}\|_{2,1},\end{equation*}
where $$$A$$$ is the linear transformation that represents the system, $$$W$$$ is the orthogonal Daubechies wavelet transform (applied to each image in the matrix $$$X^{(t)}$$$), $$$\|\cdot\|_\ast$$$ denotes the nuclear norm, $$$\|\cdot\|_{2,1}$$$ denotes the $$$L_{2,1}$$$ norm, and $$$\sigma\ge 0$$$ and $$$\lambda\geq 0$$$ are regularization parameters set by the user. We used the primal-dual hybrid gradient method to solve the above problem [10], which solves problems of the form
\begin{equation*} \underset{X}{\text{minimize}} \hspace{0.5em} F(X) + G( K \, X ).\end{equation*}
Let $$$I$$$ denote the identity matrix. By letting $$$F(X)=\lambda \sum_{t=1}^{T} \|W\,X^{(t)}\|_{2,1}$$$, $$$K = (A,I)$$$, and $$$G(Y_1,Y_2)=(1/2)\|Y_1-b\|_2^2 + \sigma \sum_{c=1}^C \|Y_2\|_\ast$$$, this problem is converted into the above form. After the individual images were created, they were combined using the square root of the sum-of-squares [3].

Results

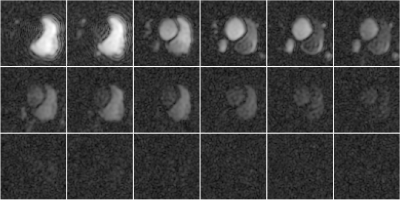
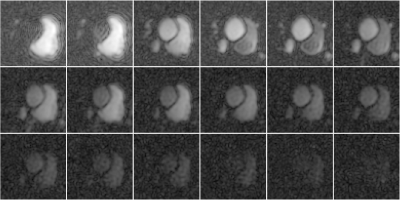
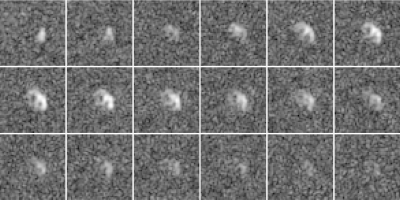
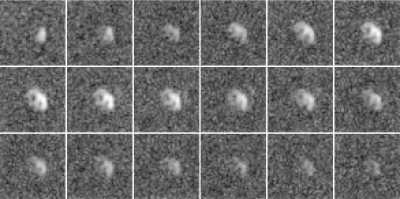
Figure 1 shows reconstructions of a slice of a heart after an injection of pyruvate separated by approximately $$$2$$$ seconds. Figure 2 shows the same reconstructions using the proposed algorithm. Note the improved quality of the images, especially from times starting at $$$24$$$ seconds.

Figure 3 shows reconstructions of lactate in a slice of a heart after an injection of pyruvate separated by approximately $$$2$$$ seconds. Figure 4 shows the same reconstructions using the proposed algorithm. Note the improved quality of the images, especially from times starting at $$$24$$$ seconds.

Conclusion

In this work, we present a model-based reconstruction algorithm that includes low-rank and joint-sparse regularization functions. We show that the result appears to retain more of the structure in the data even as the intensity values are dramatically diminished. In the future, we would like to combine images from multiple metabolites into a single reconstruction.