2623
Ultrafast Non-uniform Fast Fourier Transform for real-time radial acquisitions.1Medical Physics in Radiology, German Cancer Research Center (DKFZ), Heidelberg, Germany, 2Department of Physics and Astronomy, Heidelberg University, Heidelberg, Germany, 3Faculty of Medicine, Heidelberg University, Heidelberg, Germany
Synopsis
A GPU-based Fast non-Uniform Fast Fourier Transform (NUFFT) was implemented, which uses optimized libraries and algorithms such as stencils and managed memory to perform highly efficient transformations from the image to the k-space domain and vice-versa. In testing, the transform execution time was measured to be approximately 1ms for 32 channel data and a 256x256 grid size. A conjugate gradient based solution to the inverse NUFFT was also implemented, in which a solution was given within approximately 10ms. The proposed implementation has valuable applications for non-Cartesian real-time imaging.
Introduction
MR imaging using a radial k-space trajectory has advantageous properties for real-time imaging, such as motion robustness and inherent oversampling of the k-space center. However, reconstruction requires the employment of a non-Uniform Fast Fourier Transform (NUFFT), which is often the bottleneck in image reconstruction. As acquisitions are accelerated through sub-Nyquist k-space sampling, so the reconstruction becomes more computationally intensive through parallel imaging or compressed sensing, and the efficiency of the NUFFT becomes imperative for real-time imaging. Although advanced real-time radial reconstructions have been previously presented on the CPU1, GPU implementations of the NUFFT2-5 are more commonplace solutions to this problem.In this study, a new GPU-based implementation of the NUFFT, denoted as FNUFFT, is presented which uses modern C++ techniques and advanced parallel processing algorithms.
Theory and Methods
The NUFFT can be described as the following combination of linear operations applied to image vector $$$x$$$ and k-space vector $$$y$$$:$$ y = Ax = CFDx \text{ (forward)}$$
$$ x = A^H y = D^T F^H B^T y \text{ (adjoint)}$$
Where $$$D$$$ denotes deapodization, $$$B$$$ is the convolution onto a Cartesian grid and $$$F$$$ is the FFT operation. The adjoint transform is an approximation of the inverse NUFFT. The inverse solution can be found by iterative approaches. Each operation was implemented for parallelization on GPU architectures:
- FFT: The FFT was performed using the NVIDIA cuFFT library with optional stream splitting for multi-slice reconstruction.
- Convolution: The irregularly spaced data were sampled directly onto the Cartesian grid, with respect to overlaps in the center handled by atomics. Then the sampled data is distributed with the chosen window functor using a high-performance stencil. A stencil hereby represents a class of algorithms that update their elements in a multidimensional grid based on neighboring values based on a fixed pattern. The number of neighboring elements chosen to each side is denoted by the kernel width.
- Deapodization: The stencil writes out the weights distributed by the convolution kernel, which then yield the correction map through an iFFT of the convolution map.
- The inverse NUFFT was implemented using a conjugate gradient (CG) solver with total variation (TV) regularization6.
- Data transfer to and from the host to the device was handled using managed memory.
In-vivo image data were acquired on 7T MAGNETOM system (Siemens Healthineers, Germany), using a custom implementation of a 2D radial-FLASH sequence with a golden-angle increment7. Acquired data consisted of 256 lines and 256 samples per line in addition to 32 channels from the receiver coil.
The execution times of the adjoint FNUFFT were measured. Execution time included the execution instruction and runtime of the GPU kernels, but not disk I/O or memory allocations and was measured identically for all libraries. Adjoint times were measured for differing grid sizes and convolution kernel widths. Measurements were repeated 10 times. The execution time of the FNUFFT was compared to the CUNFFT library3, which was compiled and executed for the same PC hardware.
Results
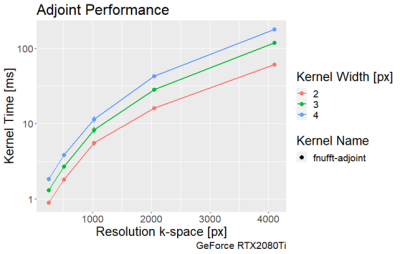
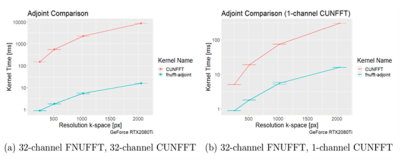
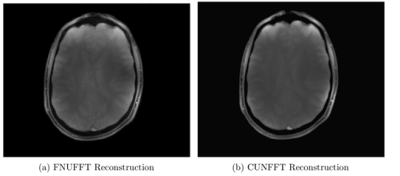
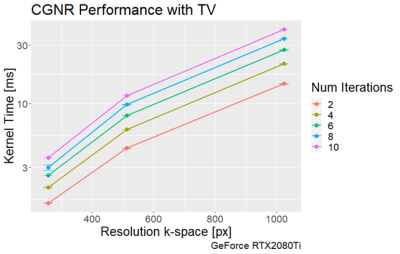
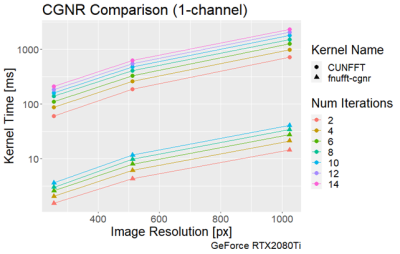
The execution times of the adjoint FNUFFT for different kernel widths and grid sizes are shown in Figure 1. It can be seen that execution times range from $$$(0.89 \pm 0.01)$$$ms for a grid size of 256x256 and kernel width of 2, up to $$$(61 \pm 0.6)$$$ms for a matrix size of 4000x4000 and kernel width of 4.From the comparison tests with the CUNFFT library (Figure 2), it was observed that the FNUFFT algorithm is faster in reconstructing 32 channels than the CUFFT reconstructs 1 channel while maintaining image quality, as shown in Figure 3. Figures 4-5 compare the performances of FNUFFT and CUNFFT for the inverse NUFFT with and without TV regularization.
Discussions and Conclusions
There are many approaches to implementing the NUFFT algorithm on GPU architectures, however the algorithms have either trajectory dependence, speed deficits, or accuracy loss. Applying highly optimized codes on modern CUDA architectures to form an NUFFT algorithm yields a combination that promises to solve the conflict of speed vs. accuracy while allowing the choice of the trajectory.Under certain conditions the FNUFFT exhibited a decrease in execution time compared to the CUNFFT by approximately 100. It should be noted however, that the CUNFFT is not optimized for multi-channel data. However even in the case of single channel data reconstruction for CUNFFT, a factor 10 decrease in execution time was observed. Further testing against other libraries is required to fully assess the performance of the FNUFFT.
The execution time of the FNUFFT allows for CG reconstructions with TV regularization on the order of 10ms, although there will be variations in the total number of iterations required for satisfactory image quality. The CG reconstruction could be further improved via use of the Toeplitz structure8, which would allow for the operator to be defined explicitly before the reconstruction.
Our proposed FNUFFT algorithm allows for sub-millisecond NUFFT operations using modern GPUs. This allows for iterative reconstructions and remove the NUFFT bottleneck in real-time MRI.
Acknowledgements
No acknowledgement found.References
[1] Uecker M et al. Nonlinear inverse reconstruction for real‐time MRI of the human heart using undersampled radial FLASH. Magn. Reson. Med 2010;63(6):1456-1462
[2] Sorensen TS et al. Accelerating the Nonequispaced Fast Fourier Transform on Commodity Graphics Hardware. IEEE-TMI 2008;27(4):538-547
[3] Kunis S and Kunis S. The nonequispaced FFT on graphics processing units. PAMM 2012;12(1):7-10
[4] Knoll F. et al. gpuNUFFT-An Open‐Source GPU Library for 3d Gridding with Direct Matlab Interface. Proc ISMRM 2014; Abstract 4297
[5] Smith et al. Trajectory optimized NUFFT: Faster non‐Cartesian MRI reconstruction through prior knowledge and parallel architectures. Magn. Reson. Med. 2019;81(3):2064-2071
[6] Block et. al. Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magn. Reson. Med. 2007;57(6):1086-1098
[7] Winklemann et al. An Optimal Radial Profile Order Based on the Golden Ratio for Time-Resolved MRI. IEEE Trans Med Imaging 2007;26(1):68-76
[8] Ou, Teresa. gNUFFTW: Auto-Tuning for High-Performance GPU-Accelerated Non-Uniform Fast Fourier Transforms. 2017 Technical Report # UCB/EECS-2017-90, University of California.
Figures