2622
Variational Feedback Network for Accelerated MRI Reconstruction1CIDSE, Arizona State University, Tempe, AZ, United States, 2RADIOLOGY, Mayo Clinic College of Medicine, Tempe, AZ, United States
Synopsis
Conventional Magnetic Resonance Imaging (MRI) is a prolonged procedure. Therefore, it’s beneficial to reduce scan time as it improves patient experience and reduces scanning cost. While many approaches have been proposed for obtaining high quality reconstruction images using under-sampled k-space data, deep learning has started to show promising results when compared with conventional methods. In this paper, we propose a Variational Feedback Network (VFN) for accelerated MRI reconstruction. Specifically, we extend the previously proposed variational network with recurrent neural network (RNN). Quantitative and qualitative evaluations demonstrate that our proposed model performs superiorly against other compared methods on MRI reconstruction.
Introduction
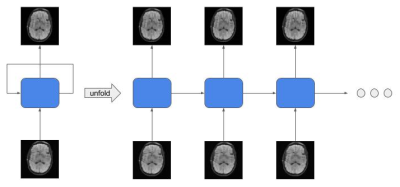
MRI is an important diagnostic tool for a lot of diseases. However, compared to other imaging techniques the scan time of MRI is relatively longer, which leads to poor patient experience and expensive cost. In order to improve the situation, it is meaningful to investigate if it is possible to decrease the scan time, while preserving the quality of the reconstructed images. Parallel Imaging (PI)[1, 2, 3], Compressed sensing (CS)[4], GRAPPA[3] are some important techniques. However, these algorithms have high complexity and take significant time to reconstruct the images, making them less practical. Recently, deep learning is providing promising results for many tasks in artificial intelligence[5, 6, 7, 8, 9, 10, 11, 12]. The superiority of deep learning based approach mainly comes from the nonlinearity capacity of the neural network[13, 14, 15]. In order to increase the complexity of the network, researchers usually increase the number of layers, which requires a lot of storage resources and also makes the model suffer from the overfitting problem. Recurrent structure is one of the solutions to the aforementioned problems. Its effectiveness has been shown in some recent studies[16, 17]. In this paper, we propose a Variational Feedback Network for accelerated MRI reconstruction, which is an extension to a previously proposed variational model[18] with feedback connections and recurrent structure(See Figure 1). We conduct comparisons among different models which demonstrate that our proposed model outperforms other leading neural networks for MRI reconstruction.Methods
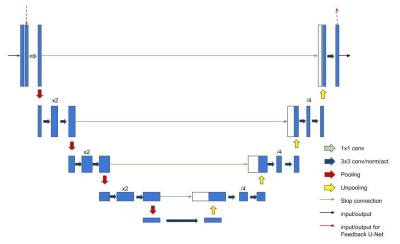
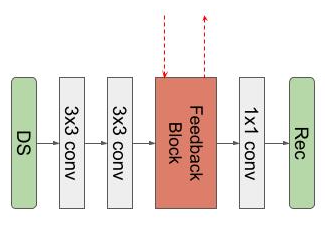
We propose our Variational Feedback Network (VFN) in this section.The basic block of our network is a U-Net[19]-like feedback network. We use it as part of the recurrent network, which is employed in the variational network.- Feedback Block:
- Feedback Network:
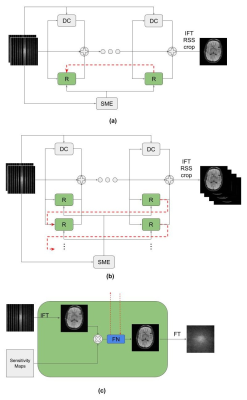
- Variational Network:
Results
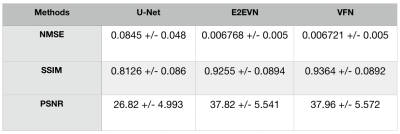
The multi coil brain datasets from fastMRI are used to evaluate our proposed VFN. Due to lack of ground truth, we used the validation data to evaluate the performance.We compare our VFN model with U-Net[19], E2EVN[18]. We train the networks for 25 epochs with batch size = 1. Adam optimizer[20] is used for with learning rate = 0.0001. The number of folds $$$T$$$ is set to 2. Table 1 shows the various metric evaluations.Conclusion
In this paper, we propose a new architecture - Variational Feedback Network for MRI reconstruction. The feedback connections and the recurrent U-Net structure can transmit the high level features back to the lower layers and refine the low level features, while reusing a lot of parameters.The experimental results have demonstrated that our proposed VFN outperforms other state-of-the-art methods.Acknowledgements
No acknowledgement found.References
[1] D. K. Sodickson and W. J. Manning, “Simultaneous acquisition of spatial harmonics (smash): fast imaging with radio frequency coil arrays,”Magnetic resonance in medicine, vol. 38, no. 4, pp. 591–603, 1997.
[2] K. P. Pruessmann, M. Weiger, M. B. Scheidegger, and P. Boesiger,“Sense: sensitivity encoding for fast mri,”Magnetic Resonance inMedicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, vol. 42, no. 5, pp. 952–962, 1999.
[3] M. A. Griswold, P. M. Jakob, R. M. Heidemann, M. Nittka, V. Jellus,J. Wang, B. Kiefer, and A. Haase, “Generalized autocalibrating partially parallel acquisitions (grappa),”Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance inMedicine, vol. 47, no. 6, pp. 1202–1210, 2002.
[4] D. L. Donoho, “Compressed sensing”, IEEE Transactions on information theory, vol. 52, no. 4, pp. 1289–1306, 2006.
[5] K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.
[6] G. Huang, Z. Liu, L. Van Der Maaten, and K. Q. Weinberger, “Densely connected convolutional networks,” in CVPR, vol. 1, no. 2, 2017, p. 3.
[7] P. L. K. Ding, B. Li, and K. Chang, “Convex dictionary learning for single image super-resolution,” in2017 IEEE International Conference on Image Processing (ICIP), Sep. 2017, pp. 4058–4062.
[8] J. Yang, Z. Wang, Z. Lin, S. Cohen, and T. Huang, “Coupled dictionary training for image super-resolution,” IEEE Transactions on Image Processing, vol. 21, no. 8, pp. 3467–3478, Aug 2012.
[9] A. Kumar, O. Irsoy, P. Ondruska, M. Iyyer, J. Bradbury, I. Gulrajani,V. Zhong, R. Paulus, and R. Socher, “Ask me anything: Dynamic memory networks for natural language processing,” in International conference on machine learning, 2016, pp. 1378–1387.
[10] A. Conneau, H. Schwenk, L. Barrault, and Y. Lecun, “Very deep convolutional networks for natural language processing,” arXiv preprint arXiv:1606.01781, vol. 2, 2016.
[11] C. Feichtenhofer, H. Fan, J. Malik, and K. He, “Slow fast networks for video recognition,” in Proceedings of the IEEE international conference on computer vision, 2019, pp. 6202–6211.
[12] C.-Y. Wu, C. Feichtenhofer, H. Fan, K. He, P. Krahenbuhl, and R. Gir-shick, “Long-term feature banks for detailed video understanding,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019, pp. 284–293.
[13] O. Delalleau and Y. Bengio, “Shallow vs. deep sum-product networks,” in Advances in Neural Information Processing Systems, 2011, pp. 666–674.
[14] R. Pascanu, G. Mont ́ufar, and Y. Bengio, “On the number of inference regions of deep feed forward networks with piece-wise linear activations,”CoRR, vol. abs/1312.6098, 2013. [Online]. Available:http://arxiv.org/abs/1312.6098
[15] G. F. Montufar, R. Pascanu, K. Cho, and Y. Bengio, “On the number of linear regions of deep neural networks,” in Advances in neural information processing systems, 2014, pp. 2924–2932.
[16] Q. Liao and T. Poggio, “Bridging the gaps between residual learning, recurrent neural networks and visual cortex,”arXiv preprint arXiv:1604.03640, 2016.
[17] J. Kim, J. Kwon Lee, and K. Mu Lee, “Deeply-recursive convolutional network for image super-resolution,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 1637–1645.
[18] Sriram, Anuroop, Jure Zbontar, Tullie Murrell, Aaron Defazio, C. Lawrence Zitnick, Nafissa Yakubova, Florian Knoll, and Patricia Johnson. "End-to-End Variational Networks for Accelerated MRI Reconstruction." arXiv preprint arXiv:2004.06688 (2020).
[19] O. Ronneberger, P. Fischer, and T. Brox, “U-net: Convolutional networks for biomedical image segmentation,” in International Conference on Medical image computing and computer-assisted intervention. Springer, 2015, pp. 234–241.
[20] D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,”arXiv preprint arXiv:1412.6980, 2014.
Figures