2620
Utilizing the Wavelet Transform's Structure in Compressed Sensing1Radiology and Biomedical Imaging, UCSF, San Francisco, CA, United States, 2Mathematics and Statistics, University of San Francisco, San Francisco, CA, United States, 3Robarts Research, Western University, London, ON, Canada, 4Biomedical Engineering, Northwestern University, Evanston, IL, United States, 5Electrical Engineering, Stanford University, Stanford, CA, United States, 6Radiology and Biomedical Imaging, University of California in San Francisco, San Francisco, CA, United States
Synopsis
In this work, we present a modification of the standard implementation of compressed sensing that takes advantage of the structure of the Daubechies wavelet transform. By doing so, we show that we retain additional detail in the reconstructed images when few data samples are used.
Introduction
Compressed sensing permits accurate reconstruction of MR images with fewer data samples than the number required to satisfy Nyquist's theorem [1]. To reconstruct the image with samples on a Cartesian grid, one solves the convex basis pursuit denoising (BPD) problem [2]:\begin{equation}
\underset{x\in\mathbb{C}^N}{\text{minimize}} \hspace{1em} \|\Psi x\|_1 \hspace{1em}
\text{subject to} \hspace{1em} (1/2)\| M\,F\,x - b \|_2^2 \leq \epsilon, \hspace{5em} (1)
\end{equation}
where $$$\Psi$$$ is a linear transformation, $$$F$$$ is the discrete Fourier transform, $$$M$$$ is the sampling mask, $$$b$$$ is a vector of the collected data, and $$$2\epsilon$$$ is a bound on the noise. This problem can be solved efficiently with standard algorithms (e.g. FISTA [3,4]).
Applications of compressed sensing rely on $$$\Psi$$$ operating as a sparsifying transform, a linear transformation that converts the image into a sparse or nearly sparse vector. Technically, if $$$A\,\Psi^{-1}$$$ satisfies the Mutual Coherence Conditions (MCC) [5], the Restricted Isometry Property (RIP) [6], RIP in levels (RIPL) [7,8], the Null Space Property (NSP) [9], or the Range Space Property (RSP) [10,11], then a solution of (1) is also an optimal point of the corresponding sparse signal recovery problem [2,12].
The Daubechies wavelet transform is often used as the sparsifying transform [13]. One might hope that the specific properties of the wavelet transform could be utilized to improve the quality of compressed sensing results. That is the subject of this work.
Methods
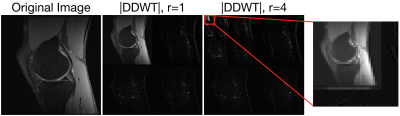
In this work, we identify an affine transformation that increases the sparsity of the transformed image when compared to the Daubechies wavelet transform of the same image. And we present a method to adapt this transformation into the existing compressed sensing framework.The Daubechies wavelet transform is comprised of two finite-impulse-response filters: a low-frequency filter and a high-frequency filter. Because natural images have high energy in the low frequencies, the corresponding elements of the wavelet transform will be not be sparse. An example of this is shown in Fig. 1. Note that the filters are not perfect and, therefore, result in aliasing. The wavelet transform is invertible because the two filters are perfect reconstruction filters.
Our approach is to use a fully-sampled center region to estimate the low-frequency bin of the wavelet transform. The size of the fully-sampled region satisfies the Nyquist theorem for the low-frequency image. The following optimization problem is solved to determine the remaining Fourier coefficients:
\begin{equation}\underset{y\in\mathbb{C}^N}{\text{minimize}} \hspace{0.5em} \| W \, ( y - F^\ast \,\hat{y}_L ) \|_1 \hspace{0.5em} \text{subject to} \hspace{0.5em} (1/2) \, \|M\,F\,y - b\|_2^2 < \epsilon, \label{eq:moreSparseImageRecon}\hspace{5em}(2)\end{equation}
where $$$\hat{y}_L=K_B\,M_L\,b$$$ is an estimate of the low-frequency bin of the wavelet transform. Above, $$$W$$$ is the Daubechies wavelet transform, $$$F^\ast$$$ is the adjoint of the unitary $$$F$$$, $$$K_B$$$ is a Kaiser-Bessel filter, and $$$M_L$$$ is a data sampling mask that isolates only the fully-sampled center region. We call (2) the More Sparse Basis Pursuit Denoising Problem (MSBPD).The sparsifying transform is now affine, rather than linear. But this problem can be converted into the basis pursuit denoising problem by defining $$$A=MFW^{-1}$$$ and $$$\beta=b - F^{\ast} \, \hat{y}_L$$$. The values of the wavelet coefficients with the low frequencies removed from the image can be recovered by solving
\begin{equation}\underset{z\in\mathbb{C}^N}{\text{minimize}} \hspace{0.5em} \| W \, z \|_1 \hspace{0.5em}\text{subject to} \hspace{0.5em} (1/2) \, \|A\,z - \beta\|_2^2.\hspace{5em}(3)\end{equation}
The key insight is that $$$z=W \, ( y - F^\ast \, \hat{y}_L )$$$ will be more sparse (have more values approximately equal to $$$0$$$) than $$$W\,y$$$. Thus, by the theorems of compressed sensing, the reconstructed image $$$y^{\star}=W^{-1}z^{\star} + F^\ast \hat{y}_L$$$ will be more accurate [1], where $$$z^{\star}$$$ is the solution to (3).
Results
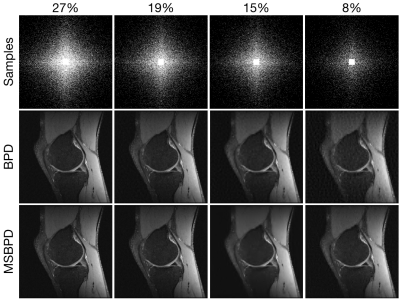
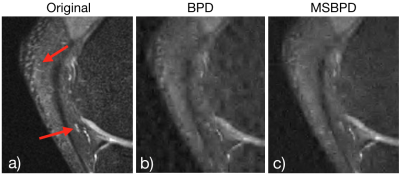
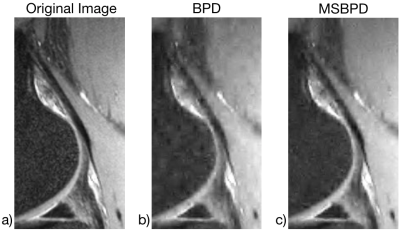
Figure 2 shows several variable density sampling patterns of different percentages and the results of solving the original BPD and the MSBPD problems. In all cases, MSBPD presents a more accurate image compared to the original image shown in Fig. 1. Fig. 3 zooms into a region of the kneecap when only $$$8\%$$$ of the data is sampled. The MSBPD reconstruction retains more of the fine detail than the BPD reconstruction. Fig. 4, which shows a zoomed in region of a different portion of the knee, shows a similar difference in quality.Conclusion
In this work, we present a modification of the standard implementation of compressed sensing that takes advantage of the structure of the Daubechies wavelet transform. By doing so, we show that we retain additional detail in the reconstructed images when few data samples are used.Acknowledgements
No acknowledgement found.References
[1] Emmanuel J Cand`es and Michael B Wakin. An introduction to compressive sampling [a sensing/sampling paradigm that goes against the common knowledge in data acquisition]. IEEE signal processing magazine, 25(2):21–30, 2008.
[2] Scott Shaobing Chen, David L Donoho, and Michael A Saunders. Atomic decomposition by basis pursuit.SIAM review, 43(1):129–159, 2001.
[3] Amir Beck and Marc Teboulle. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM journal on imaging sciences, 2(1):183–202, 2009.
[4] Katya Scheinberg, Donald Goldfarb, and Xi Bai. Fast first-order methods for composite convex optimization with backtracking.Foundations of Computational Mathematics, 14(3):389–417, 2014.
[5] David L Donoho and Michael Elad. Optimally sparse representation in general (nonorthogonal) dictionaries via L1 minimization. Proceedings of the National Academy of Sciences, 100(5):2197–2202,2003.
[6] Emmanuel J Cand`es. The restricted isometry property and its implications for compressed sensing. Comptes rendus mathematique, 346(9-10):589–592, 2008.
[7] Ben Adcock, Anders C Hansen, Clarice Poon, and Bogdan Roman. Breaking the coherence barrier: A new theory for compressed sensing. In Forum of Mathematics, Sigma, volume 5. Cambridge UniversityPress, 2017.
[8] A Bastounis, B Adcock, and AC Hansen. From global to local: Getting more from compressed sensing. SIAM News, 2017.
[9] Albert Cohen, Wolfgang Dahmen, and Ronald DeVore. Compressed sensing and best k-term approximation. Journal of the American mathematical society, 22(1):211–231, 2009.
[10] Yun-Bin Zhao. RSP-based analysis for sparsest and least L1-norm solutions to underdetermined linear systems. IEEE Transactions on Signal Processing, 61(22):5777–5788, 2013.
[11] Yun-Bin Zhao. New and improved conditions for uniqueness of sparsest solutions of underdetermined linear systems. Applied Mathematics and Computation, 224:58–73, 2013.
[12] Shaobing Chen and David Donoho. Basis pursuit. InProceedings of 1994 28th Asilomar Conference onSignals, Systems and Computers, volume 1, pages 41–44. IEEE, 1994.
[13] Michael Lustig, David Donoho, and John M Pauly. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 58(6):1182–1195, 2007.
Figures