INTRODUCTION

T1 and T2-weighted (T1w, T2w) imaging, typically performed using fast spin-echo (FSE)-based methods, are widely used for clinical MR examinations. Despite recent progress of fast imaging technique(1)(2), there is still a need to shorten scan times. In addition, FSE-based methods are generally limited to 2D acquisitions for most clinical applications.
Recently, a T2 mapping method using RF phase modulated gradient echo (GRE) imaging, with small RF phase increments, was proposed(3). In this previous work, we demonstrated the ability to encode T2 information into the GRE signal phase.
In the current work, we now propose a novel method for simultaneous T1w and T2w imaging, which is achieved by encoding contrast information into the real and imaginary components of a signal, using GRE imaging with RF phase modulation.

THEORY

In this work, we use Sobol's approach to explain the steady-state characteristics of the RF phase-modulated GRE signal(4). The RF phase modulation was performed by incrementing the transmit RF phase ($$$\phi$$$) quadratically such that $$$\phi (n) = \phi (n-1) + n \theta$$$, where $$$theta$$$ is the RF phase increment. The signal with RF pulse with flip angle (FA) of α, RF phase of $$$\phi$$$, and a repetition time of TR can be expressed as
$$Re(S) = \beta \eta e^{-\frac{TR}{T2}}$$
$$Im(S) = \beta [\eta^2 - \epsilon (e^{-\frac{TR}{T2}}-\epsilon)]$$
with
$$\beta = \frac{ (1-e^{-\frac{TR}{T1}}) M_0 sin \alpha}{ (e^{-\frac{TR}{T2}} - \epsilon) [ e^{-\frac{TR}{T2}} (cos \alpha - e^{-\frac{TR}{T1}}) + \epsilon (1 - e^{-\frac{TR}{T1}} cos \alpha) ] - \eta^2 (1 - e^{-\frac{TR}{T1}} cos \alpha) }$$
where M₀ is the proton density, and $$$\epsilon$$$ and $$$\eta$$$ are real coefficients, determined by recursive calculation depending on T1, T2, TR, α, and θ (4). The contrast of the GRE is sensitive to θ while it also depends on TR and α.
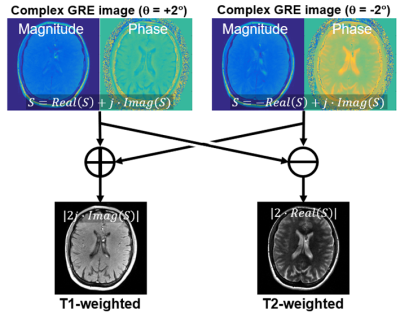
In general, the acquired signal includes a background phase. Two-pass imaging was adopted to remove this, achieved by using acquisitions with positive and negative polarities of RF phase increments, as explained in Fig. 1.
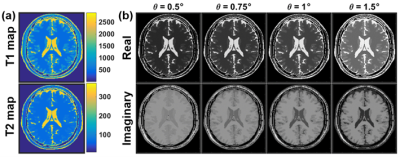
To show the contrast dependency on θ, a simulation study was performed using a numerical brain phantom, downloaded from the MRiLab project(5). The GRE signal of the brain phantom was calculated using Eq. 1 and 2 with of 0.5, 0.75, 1.0, and 1.5°.
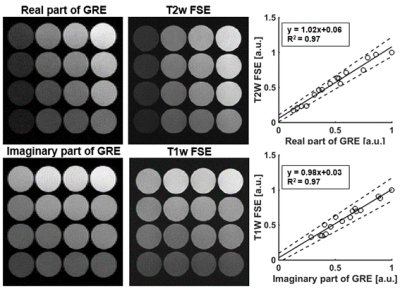
A phantom consisting of 16 vials with different T1 and T2 values was imaged using the proposed method. Conventional T1w and T2w FSE images were also obtained as references. The intensity of the acquired signal was measured and compared between the proposed method and FSE. The intensities were normalized using the maximum intensity of the images.
We evaluated the feasibility of simultaneous T1w and T2w imaging of the brain comparing the proposed method with FSE. Healthy volunteers were recruited from an Institutional Review Board (IRB) approved database of healthy volunteers.

RESULTS

As shown in Figure 2, simulations demonstrated that T1w and T2w contrast can be encoded into the GRE signal's real and imaginary components. Figure 2a shows quantitative T1 and T2 maps of the numerical phantom used in this study. Figure 2b demonstrates that that T1 weighting increases as θ decreases while stronger T2 weighting can be obtained as θ increases.
Figure 3 shows T1w and T2w images of the phantom acquired using the proposed method and with FSE. The signal intensities of the real and imaginary components of the proposed method agreed well with T2w (R² = 0.97) and T1w (R² = 0.97) FSE signals as shown in the plot in Figure 3.
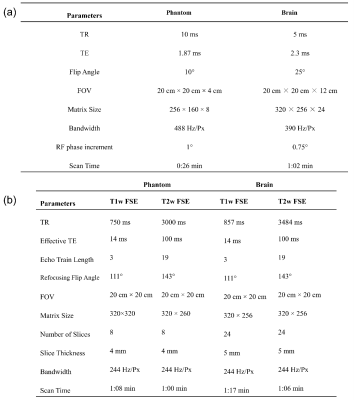
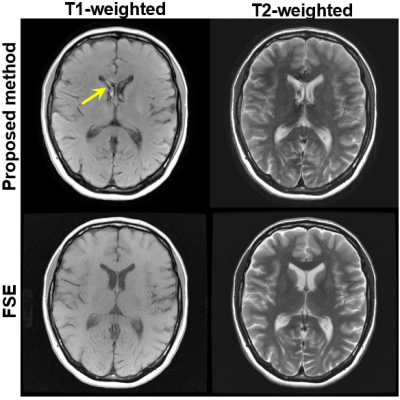
Example images of the brain using the proposed method compared with FSE imaging are shown in Figure 4. Typical T1w and T2w contrasts of the brain were observed using the proposed method, although there is a slight mismatch of the contrast of gray-white matter in the proposed method compared to FSE imaging. Also, possible motion-induced artifacts were seen in the CSF (arrow). Acquisition for the proposed method was 1:02 min, while FSE imaging for T1w and T2w required a total of 2:23 min. Imaging parameters for phantom and volunteer experiments are shown in Tab. 1.

DISCUSSION

In this work, we have proposed and demonstrated the feasibility of a novel RF phase modulated 3D GRE imaging method to obtain simultaneous T1w and T2w images. Our results demonstrated that the proposed method enables fast acquisition with T1w and T2w contrast compared to conventional FSE imaging.
The proposed method could be used as an alternative to conventional T1w and T2w imaging. Several imaging techniques using GRE imaging with a small RF phase increment have been proposed to obtain various contrast mechanisms(6) and quantitative maps(7), which utilize the magnitude of the acquired signal. On the other hand, the proposed method provides T1w and T2w contrasts from the real and imaginary components simultaneously, resulting in reducing scan time.
There are limitations of the proposed method. Fat suppression was not included in this study. It should be straightforward to combine chemical shift encoded water-fat separation strategies to facilitate fat suppression. Other potential limitations such as motion and short T2* should be investigated for clinical use.

CONCLUSION

We successfully developed and demonstrated the feasibility of a novel RF phase modulated 3D GRE imaging method for rapid simultaneous T1w and T2w imaging.

Acknowledgements

We wish to acknowledge support from the UW-Madison Department of Radiology, UW Institute for Clinical and Translational Research, and the Clinical and Translational Science Award of the NCATS/NIH. Further, we wish to acknowledge GE Healthcare who provides research support to the University of Wisconsin. Finally, Dr. Reeder is a Romnes Faculty Fellow, and has received an award provided by the University of Wisconsin-Madison Office of the Vice Chancellor for Research and Graduate Education with funding from the Wisconsin Alumni Research Foundation.