2613
Faster and better HARDI using FSE and holistic reconstruction1Radiology, Universitair Ziekenhuis Brussel, Brussels, Belgium, 2Department of Computer Science, Technical University of Munich, Garching, Germany, 3Imec-Vision Lab, University of Antwerp, Wilrijk, Belgium, 4Bio-Imaging Lab, University of Antwerp, Wilrijk, Belgium
Synopsis
To accelerate the acquisition of HARDI data, compressed sensing can be used to subsample the data both in k-space and in q-space, using a holistic algorithm for the combined reconstruction. Fast spin echo (FSE) data has fewer deformation artefacts as EPI data, but often requires a multishot acquisition, making subsampling k-space more attractive. In this work FSE data was subsampled retrospectively to investigate different types of subsampling: subsampling q-space only, also using 1D k-space subsampling, or using q-space and alternated 1D k-space subsampling. The results show that for a given subsampling factor the alternated 1D k-space subsampling strategy performs best.
Introduction
Diffusion models beyond DTI require more volumes to be acquired, and their long acquisition time makes them difficult to apply in clinical and research contexts. Compressed sensing (CS) can alleviate this problem by enabling us to reconstruct a full signal from partial k-space or q-space acquisitions. A combined k-q-space reconstruction might prove beneficial over subsampling in only q-space or over k-space and subsequent q-space reconstruction, but this has not yet been proposed for HARDI. While the above is generally true, CS can be of particular value in a preclinical small-animal imaging context, where the scale of the hardware limits the use of parallel MRI and multislice imaging. In this research, several subsampling strategies are tested in a simulation experiment on preclinical FSE-HARDI data of a mouse brain. FSE is particularly suitable for combined k-q-space subsampling due to the necessity for multi-shot acquisitions and the reduced deformation artefacts.Methods
In vivo mouse brain data acquired using a FSE diffusion sequence on a 7T Pharmascan scanner (Bruker, Ettlingen, Germany) was used. Details of the acquisition can be found in 1. The fully sampled diffusion data, consisting of 60 directions (b = 2500 s/mm2) and b0 images, was denoised 2,3 and preprocessed using FSL 4. Starting from this data, subsampled multicoil acquisitions were simulated and simultaneous k-q-space reconstruction was performed using the holistic image reconstruction technique proposed by Golkov et al 5.This technique reconstructs the entire 6D image jointly while using regularization terms along 3D image space for each q-space coordinate, on each q-space shell of each voxel, and on the corresponding ODF of each voxel. This allows different 6D image coordinates to share information (thus filling the subsampled “knowledge gaps” and reducing noise) and to be optimized jointly for improved image quality. The resulting nonconvex optimization problem is solved by adapting the primal-dual hybrid gradient method 6 to nonlinear operators 7,5.
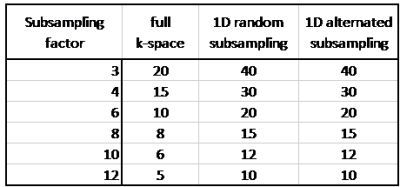
Three different strategies were used for the subsampling: 1) ‘full k-space’: subsampling only in q-space; 2) ‘1D random subsampling’: acquiring half of k-space using random subsampling in the phase-encoding direction (rostral-caudal), with a power law as sampling probability function 1; 3) ’1D alternated subsampling’: acquiring only half of k-space by regular subsampling, with the subsampling direction being rostral-caudal for half of the volumes and left-right for the other half. Six different subsampling factors R∈{3,4,6,8,10,12} were tested. Subsampling factors and number of diffusion volumes used are listed in Table 1. The difference between reconstructed and original data was evaluated by calculating the root-mean-squared deviation (RMSD) of image intensity over all volumes.
Results
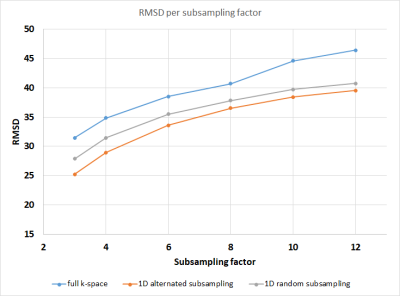
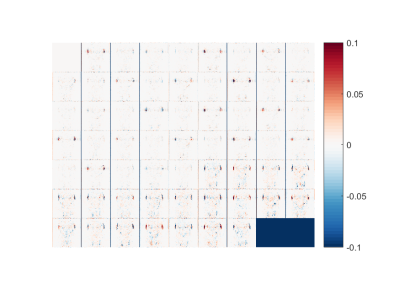
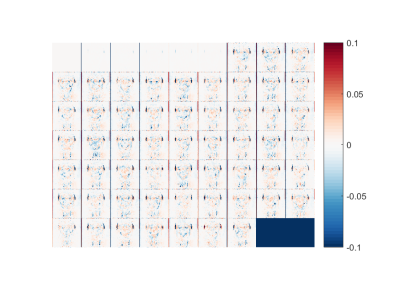
Figure 1 shows the RMSD values for all experiments. As expected, higher subsampling factors have larger errors. Using only subsampling in q-space results in greater errors than combined k- and q-space subsampling, while subsampling k-space in two directions gives the best results. Figures 2-3 show the error maps for the best case (R=3, using 1D alternated subsampling) and worst case (R=12, using full k-space) scenarios, respectively. It can be seen that the largest errors occur outside of the brain near the ears. In the brain, the error is smaller than 5%.Discussion
The results clearly indicate that subsampling both k- and q-space can result in improved reconstructions. This effect is enhanced when subsampling is applied in two dimensions in k-space. The FSE acquisition used in these experiments is well suited for such a subsampling approach, as switching the phase-encoding direction will not result in vastly different deformation artefacts as it does when using an EPI acquisition, which might hinder the reconstruction. These simulation experiments provide a proof of principle, which should be expanded by data actually acquired using such a scheme. The holistic algorithm which is used here can be expanded to include motion and eddy current correction (estimated via preliminary standard reconstruction) in the operator, resulting in an almost single step reconstruction. Nonetheless, correcting strong distortions is in general worse than not having them in the first place, by using FSE.Conclusion
Simultaneous subsampling of k- and q-space of HARDI data can improve the reconstruction quality over only q-space subsampling for a given subsampling factor, when the reconstruction is done in a single step. Alternating the phase-encoding direction for each volume improves the results even further. Successful reconstructions can be acquired with as little as 10 q-space coordinates and half of the k-space, which also translates in half the acquisition time for a multi-shot FSE or EPI acquisition.Acknowledgements
This work was supported by the interdisciplinary PhD grant (ID) UA BOF-DOCPRO 2012, the EU’s Seventh Framework Programme (grant FP7/2007-2013; INMiND) [grant agreement 278850], the molecular Imaging of Brain Pathophysiology (BRAINPATH) [grant FP7-PEOPLE-2013-IAPP-612360], by the Hercules stichting [grant agreement no. AUHA/012], HFSP RGP0006/201.References
1. Naeyaert, M. et al. Accelerating in vivo fast spin echo high angular resolution diffusion imaging with an isotropic resolution in mice through compressed sensing. Magn. Reson. Med. 85, 1397–1413 (2021).
2. Veraart, J. et al. Denoising of diffusion MRI using random matrix theory. Neuroimage 142, 394–406 (2016).
3. Veraart, J., Fieremans, E. & Novikov, D. S. Diffusion MRI noise mapping using random matrix theory. Magn. Reson. Med. 76, 1582–1593 (2016).
4. Jenkinson, M., Beckmann, C. F., Behrens, T. E. J., Woolrich, M. W. & Smith, S. M. FSL. Neuroimage 62, 782–790 (2012).
5. Golkov, V., Portegies, J. M., Golkov, A., Duits, R. & Cremers, D. Holistic Image Reconstruction for Diffusion MRI. in Computational Diffusion MRI. Mathematics and Visualization. (eds. Fuster, A., Ghosh, A., Kaden, E., Rathi, Y. & Reisert, M.) 27–39 (Springer, Cham., 2016). doi:10.1007/978-3-319-28588-7_3
6. Pock, T., Cremers, D., Bischof, H., Chambolle, A.: An algorithm for minimizing the Mumford-Shah functional. In: 2009 IEEE 12th International Conference on Computer Vision (ICCV). Number 813396, IEEE, pp. 1133–1140 (2009).
7. Valkonen, T.: A primal-dual hybrid gradient method for non-linear operators with applications to MRI. Inverse Prob. 30(5), 055012 (2014).
Figures