Introduction

MR parametric mapping is a powerful tool for tissue characterization [1-3]. The most common way to get it is to acquire multi-weighted images along a parametric dimension with different pulse sequence parameters, which significantly lengthens the scan time and hinders its widespread clinical application [4,5]. Then, many researches devote themselves to research on shortening the scan time. At present, based on compressed sensing (CS), the mainstream method is to reconstruct the weighted images and parametric maps in an interactive way. However, this multi-objective reconstruction often forms a highly nonconvex optimization which is NP-hard to solve in general [6]. In addition to CS, interpolation for undersampled k-space data is another effective way to realize fast imaging. What’s more, this method often converts some precise requirements (coil sensitivity) to implicit constraints, thus reducing the model complexity [7-9]. Inspired by this, in this work, we proposed a k-space interpolation method for fast parametric mapping which implicitly absorbs the exponential decay about parameter map as an annihilation relation and reduce it to a convex constraint. Algorithmically, we can solve this problem using alternating directional minimization (ADM) method. To further improve efficiency, we generalize the ADM algorithm in an unrolling manner. The experimental results on in-vivo datasets show that the proposed based method achieves superior reconstruction and mapping performance.

Theory and method

Let $$$U=[u_1,\ldots,u_{Nt}]\in \mathbb{C}^{d^{Nt\times Nc}}$$$, where $$$u_i=[u_{i,1},\ldots,u_{i,Nc}]\in\mathbb{C}^{d^{Nc}}$$$ denotes the $$$i$$$-th weighted multichannel image. $$$B=[b_1,\ldots,b_Nt]\in\mathbb{C}^{d^{Nt\times Nc}}$$$ denotes the undersampled k-space measurement and $$$\widehat{U}=[\widehat{u_1},\ldots,\widehat{u_{Nt}}]$$$ denotes the Fourier transform of $$$U$$$. Tacking $$$T_{1\rho}$$$ mapping as an example, the weighted images along spin-lock time (TSL) follow an exponential decay, i.e.,$$u_{i,j}=u_{0,j}e^{-\frac{TSL_{i}}{T_{1\rho}}}, \forall i=1,\ldots,Nt,j=1,\ldots,Nc.$$Naturally, if the decayed images could be compensated to the same intensity level as the first TSL image, the rank of the spatial-TSL matrix would be one, i.e., $$\text{rank}\left(\left[u_{1,j}e^{-\frac{TSL_{1}}{T_{1\rho}}},\ldots,u_{Nt,j}e^{-\frac{TSL_{Nt}}{T_{1\rho}}}\right]\right), \forall j=1,\ldots,Nc ~~~(1) $$ which acts as a basic constraint in SCOPE method [10,11]. Unfortunately, for the above highly nonconvex nonsmooth constraint, it is NP-hard to find optimal solutions $$$u_{i,j}$$$ and $$$T_{1\rho}$$$. Then, we propose to convert the signal compensation to an implicit manner. Let $$$c_i$$$ denote the $$$i$$$-th coil-sensitivity and $$$\alpha_i=e^{\frac{TSL_{i}}{T_{1\rho}}}$$$. Since $$$c_ku_{0,j}=c_ju_{0,k}$$$, it holds$$\alpha_ic_ku_{i,j}=\alpha_sc_ju_{s,k}\Leftrightarrow \widehat{\alpha_i} * \widehat{c_k} *\widehat{u_{i,j}}=\widehat{\alpha_s} * \widehat{c_j} *\widehat{u_{s,k}}$$which can be compactly represented as:
$$[\textbf{H}(\widehat{u_{i,j}}),\textbf{H}(\widehat{u_{s,k}})]\left[\begin{aligned}\widehat{c_k}*\widehat{\alpha_i}\\-\widehat{c_j}*\widehat{\alpha_s}\end{aligned}\right]$$
where $$$\textbf{H}(\widehat{u_{i,j}})$$$ represents the Hankel-structured matrix for linear convolution. With above derivation, signal compensation (1) can be implicitly absorbed into the following annihilation relation $$\mathcal{H}(\widehat{U})h=0~~~(2)$$where$$ \mathcal{H}(\widehat{U}):=[\textbf{H}(\widehat{u_{1,1}}),\ldots,\textbf{H}(\widehat{u_{1,Nc}})|\ldots|\textbf{H}(\widehat{u_{Nt,1}}),\ldots,\textbf{H}(\widehat{u_{Nt,Nc}})]$$
Based on constraint (2), the corresponding Lagrangian form of k-space interpolation problem can be depicted as following convex optimization: $$ \min_{\widehat{U}\in \mathbb{C}^{d^{Nt\times Nc}}}\frac{1}{2}\|\mathcal{M}(\widehat{U})-B\|^2+\lambda\|\mathcal{H}(\widehat{U})h\|^2$$
where $$$\mathcal{M}$$$ denotes the mask, and $$$h$$$ can be estimated from calibration data. Considering the noise interference and structure similarity among weighted images, we further adopt joint TV regularization $$$\mathcal{R}(\nabla U)=\sum_{j=1}^{Nc}\left\|\left(\sum_{i=1}^Nt\|\nabla u_{i,j}\|^2\right)^{1/2}\right\|_1$$$. Introducing auxiliary variables $$$Q=\mathcal{H}(\widehat{U}),V=\nabla U$$$, the corresponding penalty function can be formulated as $$ L(\widehat{U},Q,V)=\frac{1}{2}\|\mathcal{M}(U)-B\|^2+\lambda\|Qh\|^2+\frac{\rho}{2}\|\mathcal{H}(\widehat{U})-Q\|^2+\mu\mathcal{R}(V)+\frac{\beta}{2}\|\nabla U-V\|^2.~~~(3)$$ The ADM for solving it reads:
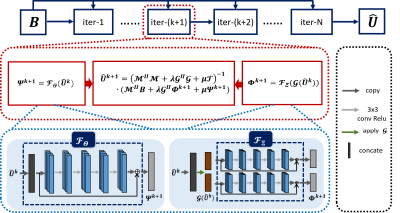
$$\left\{\begin{aligned}\widehat{U}^{k+1}=&\arg\min_{\widehat{U}}L(\widehat{U},Q^k,V^k)\\Q^{k+1}=&\arg\min_{Q}L(\widehat{U}^{k+1},Q,V^k)\\V^{k+1}=&\arg\min_{V}L(\widehat{U}^{k+1},Q^{k+1},V)\\\end{aligned}\right.$$Particularly, detailed iterative scheme of above algorithm is depicted in Figure 1. In Algorithm 1, the filter $$$h$$$ estimation usually requires decomposition of the matrix $$$\mathcal{H}(\widehat{U})$$$, which is computationally time-consuming. Now, we attempt to estimate the annihilation process about $$$h$$$ using CNN. For the subproblem $$$Q^{k+1}$$$ in Figure 1, if , we have$$Q^{k+1}=\rho \mathcal{H}(\widehat{U^k})\cdot(\lambda hh^{H}+\rho\mathcal{I})^{-1}\approx\mathcal{H}(\widehat{U^k})\left(\mathcal{I}-\frac{\lambda}{\rho}hh^{H}\right).$$Through the thought of unrolling [12], we use residual network block to replace the projection operator $$$\left(\mathcal{I}-\frac{\lambda}{\rho}hh^{H}\right)$$$ and also use residual network block to generalize joint TV. Then, we derive a CNN-based k-space interpolation method, the framework of which is depicted in Figure 2.

Experiment

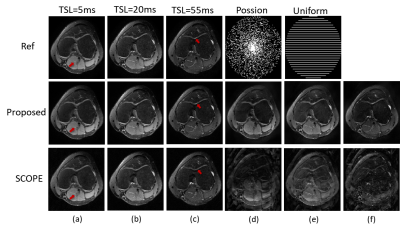
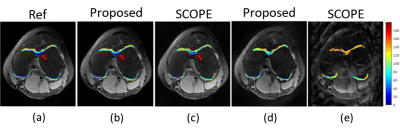
The proposed k-space interpolation network was compared with SCOPE method on $$$T_{1\rho}$$$ parameter mapping for knee cartilage. The $$$T_{1\rho}$$$-weighted knee MR dataset were acquired with a 3D extended echo train (MATRIX) sequence on a 3T scanner. The dataset is a multi-slice 3D dataset consisting of 12-channel slices from 7 subjects. Six of them were used for training and the remaining one for testing. The undersampled data with real and imaginary parts are concatenated from all the 5 TSLs together as Input. Each convolution layer consists of 192 3 x 3 filters followed by ReLU activated function for residual network blocks $$$ \mathcal{F}_{\Xi}, \mathcal{F}_{\Theta}$$$. The iteration number is set as N=10 and unrolled network is trained via 100 epochs with Adam optimizer at a learning rate . To verify the superiority of our proposed method, we compared it with SCOPE in terms of the accuracy of weighted image reconstruction and $$$T_{1\rho}$$$ parameter map estimation. For these two aspects, Figure 3 and 4 show our superior performances respectively.

Conclusion

This work proposed a generalized physical decayed annihilation-based k-space interpolation method for fast parameter mapping. Preliminary experiments demonstrated its effectiveness.