Introduction

Improvement in spatial-temporal-resolution and phase variation representation directly benefits the sensitivity and specificity of dynamic phase mapping, for various applications such as MRI guided focused ultrasound (MRIgFUS) surgery, in which MRI phase mapping can be used for temperature monitoring and verifying targeting and heating for thermal ablation. However, it is challenging to simultaneously achieve high signal quality, accurate phase-represented-temperature-variation and high spatial-temporal-resolution due to trade-offs that exist among resolution, acquisition time and signal-to-noise ratio (SNR). One approach to resolve this challenge is to use super-resolution¹ to reconstruct high resolution images using spatially sub-voxel-shifted (along the slice-selection direction) low resolution images^{2, 3}. As shown in recent publications, high spatial-temporal-resolution MRI could be achieved when combining super-resolution and multi-band (e.g., SLIDER-SMS^{4, 5}). However, acceptable phase variation reconstruction and reduction in susceptibility signal loss in dynamic MRI temperature mapping data obtained with thick slices has not been well achieved with existing magnitude-only super-resolution reconstruction scheme. In this project, we proposed and developed complex-valued multi-band super-resolution reconstruction method to compensate these deficiencies.

Methods

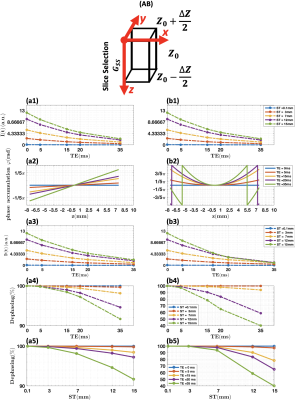
I). Simulation of through-plane susceptibility effect.
A simplified simulation of the effects of local through-plane susceptibility gradients on signal intensity was done in a single voxel to evaluate the slice thicknesses in which super-resolution reconstruction would be most effective. Image intensity loss due to spin dephasing caused by susceptibility gradients in the slice-selection direction $$$(G_{ss})$$$ can be represented by^{6, 7}:$$I=I_{0}\cdot e^{\frac{-t}{T_{2}}}\cdot [\sum_{z=z_{0}-\frac{\triangle z}{2}}^{z_{0}+\frac{\triangle z}{2}}(P(z)\cdot e^{i\phi(z)})]\cdot(dz)\;\;\;\;\;\;\;(1)$$ In which: $$$I_{0}$$$ is the initial image intensity without T2* decay and susceptibility gradients; $$$z_{0}$$$ is the center location of the voxel; $$$\triangle z$$$ is the slice thickness; $$$P(z)$$$ is a pseudo-rect slice profile; $$$\phi(z)$$$ is the phase accumulation due to the susceptibility gradient and given by $$$\phi(z)=\gamma\cdot G_{ss}\cdot TE\cdot z$$$. The dephasing signal loss is $$$\frac{I}{I_{0}}$$$.

II). Simulation of spatial-temporal super-resolution with multi-band (R=2) technique for local region-of-interest (ROI) temperature mapping.
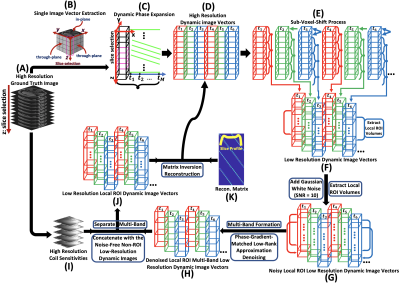
High-resolution 3D static complex-valued image volume was acquired on $$$Siemens 3T$$$ scanner as ground truth. An artificially generated linear signal with slope of $$$-0.77\frac{\triangle\phi}{\triangle T}$$$ (total 60 time points) was applied to the phase of each of the voxels within a chosen ROI. The slope is in the unit of $$$\frac{\triangle\phi}{\triangle T}$$$, meaning that how much the phase changes per unit temperature. The slope is expressed as^{8, 9}: $$slope=\frac{\triangle\phi}{\triangle T}=360\times \alpha\times\gamma\times B_{0}\times TE\;\;\;\;\;\;\;(2)$$ In which: $$$\alpha=-0.01\frac{ppm}{^{\circ}C}$$$ is water chemical shift. The rest of the non-target voxels were repeated 60 times without variation in phase. After the temporal phase expansion, every 3 slices were then weighted by their corresponding slice profile portions and summed to form the low-resolution image volume at each time point with the corresponding number of sub-voxel-shifts. Gaussian white noise (SNR = 10) was then added, and a local 3D ROI was extracted. Dynamic multi-band-low-resolution images were finally created by combining the first and the second half of corresponding low-resolution image volumes along the slice-selection direction. Phase-gradient-matched low-rank approximation denoising procedure¹⁰ was developed and applied to the local dynamic multi-band-low-resolution images. High-resolution coil sensitivities were then used to separate the multi-band. The images of non-ROI regions from the noise-free sub-voxel-shifted low-resolution images were concatenated with the denoised local ROI dynamic low-resolution images for the reconstruction. The reconstruction matrix was created using the slice profile array. The final reconstruction was done through matrix inversion using complex-valued images. Fig. 1 shows the general workflow.

Results

I). Simulation on susceptibility effect.
As shown in Fig. 2, significant dephasing effects can be observed when the acquisition slice thickness increases in both linear (Fig. 2. (a5)) and nonlinear susceptibility gradient (Fig. 2. (b5)) cases, which indicates the feasibility that susceptibility artifact can be effectively reduced by decreasing the slice thickness using super-resolution reconstruction with thick slice acquisition.

II). Simulation on local ROI temperature mapping.
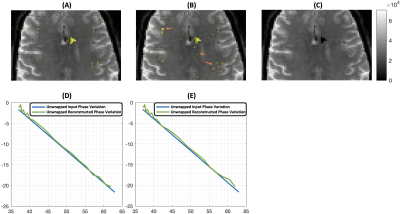
The first row of Fig. 3 shows the reconstructed ROI heat maps overlapped on ground truth image with (A) and without (B) the denoising procedure, respectively, and the ROI location on the ground truth image (C). Comparing to (B), (A) is cleaner with less hot voxels outside of ROI (indicated by arrows in (B)) due to noise. As indicated in (D) and (E), the linear phase variation was successfully reconstructed using complex-valued super-resolution. The phase-gradient-matched low-rank approximation denoising did improve the reconstruction accuracy (D) when compared with the one that did not apply the denoising procedure (E).

Discussion

Results have shown that the proposed reconstruction method can effectively recover signal loss caused by susceptibility artifacts and can generate accurate dynamic phase variation. Phase information can be utilized in reconstruction to significantly reduce the susceptibility artifact, benefiting applications relying on phase mapping (e.g., MRIgFUS). Our proposed method can be integrated with multi-band to further improve scan efficiency.

Acknowledgements

No acknowledgement found.