Introduction

Recently a T₁W enhanced contrast (T₁WE) method was proposed in the context of multi-contrast imaging^1,2. By scanning a 3D GRE sequence with two flip angles (e.g. 6° and 24°), both PDW and T₁W images can be obtained. And by defining a T₁WE signal as the signal difference between these T₁W and PDW signals, T₁ contrast can be enhanced^1,2. However, spatial inhomogeneity in both transmitting (B_1t) and receiving (B_1r) RF fields are still in effect after subtraction, affecting the uniformity of resultant images. The T₁WE images are calculated based on coil-combined images, with both the subtraction and coil-combination (e.g. sum-of-square) leading to compromise in SNR. Last but not the least, signal subtraction can lead to erroneous image contrast depending on the choice of flip angles.
In this work, we propose an augmented T₁W (aT₁W) technique to achieve computationally enhanced T₁ contrast while addressing all the above issues of T₁WE. By using division instead of subtraction, as well as incorporating the multi-dimensional integration (MDI) method³, the aT₁W images offers improved and robust T₁ contrast, as well as superior image SNR over arbitrary scanning parameters.

Methods

The ISS signal of a GRE sequence is⁴:
$$S(\alpha)=C\frac{(1-E_{1})\sin(\alpha)}{1-E_{1}\cos(\alpha)}e^{-TE/T_2^*} [1]$$
Where α is the flip angle, C the coil sensitivity, TE/TR the echo/repetition times, and $$$E_{1}=e^{-TR/T_1}$$$. For simplicity, the baseline signal is assumed to be 1 and ignored. We define the aT1W signal as:
$$S_{aT1W}\equiv\frac{S(\alpha_{2})}{S(\alpha_{1})}=\frac{sin(\alpha_{2})}{sin(\alpha_{1})}\bullet\frac{1-E_{1}\cos(\alpha_{1})}{1-E_{1}\cos(\alpha_{2})} [2]$$
Notice that the terms of coil sensitivity and the T₂* decay, i.e. C and $$$e^{-TE/T_2^*}$$$, are both cancelled out in Eq.2, indicating S_aT1W is independent of coil sensitivity and echo time. To incorporate the MDI strategy for S_aT1W calculation on multi-channel GRE data, one can construct and solve the following optimization problem³:
$$ min_{S_{aT1W}}\sum_1^{N_{c}} \parallel S(\alpha_{2})-S(\alpha_{2})\bullet S_{aT1W}\parallel _2^2 [3]$$
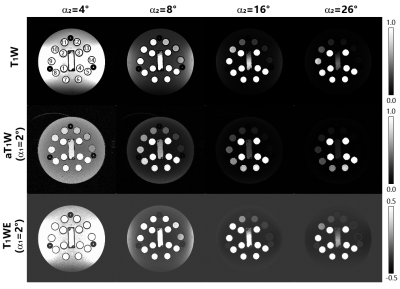
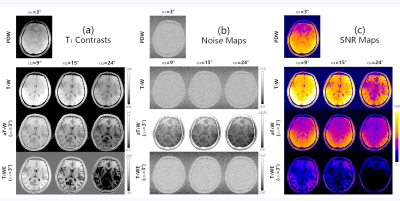
A quantitative phantom (CaliberMRI, Colorado, USA) was used for well-controlled T₁ properties. Phantom T₁W data were acquired using 3D GRE on a 3T system (uMR 790, UIH, Shanghai, China), with a 24-channel head coil. Key scanning parameters included TE/TR =4.9/12.1ms, α₁=2° and α₂ = 4°/8°/16°/26°. With local IRB permission, five healthy volunteers were recruited for brain scans with written consents and passing MRI safety screening. Similarly, single-echo 3D GRE was scanned with: TR/TE=12.1/5.5ms, α₁=3° and α₂=9°/15°/24°, 1mm isotropic voxels with matrix size of 224×190×96 for full brain coverage. Noise propagation maps and SNR maps were also determined for T₁W, aT₁W and T₁WE, as described above. SNR and noise propagation from k-space to the final T₁W/aT₁W/T₁WE images was evaluated in a Monte Carlo manner.

Results

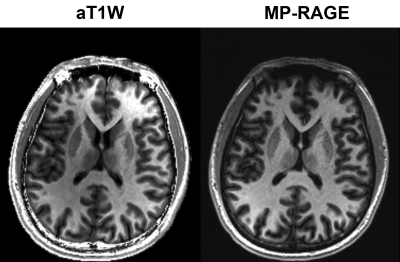
Fig.1 shows simulated signal curves as function of T₁, where aT₁W curve was located between PDW and T₁W curves. Both aT₁W and T₁W curves were monotonic, while the T₁WE curve was non-monotonic. Fig.2 shows phantom images, where 2° flip angle (i.e. α₁) yielded PDW images and higher flip angles (i.e. α₂) for T₁W images. Fig.3 shows the T₁ contrast comparison of brain scans, with additional comparison on noise propagation and SNR maps. For both phantom and brain scans, higher α₂ led to stronger contrasts for all results. aT₁W image remained homogeneous regardless for all α₂ results, while T₁W and T₁WE images were non-uniform. Also, there were zero or even negative values in T₁WE images. It is more clearly shown in Fig.3 that the SNR maps of aT₁W were insensitive to the choice of flip angles, while those of T₁W and T₁WE varied by flip angles. Fig.4 indicates that aT₁W images has very similar T₁ contrast to T₁ FLAIR.

Discussion & Conclusion

The reasons for the proposed aT₁W method to achieve improved T₁ contrast are two-fold: yielding pure T₁ weighting effects via removal of non-T₁ effects, and SNR boost via the complex signal MDI processing strategy⁴. The intrinsic aT₁W contrast (i.e. $$$\frac{1-E_{1}\cos(\alpha_{1})}{1-E_{1}\cos(\alpha_{2})}$$$) is no stronger than the intrinsic T₁W contrast (i.e. $$$\frac{1-E_{1}}{1-E_{1}\cos(\alpha_{2})}$$$) as indicated in Fig.1. However, GRE signals are also modulated by proton density, T₂* relaxation, and receiver coil sensitivity and B₁ fields. Such non-T₁ effects are all present in T₁W and T₁WE signals while being mostly removed in aT₁W signals. Therefore, the observed contrast improvement in aT₁W stems from the removal of non-T₁ effects, including PD, T₂* and coil sensitivity effects, thus revealing pure T₁ weightings. Both aT₁W and T₁W signals are monotonic to produce correct T₁ contrast regardless of scanning parameters. However, T₁WE signals display non-monotonic behaviors, depending on T₁ values and the flip angle α₂. Although offering exceptional contrasts in short T₁ ranges, the T₁WE contrast quickly diminishes and even become negative at longer T₁ values. Therefore, restriction on the choice of flip angles and employing B₁ field correction³ will be required for T₁WE, which poses limitations on potential applications. As MDI is most fit for use with division operation³, it can be directly applied for calculation of aT₁W for SNR boost and efficient computation.
In conclusion, we have proposed an aT₁W contrast based on simple division operation. With the use of MDI technique, aT₁W images offer improved and homogeneous T₁ contrast, high SNR and consistent performance over arbitrary imaging parameters. It can be beneficial in the context of multi-contrast imaging techniques, as well as any clinical application involving T₁ contrast.

Acknowledgements

No acknowledgement found.