Synopsis

Constrained alternating minimization for parameter mapping (CAMP) improves the image quality in highly accelerated parameter mapping by incorporating a linear constraint that relates consecutive images.

Introduction

While qualitatively weighted images, such as T2w-images, are powerful clinical tools, quantitative parameter maps may have many advantages as they show greater consistency across multi-site studies ¹, which allows for universal diagnostic criteria and more robust analyses. However, protocols for quantitative imaging can be difficult to deploy in many clinical settings because accurate parameter maps require several images for relaxometry exponential fitting, leading to long scan times. CAMP (Constrained Alternating Minimization for Parameter mapping) is a reconstruction approach that alternates between optimizing the image series and the parameter map, but it does so by minimizing a single cost-function that incorporates both (1) consistency between each individual parameter image and its k-space data and (2) adherence of the image series to a linear relaxometry model for each pixel. While proof-of-principle for this method was reported previously ², the current results provide quantitative analysis, simulations examining the effect of noise, and comparison to other TE-regularized reconstruction approaches. CAMP is studied in both undersampled radial and Cartesian acquisition schemes.

Methods

CAMP
In MR parameter mapping, the complete MRI signal vector $$$S(k)$$$ is regarded as a series of signal vectors $$$S_p (k)$$$, each of which samples the k-space $$$k$$$ of a complex weighted image $$$m_p$$$ acquired at different parameter encoding values (e.g., echo time TE), through the encoding matrix $$$E_p$$$ for a total of $$$p$$$ images, where $$$p$$$ is also the number of echo times sampled.
As described in ², the relationship of each parameter map relative to the previous one is $$$m_{(p+1)} (x)=m_p (x)α(x),$$$ where $$$α(x)=exp(\frac{-p∆TE}{T_2 (x)})$$$. Our objective function can be described by $$$J=J_1+J_2+J_3$$$, where $$$J_1=∑_{(p=1)}^P‖S_p-E_p m_p ‖^2$$$ is the data fidelity term, $$$J_2=τ∑_{(p=1)}^PTV(m_p )$$$ is a TV-norm regularization term, and finally, $$$ J_3=λ∑_{(x=1)}^N∑_{(p=1)}^{(P-1)}‖m_{(p+1)} (x)-α(x) m_p (x)‖^2 $$$ is the CAMP constraint. $$$τ$$$ and $$$λ$$$ are both weighting parameters. The CAMP objective function $$$J$$$ is alternately minimized with respect to $$$m_p$$$ (fixed $$$α$$$) using a non-linear conjugate-gradient method (Polak-Ribiere). ³ It is then minimized with respect to $$$α$$$ (fixed $$$m_p$$$), keeping in mind that $$$α$$$ is real.
Imaging
Radial and Cartesian data were acquired on a 3T MRI scanner (MAGNETOM Trio Tim, Siemens Healthcare, Erlangen, Germany).
I. Radial T2 TSE
T2w-images were acquired using a TSE sequence with TR=2500 ms, TE=25, 50, 75, and 100 ms, with a base-resolution of 128, 128 spokes, 3mm slice thickness, ETL= 4, acquisition time=320 s.
II. Cartesian T2 spin-echo (SE)
T2w-images were acquired using SE sequence with TR=3000 ms, TE=16, 32, 48, 64 ms, with a base-resolution of 128 pixels, 128 k-space lines, acquisition time=384 s, and 3mm slice thickness.
Reconstruction
Undersampling was performed retrospectively to achieve complementary k-space data at each TE. CAMP is compared to regularized CG reconstructions regularized by a TV-norm. In the case of the radial TSE dataset, we also compared CAMP against the k-space weighted image contrast (KWIC) method. ⁴ The two KWIC radii values used in this implementation were 5 and 10 in units of $$$∆k$$$.
Simulation
CAMP reconstruction was simulated using Cartesian data where a T2-template and a proton-density (PD) template were used to simulate ten T2w-images. Different levels of random complex Gaussian-noise are added to the k-space of those images.
Assessment
The quality of the reconstructed map using the undersampled k-space was assessed using normalized-root-mean-square-error (NRMSE) and high-frequency-error-norm (HFEN). ⁵

Results

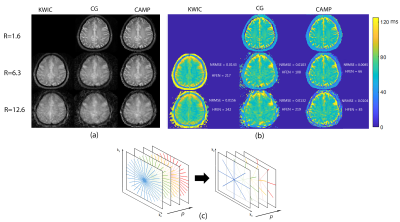
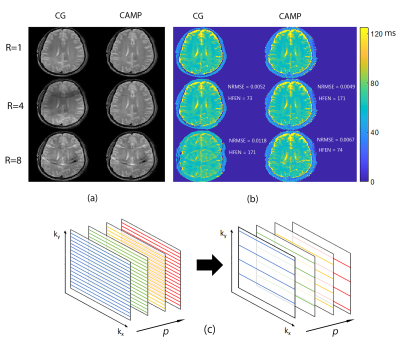
Figure 1 shows T2w-images (TE=75 ms, Figure 1a) and T2-maps (Figure 1b) reconstructed from radial TSE data. The leftmost column of Figure 1a shows T2w-images with KWIC reconstruction using undersampling factors R of 6.3 and 12.6. The columns in each panel correspond to KWIC reconstruction, CG reconstruction using just the data acquired at each echo, and CAMP reconstruction, respectively. At each undersampling (2^nd and 3^rd row), CAMP has improved image quality compared to the CG and KWIC reconstructed images. When R=12.6 (3^rd row), CAMP reconstruction reduced the NRMSE error by 21% and the HFEN by 61% relative to those of CG. While CAMP reduced the NRMSE and by 33% and the HFEN by 65% relative to those of KWIC.
Figure 2 compares reconstructions for fully and undersampled Cartesian T2-mapping. Using CG reconstruction, the coherent Cartesian undersampling artifacts are slightly apparent for example in the TE= 48 T2w-image, while these artifacts are suppressed with CAMP. For example, at R=8 (3^rd row), CAMP reconstruction reduced the NRMSE error by 43% and reduced the HFEN by 56% relative to those of CG.
The simulation results shown in Figure 3 demonstrated that CAMP is robust under different undersampling conditions. With different undersampling factors R=1, 2, 4, after adding to the k-space data random Gaussian-noise with 0 mean and standard-deviation σ=100% of the signal arithmetic mean, the noise was not overly amplified in any area of the resulting T2-map. As expected, the NRMSE errors were proportional to the undersampling and added noise, as demonstrated in Figure 4.

Discussion and Conclusion

While this work shows just a few examples, CAMP is also applicable to any kind of spatial encoding or undersampling scheme. Significantly, this means that while CAMP is a general approach to reconstruct a wide array of MR parameter mapping strategies, it maintains the accuracy of using a signal model anchored in the physics of the acquisition.

Acknowledgements

We note that both Dr. Galiana and Dr. Tagare contributed equally as senior authors on this work. This work was funded by the National Institutes of Health under R01EB022030, R01EB012289, 4R01 EB016978, and K01EB16897.