2599
MEDI-d: Downsampled Morphological Priors for Shadow Reduction in Quantitative Susceptibility Mapping
Alexandra Grace Roberts1,2, Pascal Spincemaille2, Thanh Nguyen2, and Yi Wang2,3
1Electrical and Computer Engineering, Cornell University, Ithaca, NY, United States, 2Radiology, Weill Cornell, New York, NY, United States, 3Biomedical Engineering, Cornell University, Ithaca, NY, United States
1Electrical and Computer Engineering, Cornell University, Ithaca, NY, United States, 2Radiology, Weill Cornell, New York, NY, United States, 3Biomedical Engineering, Cornell University, Ithaca, NY, United States
Synopsis
Morphology Enabled Dipole Inversion (MEDI) is an iterative reconstruction algorithm for Quantitative Susceptibility Mapping (QSM) that is effective in suppressing streaking artifacts by exploiting the magnitude image as a morphological prior. However, contiguous areas of dipole incompatibility (such as noise) induce shadow artifacts whose spatial frequency components are not adequately regularized by the gradient based regularization in MEDI. Here, we show the feasibility of adding a downsampled morphological prior to suppress these shadow artifacts.
Introduction
Quantitative Susceptibility Mapping (QSM) is an MRI contrast mapping the magnetic susceptibility of tissue in vivo from gradient echo measurements. The inverse problem in QSM is ill-posed requiring the use of regularization. Bayesian inference approaches such as Morphology Enabled Dipole Inversion (MEDI) use an edge weighted gradient under an $$$L^1$$$ norm to penalize the streaking artifacts arising from dipole-incompatible sources (such as noise) in the phase of the gradient echo data1,2. However, larger contiguous areas of dipole-incompatibility may exist in the phase such as low signal regions in bone or air and residual background field whose source is outside the region of interest. These induce shadow artifacts that are less effectively suppressed by this regularization. Exploiting the Spherical Mean Value (SMV) property of the harmonic background field3 and including it in the dipole kernel (MEDI-SMV) suppresses many of these artifacts at the cost of an eroded brain mask. In this work, we propose adding a downsampled morphological prior to suppress these shadow artifacts.Methods
The cost function in MEDI4 is $$χ(r)=argminχ‖w(e^{ib}-e^{(id*χ)} )‖_2^2+λ‖M∇χ‖_1\tag{1} $$ Where $$$b$$$ is the relative difference field, $$$d$$$ the dipole kernel, $$$χ$$$ the susceptibility, $$$w$$$ the noise weighting matrix, $$$M$$$ morphological weighting matrix, and $$$∇$$$ the gradient. By considering that shadow originating from larger dipole incompatible sources can be viewed as streaking artifacts of those same source in a lower resolution image, we propose adding a second edge regularization term that acts on a downsampled version of the susceptibility weighted by a similarly downsampled edge weight: $$χ(r)=argminχ‖w(e^{ib}-e^{(id*χ)} )‖_2^2+λ_1 ‖M∇χ‖_1 +λ_2 ‖M_S ∇Sχ‖_1\tag{2}$$ where $$$S$$$ is a downsampling operator and $$$M_S$$$ is the edge mask derived from the downsampled image $$$S_m$$$ with $$$m$$$ the sum of squares across echoes of the gradient echo signal using the same method in which $$$M$$$ was derived from m. The downsampling operator was implemented in Fourier space by cropping the central $$$\frac{N_x}{α}×\frac{N_y}{α}×\frac{N_z}{α}$$$ portion of k-space with $$$α$$$ the downsampling factor and $$$N_x×N_y×N_z$$$, the size of $$$b$$$. A Hanning window was applied to the cropped k-space array to reduce Gibbs ringing. A comparison between the original $$$M$$$ and downsampled $$$M_S$$$ weights is shown in Figure 1. The resulting method is termed as MEDI-d.4 healthy volunteers (eight men, two women, mean 32 ± 6 years of age) were scanned twice at 3T (GE Healthcare) using a 3D multi-echo spoiled gradient echo sequence. Acquisition parameters were FOV = 24 cm, partial FOV factor = 0.8, acquisition matrix size = 384 × 384 × 64, flip angle = 20°, slice thickness = 2 mm, TR = 52 msec, number of echoes = 11, first TE = 4.1 msec, echo spacing = 4.4 msec, parallel imaging factor 2, scan time of ~8 minutes. Additional reconstructions were performed for the in vivo dataset taken from the freely available data included with the MEDI Toolbox. Its acquisition parameters were similar but used a 256 × 256 × 74 matrix. The regularization parameter and downsampling factor were varied to find the minimum root mean square error (RMSE) with respect to the MEDI SMV recon. The RMSE measure was modified by weighting high susceptibility values stronger using a sigmoid function. Deep gray matter ROIs were drawn on this dataset by an experienced reader and mean values were compared across methods and reconstruction parameters.
Results
Figure 2 shows the influence of the regularization parameter $$$λ_2$$$ on the image quality, with decreasing shadow as the regularization is stronger at the cost of decreased contrast. Figure 3 shows the influence of the regularization parameter $$$λ_2$$$ and downsampling factor α on the RMSE according to MEDI SMV in one healthy subject. The obtained minimizers of $$$λ_2=250$$$ and $$$α=3$$$ were used for all reconstructions. Figure 4 shows the ROI analysis. The chosen parameters lead to deep gray matter ROI values that are similar or slightly lower than those obtained using MEDI and MEDI-SMV.Conclusion
The downsampling regularization term is effective at reducing shadows by more heavily penalizing internal edges in the reconstructed susceptibility. Future work will include healthy subject error calculations, k-space cropping scheme optimization, and reconstruction augmentation.Acknowledgements
No acknowledgement found.References
- Y. Kee et al., “Quantitative susceptibility mapping (QSM) algorithms: Mathematical rationale and computational implementations,” IEEE Trans. Biomed. Eng., vol. 64, no. 11, pp. 2531–2545, 2017.
- J. K. Choi, H. S. Park, S. Wang, Y. Wang, and J. K. Seo, “Inverse problem in quantitative susceptibility mapping,” SIAM J. Imaging Sci., vol. 7, no. 3, pp. 1669–1689, 2014.
- Y. Wen, D. Zhou, T. Liu, P. Spincemaille, and Y. Wang, “An iterative spherical mean value method for background field removal in MRI: Robust Background Field Removal Using iSMV,” Magn. Reson. Med., vol. 72, no. 4, pp. 1065–1071, 2014.
- J. Liu et al., “Morphology enabled dipole inversion for quantitative susceptibility mapping using structural consistency between the magnitude image and the susceptibility map,” Neuroimage, vol. 59, no. 3, pp. 2560–2568, 2012.
- P. S. Balasubramanian, P. Spincemaille, L. Guo, W. Huang, I. Kovanlikaya, and Y. Wang, “Spatially adaptive regularization in Total Field Inversion for quantitative susceptibility mapping,” iScience, 23(10), p. 101553, 2020.
Figures
Figure 1. Original structural weighting matrix
(left) and downsampled structural weighting matrix (right) in the $$$x$$$-direction. Note
that the white regions (equal to 1) enforce edge requirements on the
susceptibility solution while the black regions (equal to 0) do not.
Figure 2. Central slice of control MEDI, MEDI-d with a downsampling factor of 2 and 3 different
regularization parameters, and MEDI-SMV. Note the reduction of shadowing causes
loss of detail that occurs beyond $$$\lambda_2$$$ = 1000.
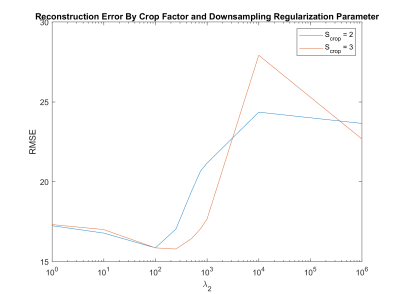
Figure 3. RMSE according to MEDI SMV. A sigmoid weighting function was used to preserve anatomical detail.
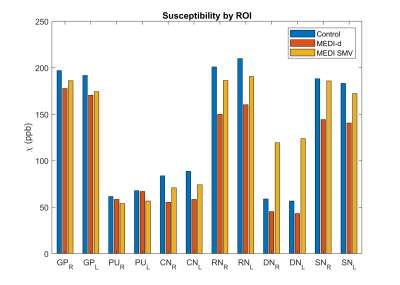
Figure 4. ROI susceptibility by reconstruction algorithm for control, optimal MEDI-d, and
MEDI SMV.
Figure 5. Healthy subject 3 control, MEDI-d with $$$\lambda_2$$$ =250, and MEDI-SMV reconstructions.
Figure 6. Healthy subject 4 control, MEDI-d with $$$\lambda_2$$$ =250, and MEDI-SMV reconstructions.
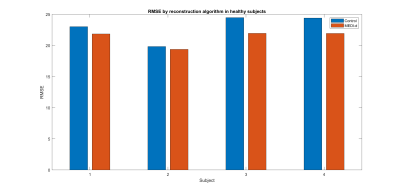
Figure 7. RMSE of control and MEDI-d with $$$\lambda_2$$$ =250, according to MEDI SMV.