Introduction

Accurate unaliasing in accelerated image reconstruction often relies on consistency of the undersampled acquisition with some reference calibration data¹. However, this assumption can be violated in a number of different ways, including by bulk motion, significant contrast changes, or fluctuating B0 field inhomogeneities. The last factor is an especially important source of artefacts in fMRI of awake non-human primates (NHPs), where significant unpredictable field inhomogeneities are caused by body movements that are likely to occur even if the head is fixed. Hence, estimating dynamic field perturbations and incorporating them in the reconstruction framework can reduce ghosting and residual aliasing artefacts that are not addressable in post processing.

Recently, multi-channel free induction decay navigators (FIDnavs) have been used to successfully estimate low‐spatial‐order dynamic field changes in fMRI². However, utilising FIDnavs requires sequence modification, and generating an accurate forward model that depends on extra reference images that should be acquired with contrast parameters matched to the navigator, which might be difficult to achieve in some scenarios.

To mitigate these issues, we used reference EPI navigators to estimate dynamic field perturbations, without the need for contrast-matched reference images. These short navigators that sample the central line of k-space three times at each TR are already present in typical EPI sequences for correcting Nyquist ghost artefacts. Here, we used the spatial encoding provided by multi-channel navigators to estimate first order field perturbations in every TR. Field estimation quality is demonstrated in phantom and in vivo experiments, and improved reconstruction performance through significant reduction of residual aliasing is demonstrated using simulations of accelerated fMRI in NHPs.

Methods

As described in (3), $$$N_c\times N_c$$$ GRAPPA operators can be trained on calibration data to predict each k-space point using one adjacent sample on the Cartesian grid from $$$N_c$$$ channels. Letting ($$$G_x,G_y$$$) be the operators and ($$$\Delta_x,\Delta_y$$$) be grid spacing across x and y directions, arbitrary shifts of k-space data $$$S$$$ can be realised using fractional powers of the operators³:

$$S(k_x+\delta_x,k_y+\delta_y)=G_x^{\delta_x/\Delta_x}G_y^{\delta_y/\Delta_y}S(k_x,k_y)$$

Letting $$$s_j^n(t)$$$ be the channel $$$j$$$ navigator signal at frame $$$n$$$, signal at the reference frame ($$$n=0$$$) is expressed as:
$$s_j^0(t)=\int_x\int_y\rho_j(x,y)e^{-j2\pi[k_x(t)x+k_y(t)y]t}e^{-i\Delta\omega^0t}dxdy$$
where $$$\rho_j$$$ is the coil-sensitivity-encoded object magnetisation, and $$$\Delta\omega$$$ is the off-resonance. Field perturbations in NHP fMRI are mainly caused by motion in body parts that are distant from the imaging volume, and have low spatial frequency⁴. Hence, off-resonance at frame $$$n$$$ can be modelled as a linear spatial perturbation superimposed on the off-resonance at the reference frame:

$$\Delta\omega^n=\Delta\omega^0+2\pi[b_xx+b_yy]$$

yielding the navigator signal as:

$$s_j^n(t)=\int_x\int_y\rho_j(x,y)e^{-j2\pi[[k_x(t)+b_x]x+[k_y(t)+b_y]y]t}e^{-i\Delta\omega^0t}dxdy$$

Linear field perturbation is thus manifested as linear shifts in k-space:

$$S_j^n(k_x,k_y)=S_j^0(k_x+b_x,k_y+b_y)$$

where $$$S_j^n$$$ is the k-space data at frame $$$n$$$.

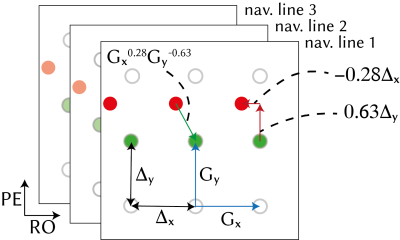
We modelled the shifted k-space data from the multi-channel three-line navigators using GRAPPA operators (illustrated in Fig.1):

$$\begin{bmatrix}S_{j,1}^n\\S_{j,2}^n\\S_{j,3}^n\end{bmatrix}=\begin{bmatrix}G_x^{\alpha}G_y^{\beta}&0&0\\0&G_x^{\alpha}G_y^{\beta}&0\\0&0&G_x^{\alpha}G_y^{\beta}\end{bmatrix}\begin{bmatrix}S_{j,1}^0\\S_{j,2}^0\\S_{j,3}^0\end{bmatrix}$$

and solved for $$$\alpha=b_x/\Delta_x$$$ and $$$\beta=b_y/\Delta_y$$$ using data from $$$N_c$$$ channels. Nelder-Mead simplex gradient-free nonlinear solver was used⁵. To improve numerical stability, only the five central k-space samples were used.

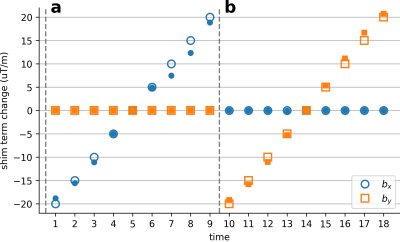
To examine the perturbation estimation accuracy, a bottle phantom was scanned on a 3T scanner using a 15-channel NHP receive coil and an EPI sequence with parameters: TE/TR= 30/2000ms,FA=90,FOV=192mm,1.5mm isotropic resolution. To mimic dynamic field perturbations, separate scans were performed where first-order shim terms (X,Y) were manually adjusted up to ±20μT/m in 5μT/m increments across scans.

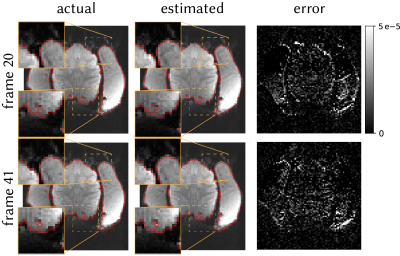
To test the method in vivo, we acquired 50 frames of brain data from an awake macaque monkey using scan parameters matched to the phantom scan. We estimated field perturbation at each TR and distorted the fully-sampled reference using conjugate-phase reconstruction (CP)⁶. We then compared the distorted and acquired frames.

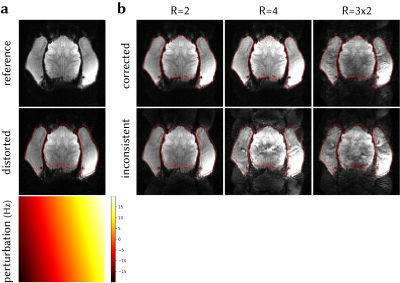
To demonstrate the effect of calibration inconsistency correction on reducing residual ghosting and unaliasing artefacts, data and navigators at the reference frame were distorted via CP, assuming a linear field perturbation (0.00±9.62Hz, mean±std across the FOV). Perturbation was estimated and data were corrected via inverse operators. Inconsistent and corrected frames were retrospectively undersampled at R=2,4 and GRAPPA-reconstructed. Multiband data were simulated with MB=2,R=3 by collapsing the data across slices and reconstructed using split-slice-GRAPPA⁷.

Results

Figure 2 shows the shim terms estimated on the phantom. Modulated shim terms are accurately estimated, with absolute error of 0.56±0.10μT/m (mean±sem across frames).

Figure 3 shows the estimated distortions in vivo for two representative frames. The method accurately estimates the distortions in vivo.

Figure 4 shows the effect of field perturbation leading to calibration inconsistency, and correcting for it, on the accelerated reconstructions. Considerable ghosting artefacts arise from calibration inconsistency that cannot be corrected in post processing. The proposed method corrects the inconsistency, reduces artefact power, and corrects for geometric distortion in a single step.

Discussion and Conclusion

Calibration inconsistency due to dynamic field perturbations leads to significant aliasing artefacts when scanning awake behaving NHPs. To address this, we propose a method to estimate field perturbations using GRAPPA operators that does not require sequence modification or extra acquisitions. The method accurately predicts field perturbations in phantom and in vivo NHP data. We also demonstrate significant artefact reduction in synthesised accelerated EPI acquisitions by estimating and correcting the perturbations. The proposed improvements make highly accelerated awake behaving NHP imaging more robust and reliable, reducing the gap between what is possible with NHP protocols and state-of-the-art human imaging.