2517
Comparison of pharmacokinetic models for assessing murine renal function by DCE-MRI1Centre for Preclinical Imaging, University of Liverpool, Liverpool, United Kingdom, 2Department of Cellular and Molecular Physiology, University of Liverpool, Liverpool, United Kingdom, 3Department of Mathematical Sciences, University of Liverpool, Liverpool, United Kingdom
Synopsis
Quantitative analysis of kidney function is essential part of monitoring disease progression. The most common parameter of evaluating kidney functioning is by measurement of glomerular filtration rate. Here, we describe that dynamic contrast enhanced magnetic resonance imaging can be used to determine the permeability parameter Ktrans, which can be used to assess renal activity. We used three different pharmacokinetic models and arterial input functions to get the Ktrans value. It was seen that the raw arterial input function used along with shutter speed model has strong correlation with findings obtained from transcutaneous GFR measurement device.
Introduction
A key function of the kidney is to excrete waste and excess fluid. The nephron is responsible for filtration in the kidney and is comprised of the glomerulus across which ultrafiltration occurs. The current gold standard for measuring kidney function is by estimation of the glomerular filtration rate (GFR) using inulin or chromium ethylenediaminetetraacetic acid (Cr-EDTA) clearance rate measured from serial blood samples. However, this invasive and time consuming procedure provides no spatial information about organ function within the kidney 1. Several alternative non-invasive approaches have been established including preclinical transcutaneous measurements of GFR which are based on the elimination kinetics of fluorescent exogenous markers 2,3. However, these assays only provide a global GFR value and do not provide any spatial information about the kidney. DCE data from the kidney can be analysed using pharmacokinetic (PK) models to estimate GFR 4 , however, the application of these to murine models of kidney disorders is not common and also these models lack the reproducibility required for clinical application 5. Mouse kidney DCE-MRI poses challenges due to respiratory motion, difficulty in measuring the arterial input function (AIF), and accumulation of contrast agent in the renal pelvis resulting in fast T2* relaxation and consequent signal loss. With several competing PK models in use, it is not evident as to which model is most appropriate for analysis of renal DCE data. In this study we compared three commonly used PK models: non-linear Tofts ; extended Tofts; and the shutter speed model (SSM). These models have been used in brain tumours 6-8. While non-linear Tofts is computationally less taxing, it has precision and fitting accuracy 8. Extended Tofts improves upon the non-linear model but is inconsistent for high temporal resolution data 9. SSM takes into consideration the transcytolemmal water exchange which plays an important role in kidney function10. The parameter Ktrans is a transfer coefficient estimating the capillary permeability rate. Ktrans multiplied by the kidney volume is typically used to compute GFR.Methods
Wild-type female C57BL/6 mice (n=9) were anaesthetized using 1.5-2.0% isoflurane in oxygen. MR measurements were carried out on a 9.4 T scanner using an 86 mm birdcage transmit coil and 4-channel receive array (Bruker, Germany). Mean T1 values of the kidney cortex were measured using an inversion recovery pulse sequence. A catheter (30G needle with poly-ethylene tubing) was inserted into the tail vein and filled with heparin solution. A bolus of Gd-BOPTA (Multihance, Bracco Diagnostic Inc., Italy) was injected through the catheter (50 µl, 0.1 mmol/kg). A single slice, dual-echo gradient echo sequence was used for DCE imaging (TR/TE1/TE2=15.43/1.26/6.99 ms, 25° flip angle, 192x96 matrix, 40x20 mm FOV, 987 ms temporal resolution). Mean kidney volume was calculated from multi-slice T2-weighted images for GFR measurements. DCE-MR images were processed off-line using in-house software written in Matlab (Mathworks, USA). As the AIF is critical to quantitative analysis of DCE data and is difficult to measure in mice, three methods of estimating AIF were tested and their effects on PK model parameters was assessed. AIF was estimated using the raw data, a singular spectrum analysis (SSA) denoising algorithm11 and a fitted bi-exponential curve. For parametric model analysis and parameter extraction, Ktrans derived from non-linear, extended Tofts and SSM were used, while for τi values, SSM was used using a non-linear least-squares fitting based Levenberg-Marquardt algorithm. Initial fitting parameter values were selected based on literature 10,12.Results
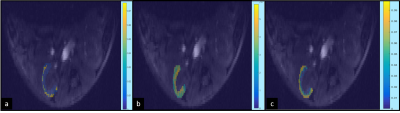
Figure 1 shows three representative Ktrans maps from a left renal cortex overlaid on a corresponding anatomical image; the maps were generated using the three PK models and the AIF derived from the raw imaging data. The boxplots in Figure 2 demonstrate the mean Ktrans values from the nine mice measured for the three PK models and the three AIF models used. A significant difference in the Ktrans value (p<.05, Figure 2) was observed using the extended Tofts model when compared with the other models, while using the denoised AIF. On the other hand, Ktrans using the original and the biexponential fitted AIF had no significant difference on the measured Ktrans values using the three models. Ktrans estimated using the AIF derived from the raw data demonstrated the least variability.Discussion
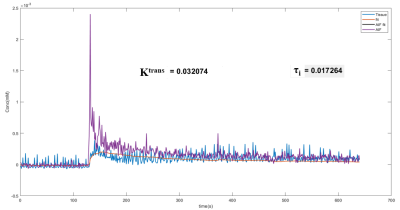
The GFR values derived from Ktrans estimated using the SSM (1416 ± 189 µl. min-1 100 g body wt-1) were matching the GFR values from the literature (1381 ± 264 µl min-1 100 g body wt-1) 2, whilst the Ktrans from the non-linear and extended Tofts underestimated the GFR values indicating that SSM is the most appropriate model under these experimental conditions. In addition, SSM estimates the value of τi providing a window into cellular metabolism. The SSM-derived τi value was found to be very low which is shown in the voxel-wise analysis of the cortex of the kidney as seen in figure 3.Conclusion
These results demonstrate that using the AIF derived from the raw data along with SSM provides a consistent and accurate estimate of Ktrans from the mouse kidney. Ktrans promises to be a useful measure of renal function and GFR, thus enabling localised assessment of renal function in the presence of heterogeneous/focal kidney injury, such as the ischemia-reperfusion injury.Acknowledgements
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 813839.References
1. G. Granerus and M. Aurell, “Reference values for 51Cr-EDTA clearance as a measure of glomerular filtration rate,” Scand. J. Clin. Lab. Invest., vol. 41, no. 6, pp. 611–616, Jan. 1981.
2. A. Schreiber et al., “Transcutaneous measurement of renal function in conscious mice,” Am. J. Physiol. Physiol., vol. 303, no. 5, pp. F783–F788, Jun. 2012.
3. A. R. Poreddy et al., “Exogenous fluorescent tracer agents based on pegylated pyrazine dyes for real-time point-of-care measurement of glomerular filtration rate,” Bioorg. Med. Chem., vol. 20, no. 8, pp. 2490–2497, 2012.
4. S. P. Sourbron, H. J. Michaely, M. F. Reiser, and S. O. Schoenberg, “MRI-Measurement of Perfusion and Glomerular Filtration in the Human Kidney With a Separable Compartment Model,” Invest. Radiol., vol. 43, no. 1, 2008.
5. I. Mendichovszky et al., “How accurate is dynamic contrast-enhanced MRI in the assessment of renal glomerular filtration rate? A critical appraisal,” J. Magn. Reson. Imaging, vol. 27, no. 4, pp. 925–931, 2008.
6. A. Bhandari, A. Bansal, A. Singh, and N. Sinha, “Perfusion kinetics in human brain tumor with DCE-MRI derived model and CFD analysis,” J. Biomech., vol. 59, pp. 80–89, 2017.
7. E. Szychot et al., “New trial of convection enhanced drug delivery (CED) in DIPG- applying the SIOPe DIPG survival prediction model for power calculation.,” Neuro. Oncol., vol. 21, no. Supplement_4, pp. iv11–iv11, Oct. 2019.
8. J. F. Kallehauge, S. Sourbron, B. Irving, K. Tanderup, J. A. Schnabel, and M. A. Chappell, “Comparison of linear and nonlinear implementation of the compartmental tissue uptake model for dynamic contrast-enhanced MRI,” Magn. Reson. Med., vol. 77, no. 6, pp. 2414–2423, Jun. 2017.
9. S. B. Donaldson et al., “A comparison of tracer kinetic models for T1-weighted dynamic contrast-enhanced MRI: application in carcinoma of the cervix.,” Magn. Reson. Med., vol. 63, no. 3, pp. 691–700, Mar. 2010.
10. M. Inglese et al., “Reliability of dynamic contrast-enhanced magnetic resonance imaging data in primary brain tumours: a comparison of Tofts and shutter speed models,” Neuroradiology, vol. 61, no. 12, pp. 1375–1386, 2019.
11. R. Vautard and M. Ghil, “Singular spectrum analysis in nonlinear dynamics, with applications to paleoclimatic time series,” Phys. D Nonlinear Phenom., vol. 35, no. 3, pp. 395–424, 1989.
12. X. Li, W. D. Rooney, and C. S. Springer Jr., “A unified magnetic resonance imaging pharmacokinetic theory: Intravascular and extracellular contrast reagents,” Magn. Reson. Med., vol. 54, no. 6, pp. 1351–1359, Dec. 2005.
Figures