2487
Motion and Pose Variability of SAR Estimation with Parallel Transmission at 7T1Biomedical Engineering Department, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 2Centre for the Developing Brain, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 3MR Research Collaborations, Siemens Healthcare Limited, Frimley, United Kingdom
Synopsis
Contemporary safety assessment for parallel transmit (pTx) MRI relies on computationally expensive electromagnetic (EM) simulations; hence, safety evaluations rely on the use of small numbers of models. The effect of patient movement inside the coil on patient safety is, therefore, difficult to capture. In this work we compare 'within-scan' variability with the alternative scenario in which a subject’s head is positioned arbitrarily within the coil, but that this position is different to the one used for the SAR estimation model; we refer to this as ‘pose’ variability.
Introduction
Contemporary safety assessment for parallel transmit (pTx) MRI relies on computationally expensive electromagnetic (EM) simulations; hence, safety evaluations rely on the use of small numbers of models (body, coil, or coil position with respect to body). The effect of patient movement inside the coil on patient safety is, therefore, difficult to capture, though initial studies have been conducted[1]. Kopanoglu investigated the effect of motion with 6 DOFs, focusing on variability from within-scan patient head motion,i.e. the pTx system is configured at the start of the scan, and variability is tracked thereafter.In this work we compare 'within-scan' variability with the alternative scenario in which a subject’s head is positioned arbitrarily within the coil, but this position is different to the one used for the SAR estimation model; we refer to this as ‘pose’ variability.
Methods
In order to efficiently model motion/pose variability we used the recently proposed magnetic resonance integral equation (MARIE) formalism[2], including implementation of the Magnetic Resonance Green’s Functions (MRGFs). MRGFs(Fig.1) can be pre-computed within a coil ‘region’ and can then be used to very quickly evaluate the fields from any coil within this region. Although initially intended to allow fast evaluation of new coil designs, we have used this feature to explore position sensitivity by translating and rotating the coil within this region, therefore creating relative motion between the coil and human body model.Any RF coil fitting in this domain can be simulated. In this work we constructed a 4-channel coil array with rectangular loops, each with 5 capacitors, 1 driving port and a matching circuit. An implementation of circuit-co-simulation[4,5] was used to find the capacitor values to decouple the coils and tune and match to 298 MHz(7T). Ultimately, the coil was displaced randomly across 6 DOFs providing a total of 121 coil positions with respect to the head. For each perturbation, B1+fields and Q-matrices were computed. In some positions we performed RF shimming to compute optimal amplitude and phase settings to give uniform B1+ for a mid-axial slice through the brain. RF shimming used the magnitude least squares (MLS) method [3] with regularization to penalise high power solutions.
We separated the study in two parts: A)within-scan motion, B)dependence on initial pose to a fixed model.
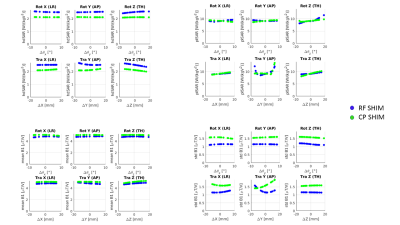
In part A, we apply either a circularly polarized shim or an optimized shim computed for the ‘unperturbed’ coil position. SAR estimates were then made for all perturbations of the coil position to obtain motion-dependent SAR maps.
In part B, we used RF shimming to actively update the shims at every position – mimicking the usual situation in which a person is placed in the scanner, B1+fields are measured and then a scan is run, but the SAR model is not adapted to their position. Hence RF shimming was performed for the B1+maps separately for each position in this scenario. SAR was evaluated in two ways: (i)using the unperturbed SAR model and (ii)using the correct spatially perturbed SAR model. While (ii)is ‘correct’, (i)is what would be done in practice.
In both part A and B, the extracted metrics are: head average SAR(hdSAR), peak local(plSAR), mean B1+ and standard deviation in B1+(stdB1).
Results
The motion study(A) shows that the hdSAR does not change strongly with position for either CP mode or the B1+shim; plSAR does vary more strongly, primarily for rotations about z or AP translations. In these cases, plSAR variation is as high as 50% of the plSAR in the central position. The hdSAR is higher for the B1+shim, while this setting generates lower average B1+, indicating this is a less efficient solution.The pose study(B) instead re-computed B1+shims depending on the B1+fields that would be measured for that head position. These results indicate that SAR can be more variable when accounting for position dependent changes in B1+,but SAR estimates derived from an unperturbed model do not significantly deviate from the true model in most cases.
Discussion
Both the motion and the pose study show low variation in hdSAR, while plSAR was particularly sensitive to translations in the AP direction and rotation around z direction. Kopanoglu similarly shows that the highest variability in head and plSAR in within-scan head-motion is for the displacements in AP direction, and our value of 20% deviation is in agreement with the result reported in that study. Furthermore, motion results in both studies show SAR is more sensitive to translations than rotations.Conclusions
The pose-study produced more stable SAR results than the motion study. In the motion study’s extreme cases where the estimated plSAR is high, the true plSAR is even higher; however, in most scenarios, they are similar. A key observation is that when we calculate an RF shim using a B1+ map from a spatially perturbed position, the resulting SAR estimate using the unperturbed SAR model is often similar to the perturbed case, even when these SAR values differ significantly from that which would result from a shimming calculation at the central position. We hypothesize this is because the B1+ and SAR from the local coil are highly correlated. Further work is needed to determine how this generalises to other coil designs.Acknowledgements
This work is funded by the King’s College London & Imperial College London EPSRC Centre for Doctoral Training in Medical Imaging (EP/L015226/1) and by Siemens Healthineers. This work was supported by the Wellcome EPSRC Centre for Medical Engineering at Kings College London (WT 203148/Z/16/Z) and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy’s and St Thomas’ NHS Foundation Trust and King’s College London. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR, the Department of Health, or the Siemens Healthineers.References
[1] Kopanoglu, E. et al (2020). Specific Absorption Rate Implications of within-scan Patient Head Motion for Ultra-high Field MRI [published online ahead of print, 2020 Apr 17]. Magnetic Resonance in Medicine.
[2] Villena, J F, Polimeridis A G, Eryaman Y, Adalsteinsson E, Wald L L, White J K, Luca Daniel D. (2016). Fast Electromagnetic Analysis of MRI Transmit RF Coils Based on Accelerated Integral Equation Methods. IEEE Transactions on Biomedical Engineering, 63(11), 2250-2261.
[3] Setsompop, K., Wald, L., Alagappan, V., Gagoski, B. and Adalsteinsson, E. (2008). Magnitude least squares optimization for parallel radio frequency excitation design demonstrated at 7 Tesla with eight channels. Magn. Reson. Med., 59: 908-915. https://doi.org/10.1002/mrm.21513
[4] Kozlov M, Turner R. (2009). Fast MRI coil analysis based on 3‐D electromagnetic and RF circuit co‐simulation. J Magn Reson. 200, 147–152.
[5] Beqiri A, Hand J W, Hajnal J V, Malik S J, Comparison between simulated decoupling regimes for specific absorption rate prediction in parallel transmit MRI. Magn. Reson. Med., 74(5), 1423–1434.
Figures
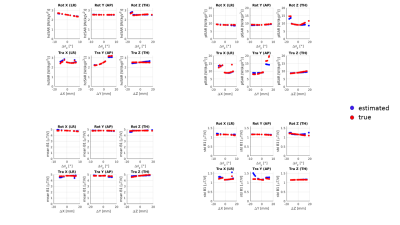
Pose study across all perturbation states for the estimated values (blue) and the true values (red). Top left: head averaged SAR, top right: peak local SAR, bottom left: mean B1+, bottom right: standard deviation of B1+.
The blue points indicate the SAR that would be estimated from an unperturbed model while the red points show the ‘true’ SAR from the true model.