Introduction

Multi-shell diffusion MRI (dMRI) is widely used to inform microstructure studies. Higher spatial resolution is required to fully capture the complex architecture of white matter, while higher angular sampling provides more reliable estimates for the underlying microstructure. However, dMRI is more susceptible to image noise leading to reduced interpretability and quantitative accuracy. Degraded image quality can be compensated by sampling more diffusion encoding directions, or by averaging. However, due to scan time limitations, this is not a practical approach for clinical studies. To accelerate acquisition and explore measurement cardinality (low-rank structure), denoising approaches have been proposed, but denoising can also result in compromised parameter space and unwanted spatial smoothing.
Model based denoising using a generalized spherical deconvolution approach (GenSD) was introduced¹ to accelerate kurtosis imaging with as few as 30 sampling directions. With GenSD, signal at each voxel is modeled as a weighted linear combination of Gaussian basis functions, with the recovery of coefficients formulated as a non-linear optimization. The model operates entirely in diffusion space without spatial regularization, with the benefit that, unlike principal component analysis (PCA)-based techniques, data redundancy does not have to be leveraged for an accurate threshold.
In this study, the parameter space for GenSD was optimized for use with high-performance gradient acquisitions of dMRI data. To establish minimal bias, denoising was compared to a ground truth dataset by evaluating qualitative proof points in the form of neuroanatomical feature retention and quantitative proof points, by evaluating tensor metrics such as fractional anisotropy (FA), and orthogonal kurtosis (OrthoK). Furthermore, to objectively assess variability the stability and reproducibility, tractogram-derived structural connectivity matrices was evaluated.

Methods

Ground-truth dataset was defined as that acquired in a healthy volunteer under an IRB-approved protocol on a 3T MRI system (GE SIGNA MR750, GE Healthcare, Waukesha, WI, USA), equipped with a head-only MAGNUS gradient coil. A 32-channel phased array head coil (NOVA Medical, Wilmington, MA) was used for all acquisitions. The MAGNUS² gradient coil operates at 200mT/m with a maximum slew rate of 500T/m/s using standard clinical 1MVA system electronics. A multi-shell acquisition was utilized with 45,60,80, and 100 directions with points distributed such that the sampling pattern minimized the energy of electrostatic repulsion for points on a sphere³, for b-values of 500,1000,2000, and 4000 s/mm². An additional 16 non-diffusion weighted (T₂-weighted,b=0) images were interspersed through the acquisition. For TE/TR=44.2/7000ms, 160x160x86 matrix, diffusion data were acquired with an isotropic resolution of 1.5x1.5x1.5 mm³ with an overall acquisition time of 30min.
Diffusion weighted images were corrected for gradient non-linearity, eddy-current distortion, bulk motion and susceptibility using an in-house image processing pipeline. Accelerated acquisitions were generated by deriving candidate subsets from ground-truth, by drawing the desired number of directions to maximize angular incoherence³, while preserving the rotationally invariant properties⁴.
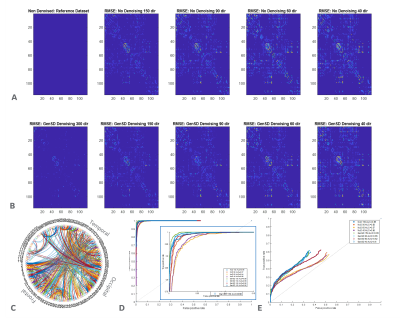
GenSD denoising, was applied to all the subsets. Diffusion and kurtosis tensors were fitted using an iterative weighted least-squares approach to compute FA and OrthoK. Fiber orientation distribution functions (fODFs) were computed using mrtrix⁵, by estimating tissue response using the Dhollander algorithm, and implementing multi-shell multi-tissue CSD⁵. WM constrained probabilistic tractograms were generated for all datasets using the iFOD2⁶ algorithm with dynamic seeding. Edge metrics for connectivity matrices, generated from the tractograms and node parcellation using automated anatomical labeling(AAL: 116 parcels), were defined either by streamline count and filtered to reduce bias via the SIFT algorithm⁷ or by mean streamline length, scaled by the inverse of the two node volumes⁸. A binary connectivity determination between ground truth and denoised accelerated datasets was used to generate receiver-operating-characteristic (ROC) curves to characterize performance, further compared using the area-under-the-curve (AUC) metric.

Results and Discussion

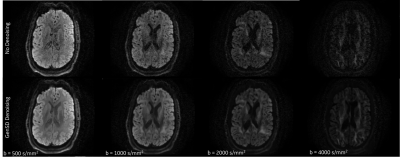
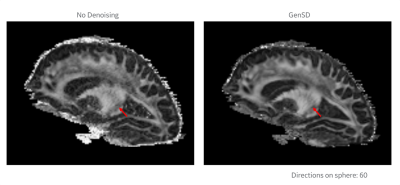
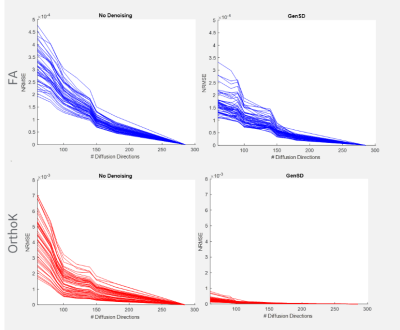
Qualitative assessment highlights that model-based denoising did not compromise spatial structure (Figure 1). Even with accelerated acquisitions of 60-directions, fine striatal cell bridges can be recovered with denoising (Figure 2). Because of the model’s high degrees of freedom (3-anisotropic & 70-isotropic compartments), with accelerated acquisitions, quantitative metrics are marginally impacted evidenced by bias reduction (Figure 3) compared to no denoising on board. Kurtosis, mostly constrained by high b-value data, is particularly sensitive to noise, thus the derived data benefits significantly from genSD denoising (Figure 3). Importantly, as the sample size was decreased, the bias reduction allowed for a corresponding ~2-3x reduction in scan time compared to ground truth.
With connectivity measures, false streamlines are of great concern. Particularly after denoising, there is a need to ensure the data is not being altered. Comparison to ground truth and denoising was initially based on a simple threshold of whether connections were altered, with denoising indicating a slightly higher true positive rate for ROC curves, and RMSE in connectivity plots (Figure 5). The impact of streamline length on tractography is well reported, where generally longer bundles are over-represented, and smaller harder-to-track bundles are underrepresented. As error propagates, long streamlines can propagate from one bundle to another creating an artificial bundle, ergo, the longer the track the less reliable its trajectory. A more quantitative analysis to build a distribution of these differences is in progress.

Conclusions

Combined with GenSD denoising, acquisition time can be accelerated ~2-3x while preserving fine anatomical details and establishing minimal bias in tensor-derived metrics with slight stability in structural connectivity analysis.

Acknowledgements

Grant funding from NIH U01EB28976, CDMRP W81XWH-16-2-0054