2475
Reducing Noise in Complex-Valued Multi-Channel Diffusion-Weighted Data via Optimal Shrinkage of Singular Values
Khoi Minh Huynh1,2, Wei-Tang Chang2, and Pew-Thian Yap1,2
1Biomedical Engineering, UNC Chapel Hill, Chapel Hill, NC, United States, 2Department of Radiology and Biomedical Research Imaging Center (BRIC), UNC Chapel Hill, Chapel Hill, NC, United States
1Biomedical Engineering, UNC Chapel Hill, Chapel Hill, NC, United States, 2Department of Radiology and Biomedical Research Imaging Center (BRIC), UNC Chapel Hill, Chapel Hill, NC, United States
Synopsis
We evaluated the effectiveness of optimal-shrinkage singular value decomposition (OS-SVD) in denoising multi-channel complex-valued diffusion MRI data prior to image reconstruction and show that it outperforms other state-of-the-art denoising methods.
Introduction
In MRI, increasing spatial resolution is met with increasing noise level. The accompanying decrease in signal-to-noise ratio eventually causes structural details to be overwhelmed by noise, countering the benefits of increased spatial resolution. In this work, we evaluated the effectiveness of optimal-shrinkage singular value decomposition (OS-SVD) [1] in reducing noise from multi-channel complex-valued diffusion data.Methods
Optimal shrinkage of singular valuesDiffusion MRI data are redundant. Information across coil channels, volumes of different diffusion gradients, and neighboring voxels is not entirely independent but shares some degree of similarity. This redundancy is manifested via the low-rank nature of the matrix formed by signals from channels, volumes, and neighboring voxels. However, in practice the matrix is full-rank due to noise. Noise-free data can be recovered by estimating a low-rank matrix from the full-rank matrix. For this purpose, we employ OS-SVD with nuclear norm as the loss function to preserve structural information [1].
Denoising pipeline
We propose a 4-stage process for OS-SVD denoising:
Channel decorrelation and denoising – Noise is correlated across coil channels. We perform whitening transformation using the covariance matrix computed across channels with signals acquired without excitation to decorrelate noise.
Background phase estimation and phase unwinding – Physiological factors such as brain motion, cardiac pulsation, perfusion and respiration can cause back- ground phase variations [2]. The background phase is estimated by OS-SVD denoising of the real and imaginary parts separately. The phase of the complex data is then unwound via subtraction with the estimated background phase [2].
Shrinkage of singular values – After phase unwinding, the imaginary part, con- taining only noise, is discarded. OS-SVD is performed on the real part with a sliding 5-by-5-by-5 block to recover the noise-free signal.
Phase rewinding – The phase is rewound by adding back the background phase.
Results
Evaluation was performed using dMRI data acquired using single-band acquisition at 1 mm isotropic resolution with a total of 65 volumes covering 64 gradient directions with b = 500, 1000, 2000, 3000 s mm−2 and a B0 image. We compare OS-SVD with MP-PCA implemented as ‘dwidenoise’ in Mrtrix3 [3] and magnitude-based shrinkage with variance stabilization transform ‘VST-Mag’ as described in [4].Effects on DWIs
Fig. 1 shows the diffusion-weighted images with different b-values for the original noisy data and after denoising by dwidenoise, VST-Mag, and OS-SVD. OS-SVD removes noise effectively, especially at high b-value.
Effects on Microstructural Indices
We evaluated the effects of denoising on microstructural indices estimated from various models, including DTI [5], NODDI [6], and SMSI [7]. From Fig. 2, OS-SVD yields a markedly cleaner DTI FA map compared with the noisy data and the dwidenoise data. VST-Mag result is overly smoothed, losing structural details. The effects of noise on SMSI microscopic FA (μFA) is less severe because SMSI is based on the spherical mean. OS-SVD gives reasonable NODDI intra-cellular volume fractions vIC unlike the competing methods.
Effects on Orientation Estimation and Tractography
We employed MSMT-CSD [8] to estimate the fiber orientation distribution function (fODF) and global tractography [9] to estimate whole-brain tractograms. From Fig. 3 indicates that OS-SVD yields cleaner fODFs and tractogram compared with the dwidenoise and VST-Mag.
Conclusions
We have shown that optimal shrinkage of singular values is an effective means of reducing noise in multi-channel complex-valued diffusion MRI data, outperforming state-of-the-art methods in yielding improved diffusion-weighted images, microstructural indices, and tractograms.Acknowledgements
This work was supported in part by NIH grant NS093842.References
- Gavish, M., Donoho, D.L.: Optimal shrinkage of singular values. IEEE Transactions on Information Theory 63(4) (2017) 2137–2152
- Eichner, C., Cauley, S.F., Cohen-Adad, J., Mo ̈ller, H.E., Turner, R., Setsompop, K., Wald, L.L.: Real diffusion-weighted mri enabling true signal averaging and increased diffusion contrast. NeuroImage 122 (2015) 373–384
- Veraart,J.,Fieremans,E.,Novikov,D.S.:Diffusionmrinoisemappingusingrandom matrix theory. Magnetic resonance in medicine 76(5) (2016) 1582–1593
- Ma, X., Ug ̆urbil, K., Wu, X.: Denoise magnitude diffusion magnetic resonance images via variance-stabilizing transformation and optimal singular-value manipu- lation. NeuroImage (2020) 116852
- Veraart, J., Sijbers, J., Sunaert, S., Leemans, A., Jeurissen, B.: Weighted linear least squares estimation of diffusion mri parameters: strengths, limitations, and pitfalls. NeuroImage 81 (2013) 335–346
- Daducci, A., Canales-Rodr ́ıguez, E.J., Zhang, H., Dyrby, T.B., Alexander, D.C., Thiran, J.P.: Accelerated microstructure imaging via convex optimization (amico) from diffusion mri data. NeuroImage 105 (2015) 32–44
- Huynh, K.M., Xu, T., Wu, Y., Wang, X., Chen, G., Wu, H., Thung, K., Lin, W., Shen, D., Yap, P.: Probing tissue microarchitecture of the baby brain via spherical mean spectrum imaging. IEEE Transactions on Medical Imaging (2020) 1–1
- Jeurissen, B., Tournier, J.D., Dhollander, T., Connelly, A., Sijbers, J.: Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion mri data. NeuroImage 103 (2014) 411–426
- Christiaens, D., Reisert, M., Dhollander, T., Sunaert, S., Suetens, P., Maes, F.: Global tractography of multi-shell diffusion-weighted imaging data using a multi- tissue model. Neuroimage 123 (2015) 89–101
Figures
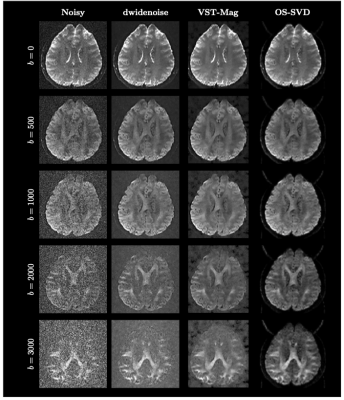
Fig. 1. Effects on Diffusion-Weighted Images. Images for different b-values from the the original noisy dataset and after denoising with dwidenoise, VST-Mag, and OS-SVD.
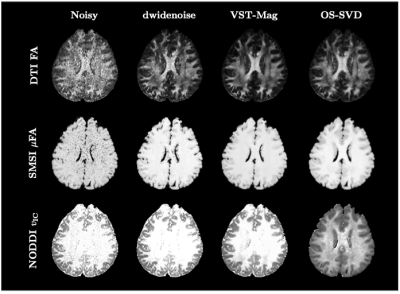
Fig. 2. Effects on microstructural indices. DTI FA, SMSI μFA, and NODDI $$$v_\text{IC}$$$ .
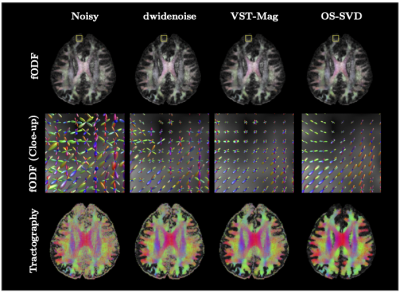
Fig.3. Effects on Orientation Estimation and Tractography. OS-SVD improves estimation of the fiber orientation distribution function (fODF) and eventually tractography.