2465
The diffusion time dependence of MAP-MRI parameters in the human brain1Eunice Kennedy Shriver National Institute of Child Health and Human Development, National Institutes of Health, Bethesda, MD, United States, 2Center for Neuroscience and Regenerative Medicine, The Henry Jackson Foundation, Bethesda, MD, United States, 3Athinoula A. Martinos Center for Biomedical Imaging, Department of Radiology, Massachusetts General Hospital, Harvard Medical School, Charlestown, MA, United States, 4Harvard-MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, MA, United States
Synopsis
We acquire mean apparent propagator (MAP) MRI data in the human brain using different diffusion times. We characterize the diffusion-time dependence of propagator metrics in vivo and compute the statistical distance between co-registered propagators measured with short and long diffusion times. We derive time-scaling parameters that can assess anomalous diffusion in disordered, fractal-like tissue environments. Preliminary results suggest that the diffusion-time dependence of in vivo MRI signals is strongly modulated by restrictions and hindrances that occur over a range of length scales and could provide new contrasts to quantify structural and architectural differences in healthy and diseased tissues.
Introduction
The average diffusion propagator describes the spatial and temporal evolution of water diffusion over multiple length and time scales. Mean apparent propagator (MAP) MRI1 is a comprehensive and clinically feasible2 method for assessing tissue microstructure. From measurements with multiple b-values and gradient orientations, but a fixed diffusion time, MAP-MRI explicitly measures the net 3D displacements of water molecules. Studies have shown that the self-similarity of neuronal cells across multiple length scales can be viewed as fractal-like structures4. Brownian motion in such microenvironments gives rise to anomalous diffusion5. Temporal scaling (TS) MRI6 models anomalous diffusion in disordered, fractal-like media and leads to the diffusion-time dependent scaling behavior of two important MAP-MRI–derived metrics, the mean-squared displacement (MSD), and the return-to-origin probability (RTOP).In this study, we quantify whole-brain MAPs at different diffusion times in vivo. From the MAP-derived MSD and RTOP, we compute TS-MRI parameters to assess morphological features derived from the anomalous diffusion process. Measuring the time evolution of diffusion propagators can improve our ability to quantify tissue morphological features characterizing cell shape, size, or density and may yield sensitive, clinically relevant biomarkers for assessing changes that occur in many neurodegenerative diseases.
Methods
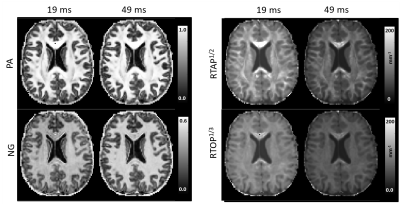
We conducted whole-brain MAP-MRI scans in a healthy volunteer using the Connectome scanner7. Specifically, we acquired MAP-MRI datasets with short diffusion time Δ=19ms, bmax=6000s/mm2 and 434 DWIs, and long diffusion time Δ=49ms, bmax=17800s/mm2 and 466 DWIs, respectively. The gradient pulse duration for both scans was δ=8ms. All DWIs had a 2mm isotropic spatial resolution, a 21.6cm field-of-view, TE=77ms, TR=4000ms, SMS=2, GRAPPA=2. We processed8 all DWIs to correct for subject motion, magnetic susceptibility, and eddy current distortions and analyzed the short and long diffusion time datasets with MAP-MRI.We assessed the diffusion time dependence of propagator metrics: return-to-origin (RTOP), return-to-axis (RTAP), and return-to-plane probabilities (RTPP), propagator anisotropy (PA), and non-gaussianity (NG), as well as fiber orientation displacement profiles (fODFs). We quantified the statistical distance between co-registered propagators (i.e., probability density functions of spin displacements) measured with short and long Δ, using a metric derived from information theory called the Jensen-Shannon Divergence (JSD)9.
Moreover, we estimated the random walk dimension, dw, and the spectral dimension, ds, which describe the temporal scaling of the MSD, $$$\left< r^2\right>$$$, and RTOP parameters derived from propagators measured with different diffusion times: $$$\left< r^2\right>\propto{t^{\frac{2}{d_w}}}$$$, and, $$$RTOP\propto{t^{-\frac{d_s}{2}}}$$$, respectively. From these two dynamic exponents we computed the fractal dimension $$$d_f=\frac{d_{s}d_w}{2}$$$, an important parameter that describes the scaling of the mass of a fractal-like environment with distance.
Results
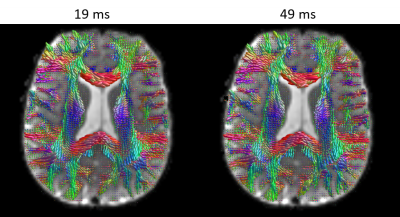
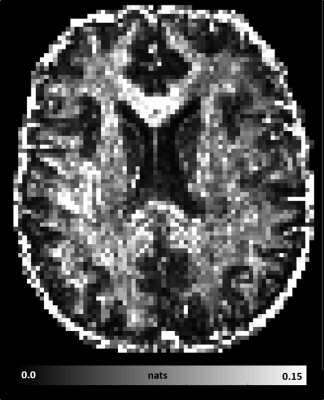
MAP-MRI parameters measured with short and long diffusion times showed significant differences in both gray matter (GM) and white matter (WM) (Fig. 1). Specifically, zero-displacement probabilities such as RTOP, RTAP, or RTPP decreased by approximately 30-50% when measured with Δ=49ms compared to Δ=19ms, with the larger percent differences observed in GM. The PA increased slightly in WM (<5%) but decreased in GM (<10%) at long diffusion time. The NG increased in WM (~10%) but decreased in GM (~8%). Fiber orientation distribution functions (fODFs) were relatively unaffected by the diffusion time of our experiment (Fig. 2). This consistency of the preferred diffusion directions suggests that the diffusion time dependence of the MRI measurement may not significantly affect MAP-MRI applications such as fiber tractography or connectivity mapping.The JSD measure highlights regions where the increase in diffusion time alters the orientation and shape of the normalized distributions of water molecule net displacements (Fig. 3). The highest JSD values were observed in regions with compact WM pathways, such as the corpus callosum, where water diffusion is more restricted. Such restrictions may occur over a range of length scales giving rise to anomalous diffusion in fractal-like structures which can be quantified using the TS-MRI parameters dw, ds, and df. We found evidence of sub-diffusion ($$$d_w>2$$$) throughout the brain, with slightly higher dw in WM compared to GM, suggesting that the distances traveled by water molecules scale slower than linearly with time as in Gaussian diffusion. The spectral dimension, ds, showed a clearer distinction between GM and WM, with higher values in GM, while df was relatively constant across brain tissues.
Discussion
Our preliminary results show that propagator metrics depend on diffusion time and that this dependence can be measured in healthy volunteers in a clinically feasible scan or acquisition time. The lack of changes in fODFs along with the changes in RTAP, RTOP, PA, and NG suggest that microstructural restrictions and hindrances play important roles in the diffusion of tissue water.In idealized experiments, for example, when using diffusion phantoms containing impermeable pores and sufficiently long diffusion times, the zero-displacement probabilities (e.g., RTAP and RTOP) can be inversely related to the average pore size (e.g., cross-sectional area or volume, respectively). The time-dependence of these parameters observed in our study suggests that in tissues diffusion is affected by restrictions and hindrances over multiple length scales. Such a process can give rise to anomalous diffusion in fractal-like media, which can be efficiently described with TS-MRI, whose parameters may be sensitive to different cell types. This work represents an important step towards the clinical translation of TS-MRI and improves our understanding of the diffusion-time dependence10-14 of in vivo MRI signals.
Acknowledgements
This work was supported by the NIH BRAIN Initiative grant U01-EB-026996, the Intramural Research Program (IRP) of the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD) and the Center for Neuroscience and Regenerative Medicine (CNRM) under the auspices of the Henry Jackson Foundation (HJF).References
1. Özarslan, E. et al. Mean apparent propagator (MAP) MRI: A novel diffusion imaging method for mapping tissue microstructure. NeuroImage 78, 16-32, doi:10.1016/j.neuroimage.2013.04.016 (2013).
2. Avram, A. V. et al. Clinical feasibility of using mean apparent propagator (MAP) MRI to characterize brain tissue microstructure. NeuroImage 127, 422-434, doi:10.1016/j.neuroimage.2015.11.027 (2016).
3. Lichtman, J. W. & Denk, W. The big and the small: challenges of imaging the brain’s circuits. Science 334, 618-623 (2011).
4. Smith Jr, T., Marks, W., Lange, G., Sheriff Jr, W. & Neale, E. A fractal analysis of cell images. Journal of neuroscience methods 27, 173-180 (1989).
5. Gefen, Y., Aharony, A. & Alexander, S. Anomalous diffusion on percolating clusters. Physical Review Letters 50, 77 (1983).
6. Özarslan, E. et al. Observation of anomalous diffusion in excised tissue by characterizing the diffusion-time dependence of the MR signal. Journal of Magnetic Resonance 183, 315-323, doi:10.1016/j.jmr.2006.08.009 (2006).
7. Huang, S. Y. et al. High-gradient diffusion MRI reveals distinct estimates of axon diameter index within different white matter tracts in the in vivo human brain. Brain Structure and Function 225, 1277-1291 (2020).
8. Jenkinson, M., Beckmann, C. F., Behrens, T. E., Woolrich, M. W. & Smith, S. M. Fsl. Neuroimage 62, 782-790 (2012).
9. Lin, J. Divergence measures based on the Shannon entropy. IEEE Transactions on Information theory 37, 145-151 (1991).
10. Latour, L. L., Svoboda, K., Mitra, P. P. & Sotak, C. H. Time-dependent diffusion of water in a biological model system. Proceedings of the National Academy of Sciences 91, 1229-1233 (1994).
11. Pfeuffer, J., Flögel, U., Dreher, W. & Leibfritz, D. Restricted diffusion and exchange of intracellular water: theoretical modelling and diffusion time dependence of 1H NMR measurements on perfused glial cells. NMR in Biomedicine: An International Journal Devoted to the Development and Application of Magnetic Resonance In Vivo 11, 19-31 (1998).
12. Sen, P. N. Time‐dependent diffusion coefficient as a probe of geometry. Concepts in Magnetic Resonance Part A: An Educational Journal 23, 1-21 (2004).
13. Novikov, D. S., Fieremans, E., Jensen, J. H. & Helpern, J. A. Random walks with barriers. Nature physics 7, 508 (2011).
14. Novikov, D. S., Jensen, J. H., Helpern, J. A. & Fieremans, E. Revealing mesoscopic structural universality with diffusion. Proceedings of the National Academy of Sciences of the United States of America 111, 5088-5093, doi:10.1073/pnas.1316944111 (2014).
Figures