2464
Towards more robust and reproducible Diffusion Kurtosis Imaging1Champalimaud Research, Champalimaud Centre for the Unknown, Lisbon, Portugal, 2Department of Clinical Medicine, Aarhus University, Aarhus, Denmark, 3Department of Physics and Astronomy, Aarhus University, Aarhus, Denmark, 4School of Psychology, Cardiff University, Cardiff, United Kingdom, 5Mary MacKillop Institute for Health Research, Australian Catholic University, Melbourne, Australia, 6Center for Biomedical Imaging, NYU Grossman School of Medicine, New York, NY, United States
Synopsis
The general utility of Diffusion Kurtosis Imaging (DKI) is challenged by its poor robustness to imaging artifacts and thermal noise that often lead to implausible kurtosis values. A robust scalar kurtosis index can be estimated from powder-averaged diffusion-weighted data. We introduce a novel DKI estimator that uses this scalar kurtosis index as a proxy for the mean kurtosis to regularize the fit. The regularized DKI estimator improves the robustness and reproducibility of the kurtosis metrics and results in parameter maps with enhanced quality and contrast; thereby promoting the wider use of DKI in clinical research and potentially diagnostics.
Introduction
Despite a growing interest in biophysical models to develop specific biomarkers of microstructural changes, diffusion tensor imaging (DTI; [1]) or diffusion kurtosis tensor imaging (DKI; [2]) retain the potential to become invaluable tools in diagnostic and clinical research. DTI and DKI provide metrics that are highly sensitive to microstructural changes associated with development, aging, disease and disorder without adopting (often contested) model assumptions. Given the availability of accelerated image acquisition techniques, data compatible with whole-brain DKI-analysis can be acquired in a few of minutes, thereby facilitating clinical utility. Moreover, recent large cohort studies, e.g. the HCP [3], UK Biobank [4], ADNI [5], and CamCAN [6] provide large-scale multishell data that are well-suited to DKI analyses. Unfortunately, DKI has been challenged by a poor robustness to imaging artifacts and thermal noise that often leads to non-physical kurtosis values [7]. Indeed, implausible negative values are ubiquitous in many kurtosis maps, hampering visual, quantitative, and statistical analysis of the data. Advances in artifact correction, noise removal, and constrained parameter estimation [7] have reduced, but not eliminated the problem [8]. We propose and evaluate a novel technique for more robust and precise estimation of the full kurtosis tensor - this is based on a regularized DKI estimator in which the estimated mean kurtosis is evaluated against a robust prediction of the mean kurtosis.Methods
Powder kurtosis: A scalar kurtosis quantity can be obtained from diffusion-weighted signals averaged across different isotropically-distributed gradient directions (and for each individual $$$b$$$-value): the powder kurtosis $$$\mathring{K}$$$ [9,10]. The powder kurtosis is overall a good and robust proxy for the mean kurtosis $$$\bar{K}$$$. However, there is a significant difference between both metrics that is proportional with anisotropy of the diffusion tensor.Robust prediction of the mean kurtosis: A mean kurtosis prediction $$$\hat{K}$$$ can be obtained from $$$\mathring{K}$$$ and the diffusion tensor D using a polynomial regression model without the need for estimating the full kurtosis tensor. The thousands of non-problematic voxels within each data set, i.e. positive apparent kurtosis in each direction, serve as training data. In this strategy, voxel quality transfer, the polynomial coefficients are estimated using multivariate polynomial regression prior to applying the model to the problematic voxels.
Robust DKI fitting: The prediction of the mean kurtosis from the powder-averaged data is a much more robust and reproducible metric than $$$\bar{K}$$$ estimated from the fitted kurtosis tensor (see results). Therefore, we hypothesize the $$$\| \bar{K} - \hat{K}\|^2_2$$$ regularizes the nonlinear least squares estimation of the DKI tensor.
Diffusion MRI Data: A test-retest reproducibility analysis with $$$N=5$$$ subjects is performed using a multi-shell diffusion protocol: b = 0 (4 repetitions), b = 500, b = 1000, and b = 2500 $$$s/mm^2$$$ (30 directions each). The echo time was 66ms and the voxel size was 2.5mm isotropic.
Results
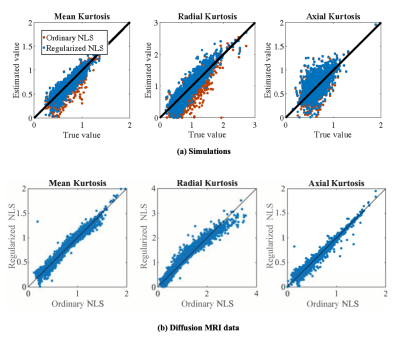
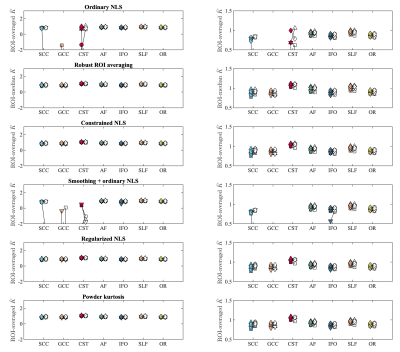
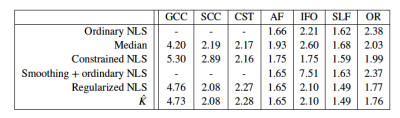
Accuracy of regularized tensor fitting: Figure 1(a) summarizes simulation results by showing the ground truth reference of DKI parameters versus their estimates obtained using the ordinary and regularized NLS estimator. The average percentage difference between the estimated and ground truth mean kurtosis is -6.57 and -1.59% for the ordinary and regularized NLS estimators. For the radial kurtosis $$$K_\perp$$$, the average percentage difference decreases from -16.65 to -7.82% when regularizing the tensor fitting. For axial kurtosis $$$K_\parallel$$$, the percentage difference is minimally altered: 4.58 and 5.86%.In Figure 1(b), we show the correspondence between estimated kurtosis parameters using the ordinary and regularized NLS estimator in non-problematic test voxels in which the ordinary NLS serves as gold standard. The average percentage difference between the ordinary and regularized NLS estimators for $$$\bar{K}$$$, $$$K_\perp$$$, and $$$K_\parallel$$$ is 0.64%, 0.62%, and -0.40%, respectively.Reproducibility: Figure 2 shows the mean $$$\bar{K}$$$ within each ROI as computed in 5 subjects using various fitting strategies for the test and retest data. The test/retest reproducibility is typically poor when using ordinary NLS estimators, with and without spatial smoothing, because in at least one of the scans the negative kurtosis outliers dominate the ROI-averaged $$$\bar{K}$$$. The median operator is robust to such outliers and can be used as a reference target for reproducibility analysis. The test/retest reproducibility is greatly improved by the use of the regularized fitting algorithm. The Test/retest variability of the ROI-averaged metrics is tabulated in Table 1.
General applicability: In Figure 3 we show the maps of $$$\bar{K}$$$ for various openly available datasets (HCP, ADNI, and CamCAN) using the ordinary and regularized NLS.
Discussion and Conclusion
The mean kurtosis can be very well predicted without the need to estimate the kurtosis tensor using a polynomial regression model that can be trained on the hundreds of thousands of non-problematic voxels in the same or similar data sets. By doing so, one transfers the excellent quality of the DKI estimation in the majority of the voxels to the few, yet persistently problematic voxels. The accurate and robust prediction of the mean kurtosis might be relevant and sufficient for various studies. However, the regularized fitting is a necessary additional step for all studies that have interest in directional kurtosis, DKI-derived biophysical modeling [11], or tractography [12].Acknowledgements
Research was performed as part of the Center of Advanced Imaging Innovation and Research (CAI2R, www.cai2r.net), an NIBIB Biomedical Technology Resource Center (NIH P41 EB017183) and was partially supported by the NINDS of the NIH (R01 NS088040). The Connectom data were acquired at the UK National Facility for in vivo MR Imaging of Human Tissue Microstructure funded by the EPSRC (grant EP/M029778/1), and The Wolfson Foundation. DKJ is supported by a Wellcome Trust Investigator Award (096646/Z/11/Z) and a Wellcome Trust Strategic Award (104943/Z/14/Z).References
[1] Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophys J 1994; 66(1): 259-67
[2] Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional kurtosis imaging: the quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magn. Reson. Med. 2005; 53(6): 1432–1440.
[3] Van Essen DC, Smith SM, Barch DM, et al. The WU-Minn Human Connectome Project: An overview. NeuroImage 2013;80: 62–79.
[4] Miller KL, Alfaro-Almagro F, Bangerter NK, et al. Multimodal population brain imaging in the UK Biobank prospective epidemiological study. Nature Neuroscience 2016; 19(11): 1523–1536.
[5] Weiner MW, Veitch DP, Aisen PS, et al. The Alzheimer’s Disease Neuroimaging Initiative: A review of papers published since its inception. Alzheimers Dement 2012; 8: 1–68.
[6] Taylor JR, Williams N, Cusack R, et al. The Cambridge Centre for Ageing and Neuroscience (Cam-CAN) data repository:Structural and functional MRI, MEG, and cognitive data from a cross-sectional adult lifespan sample. NeuroImage 2017;144: 262–269.
[7] Tabesh A, Jensen JH, Ardekani BA, Helpern JA. Estimation of tensors and tensor-derived measures in diffusional kurtosis imaging. Magnetic resonance in medicine 2011; 65(3): 823–836.
[8] Ades-Aron B, Veraart J, Kochunov P, et al. Evaluation of the accuracy and precision of the diffusion parameter EStImation with Gibbs and NoisE removal pipeline. NeuroImage 2018; 183: 532–543
[9] Lasic, S, Szczepankiewicz F, Eriksson S, Nilsson M, Topgaard D. Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic-angle spinning of the q-vector. Frontiersin Physics 2014; 2: 11.
[10] Price D, Tyler LK, Henriques RN, et al. Age-related delay in visual and auditory evoked responses is mediated by white and grey-matter differences. Nature Communications 2017; 8(1): 15671.
[11] Fieremans E, Jensen JH, Helpern JA. White matter characterization with diffusional kurtosis imaging. Neuroimage 2011;58(1): 177–188.
[12] Glenn GR, Helpern JA, Tabesh A, Jensen JH. Quantitative assessment of diffusional kurtosis anisotropy. NMR inBiomedicine 2015; 28(4): 448–459.
Figures