2459

Tissue microstructure by ellipsoidal tensor encoding with independently varying spectral anisotropy and tuning

Samo Lasic^1,2 and Henrik Lundell¹
¹Danish Research Centre for Magnetic Resonance, Centre for Functional and Diagnostic Imaging and Research, Copenhagen University Hospital Hvidovre, Copenhagen, Denmark, ²Random Walk Imaging, Lund, Sweden

Synopsis

Ellipsoidal tensor encoding (ETE) with independent control of spectral anisotropy (SA) and tuning provides two distinct encoding frequency windows in a single experiment and yields distinctly different signal signatures for compartments with different anisotropic time-dependent diffusion. ETE can be orientation invariant, depending on SA and restriction geometry. Signal orientation variation minima depends on size relative to tuning but not on orientation dispersion. This popery could be useful for quick size estimation and geometry detection. Such encoding strategy could potentially provide new contrasts sensitive to specific pathological variations.

INTRODUCTION

Tensor-valued diffusion encoding can probe diffusion tensor distributions unconfounded by the orientation distribution^1-10. This can be achieved by employing b-tensors of varying shapes. Effects of time-dependent diffusion (TDD) in tensor-valued encoding have not yet been fully studied. We have been exploring two new encoding dimensions: spectral anisotropy (SA) and tuning of b-tensors. SA^11,12 provides orientation dependent sensitivity to TDD and can explain the break down of rotational invariance for spherical b-tensors^12-14. For orientationally averaged signals, tuning affects mean diffusivity^12,15 while SA affects attenuation at higher b-values.

Here we propose an alternative encoding scheme employing ellipsoidal tensor encoding (ETE) with independent control of SA and tuning. Instead of varying tuning (diffusion times), like e.g. in experiments employing oscillating gradients^16-18, we explore the possibility of varying SA at constant tuning. This approach provides two distinct encoding frequency windows in a single experiment and yields distinctly different signal signatures for compartments with different anisotropic TDD. Furthermore, a minimum of signal variation can be found by tuning and depends on restriction size but not on orientation dispersion. These unique experimental features could provide new contrasts sensitive to specific pathological variations.

METHODS

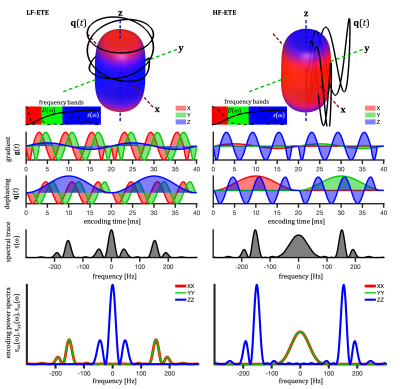
We evaluate the first-order effect of SA, i.e. assuming mono-exponential signal decay for each compartment. This assumption is reasonable when the effects of the intra-compartmental kurtosis are less prominent^14,19.

TDD can in the first-order be evaluated based on the cross power spectral density, defined in terms of the Fourier transforms of dephasing waveforms $$$\mathbf{q}(t)$$$ (see Fig. 1), $$s_{ij}(\omega) \equiv q_i(\omega)\bar{q}_j(\omega).$$ The total encoding power (b-tensor), is given by $$ b_{ij}=\frac{1}{2\pi}\int_{-\infty}^{\infty}s_{ij}(\omega)d\omega$$ and the b-value is determined by the spectral trace $$$s(\omega) \equiv \sum_{i=1}^{3} s_{ii}(\omega)$$$¹².

Single compartment attenuation factor is given by $$\beta \equiv -\ln{S/S_0} = \sum_{i,j,k} R_{ki}R_{kj} \Lambda_{ijk},$$ where $$$R_{ij}$$$ are rotation matrix elements. To evaluate $$\Lambda_{ijk} \equiv \frac{1}{b} \frac{1}{2\pi} \int_{-\infty}^{\infty} s_{ij}(\omega) \lambda_k(\omega) d\omega,$$
we consider diffusion restricted in simple geometries^12,16.

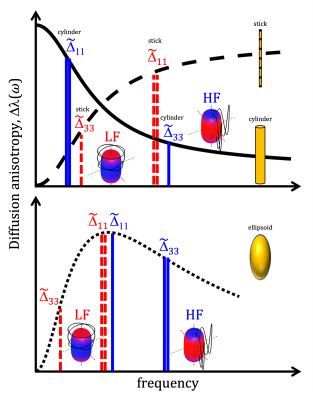
For axisymmetric compartments with $$$\lambda_1(\omega) = \lambda_2(\omega)\neq \lambda_3(\omega)$$$, and $$ \Delta\lambda(\omega)\equiv \lambda_3(\omega) - \lambda_1(\omega),$$ the apparent diffusion anisotropy is reflected in $$\Delta_{ij} \equiv \Lambda_{ij3} - \Lambda_{ij1}.$$ To explicitly accounts for waveform shapes, we can consider the normalized spectra $$$\tilde{s}_{ij}(\omega) \equiv \frac{1}{b_{ij}} s_{ij}(\omega)$$$ with the factorization $$$\Delta_{ij} \equiv \frac{b_{ij}}{b} \tilde{\Delta}_{ij}$$$, where $$ \tilde{\Delta}_{ij} = \frac{1}{2\pi} \int_{-\infty}^{\infty} \tilde{s}_{ij}(\omega) \Delta\lambda(\omega) d\omega.$$ For free diffusion, $$$\tilde{\Delta}_{ij}$$$ is independent of waveform shape and $$$\Delta_{ij}$$$ depends only on b-tensor anisotropy and not on SA.

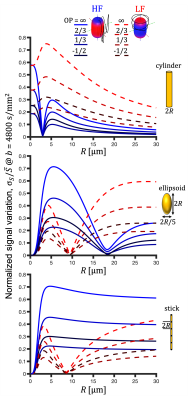
Cylindrical, ellipsoidal and stick-like restrictions with zero radial and restricted axial diffusion were considered^12,16. Prolate ellipsoidal restrictions (5:1 axes ratio) were approximated by $$$D(\omega)$$$ for spheres of different sizes. Signals were calculated for the prolate ellipsoidal tensor encoding (ETE) with $$$b_{33}/b_{11}=2$$$, $$$b\leq 4800\, \mathrm{s/mm^2}$$$ and for 15 uniform encoding directions. Watson orientation distributions were considered with order parameters (OP)^5,6 of -0.5, 0, 1/3, 2/3 and 1 (Watson $$$\kappa$$$ of -$$$\infty$$$, 2.24, 5.28 and $$$\infty$$$). Color coded spectral anisotropy shown in Fig. 1 was obtained from projections of the power spectra¹²(see caption of Fig. 1).

RESULTS AND DISCUSSION

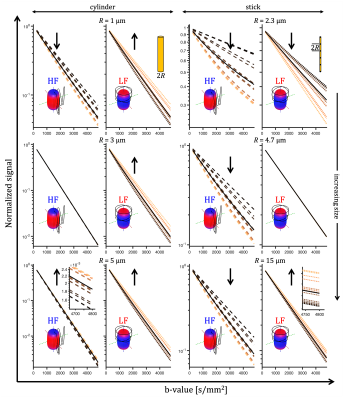
For a single compartment and axisymmetric encoding, $$$b_{11}=b_{22}\neq b_{33}$$$, attenuation factors span a range given by $$\Delta\beta = b[\Delta_{33}-\Delta_{11}] = b_{33}\tilde{\Delta}_{33}-b_{11}\tilde{\Delta}_{11}.$$ $$$\Delta\beta = 0$$$ when $$\frac{b_{33}}{b_{11}} \frac{\tilde{\Delta}_{33}}{\tilde{\Delta}_{11}} = 1.$$ For prolate or oblate b-tensors, the effect of anisotropy can vanish when $$$\tilde{\Delta}_{11}>\tilde{\Delta}_{33}$$$ or $$$\tilde{\Delta}_{33}>\tilde{\Delta}_{11}$$$, respectively, in which case encoding can become rotationally invariant. The invariance condition for our prolate ETE with more power at high frequencies (HF-ETE) or low frequencies (LF-ETE) along the long axis and for different geometries is illustrated in Fig. 2. For ellipsoidal restrictions, $$$\Delta\lambda(\omega)$$$ has a maximum which depends on restriction shape and size. Consequently, $$$\Delta\beta$$$ can be positive or negative regardless of the ratio $$$b_{33}/b_{11}$$$. This is reflected in the signal variation minima shown in Fig. 3. The minima for the normalized signal variation (Fig. 3) occur only with HF-ETE for cylinders or with LF-ETE for sticks, while for ellipsoidal restrictions we have minima with both encodings.

The critical sizes or tuning yielding minimal signal variation depend on geometry but not on orientation dispersion. As illustrated in Fig. 4, when switching between HF-ETE and LF-ETE, $$$\Delta\beta$$$ can change sign, i.e. yields a reversed order of attenuations from different directions. This can occur for cylinders or sticks below or above the critical size, respectively, a feature which could allow for quick size and geometry detection.

CONCLUSION

The ability to independently control tuning and spectral anisotropy in ETE could be useful for quick size estimation and geometry detection. Such encoding strategy could potentially be valuable to discriminate between different morphologies in heterogeneous systems, which might yield similar responses with more conventional approaches. A closer examination of conditions best suited for the suggested encoding, comparisons with more conventional approaches, gradient optimization strategies and the limitations will be subject of future work.

Acknowledgements

This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 804746). SL is also supported by Random Walk Imaging.

References

1. S. Eriksson, S. Lasič, and D. Topgaard, Isotropic diffusion weighting in PGSE NMR by magic- angle spinning of the q-vector., Journal of Magnetic Resonance 226, 13 (2013).

2. S. Lasič, F. Szczepankiewicz, S. Eriksson, M. Nilsson, and D. Topgaard, Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic-angle spinning of the q-vector, Frontiers in Physics 2, 1 (2014).

3. F. Szczepankiewicz, S. Lasič, D. van Westen, P. C. Sundgren, E. Englund, C.-F. Westin, F. Ståhlberg, J. Lätt, D. Topgaard, and M. Nilsson, Quantification of microscopic diffusion anisotropy disentangles effects of orientation dispersion from microstructure: applications in healthy volunteers and in brain tumors., NeuroImage 104, 241 (2015).

4. C.-F. Westin, H. Knutsson, O. Pasternak, F. Szczepankiewicz, M. Kubicki, D. Topgaard, and M. Nilsson, Q-space trajectory imaging for multidimensional diffusion MRI of the human brain, Neuroimage, 135, 345 (2016).

5. D. Topgaard, Multidimensional diffusion MRI, Journal of Magnetic Resonance 275, 98 (2017).

6. D. Topgaard, NMR methods for studying microscopic diffusion anisotropy, in Diffusion NMR of confined systems: fluid transport in porous solids and heterogeneous materials, New Developments in NMR no. 9, edited by R. Valiullin (Royal Society of Chemistry, Cambridge, UK,2017).

7. F. Szczepankiewicz, D. van Westen, E. Englund, C. F. Westin, F. Ståhlberg, J. Lätt, P. C.Sundgren, and M. Nilsson, The link between diffusion MRI and tumor heterogeneity: Mapping cell eccentricity and density by diffusional variance decomposition (DIVIDE), NeuroImage 142, 522 (2016).

8. D. Topgaard, Diffusion tensor distribution imaging, NMR in Biomedicine 32, 1 (2019).

9. M. Nilsson, F. Szczepankiewicz, J. Brabec, M. Taylor, C. F. Westin, A. Golby, D. van Westen, and P. C. Sundgren, Tensor-valued diffusion MRI in under 3 minutes: an initial survey of 15 microscopic anisotropy and tissue heterogeneity in intracranial tumors, Magnetic Resonancein Medicine 83, 608 (2020), arXiv:1902.09986.

10. J. P. de Almeida Martins, C. M. Tax, A. Reymbaut, F. Szczepankiewicz, M. Chamberland, D. K. Jones, and D. Topgaard, Computing and visualising intra-voxel orientation-specific relaxation–diffusion features in the human brain, Human Brain Mapping , 1 (2020).

11. H. Lundell, M. Nilsson, C.-F. Westin, D. Topgaard, and S. Lasič, Spectral anisotropy in multidimensional diffusion encoding, in Proc. Intl. Soc. Mag. Reson. Med. 26 (2018) p. 0887.

12. H. Lundell and S. Lasič, Diffusion encoding with general gradient waveforms, in Advanced Diffusion Encoding Methods in MRI: New Developments in NMR Volume 24, edited by D. Topgaard (Royal Society of Chemistry, Cambridge, UK, 2020).

13. T. M. De Swiet and P. P. Mitra, Possible Systematic Errors in Single-Shot Measurements of the Trace of the Diffusion Tensor, Journal of Magnetic Resonance, Series B 111, 15 (1996).

14. S. N. Jespersen, J. L. Olesen, A. Ianu ̧s, and N. Shemesh, Effects of nongaussian diffusion on “isotropic diffusion” measurements: An ex-vivo microimaging and simulation study, Journal of Magnetic Resonance 300, 84 (2019).

15. H. Lundell, M. Nilsson, T. B. Dyrby, G. J. Parker, P. L. Cristinacce, F. L. Zhou, D. Topgaard, and S. Lasič, Multidimensional diffusion MRI with spectrally modulated gradients reveals unprecedented microstructural detail, Scientific Reports 9, 1 (2019).

16. J. Stepišnik, Time-dependent self-diffusion by NMR spin-echo, Physica B 183, 343 (1993).

17. J. C. Gore, J. Xu, D. C. Colvin, T. E. Yankeelov, E. C. Parsons, and M. D. Does, Characterization of tissue structure at varying length scales using temporal diffusion spectroscopy, NMR in Biomedicine 23, 745 (2010).

18. H. Lundell, C. K. Sønderby, and T. B. Dyrby, Diffusion weighted imaging with circularly polarized oscillating gradients, Magnetic Resonance in Medicine 73, 1171 (2015).

19. R. N. Henriques, S. N. Jespersen, and N. Shemesh, Correlation tensor magnetic resonance imaging, NeuroImage 211, 116605 (2020), arXiv:1908.00122.

Figures

Figure 1: Tuned ellipsoidal tensor encodings with varying spectral anisotropy featuring more encoding power at low frequencies (LF-ETE) or high frequencies (HF-ETE) along z-axis. While the trace spectra is similar for LF-ETE and HF-ETE, the power distribution across different directions is markedly different. Color coding is based on the RGB-weights given by projections of the encoding power in the three bands with crossover frequencies determined by $$$D(\omega)$$$ for a sphere with $$$D_0^2R^{-4}=8000 \,\mathrm{s}^{-2}$$$ reaching 1/3 and 2/3 of the asymptotic value.

Figure 2: Interplay between b-tensor shape and spectral anisotropy. Diffusion anisotropy, $$$\Delta\lambda(\omega)$$$, monotonically decreases or increases with frequency for cylindrical or stick-like restrictions, while it is non-monotonic for ellipsoidal pores. In prolate ETE, the effect of anisotropy can vanish when $$$\tilde{\Delta}_{11}>\tilde{\Delta}_{33}$$$, which is possible for cylinders with HF-ETE or sticks with LF-ETE. For ellipsoidal pores, the above condition can be fulfilled with both encodings depending on tuning relative to restriction size.

Figure 3: Directional spread of signals (normalized STD, $$$\sigma_\mathrm{S}/\bar{S}$$$) as a function of compartment size for cylindrical, ellipsoidal and stick-like restrictions. HF-ETE (solid blue lines) and LF-ETE (dashed red lines) for Watson orientation distributions with varying order parameters (OP). Location of the minima is independent of OP. For cylindrical restrictions, the minima occur only with the HF-ETE, while for stick-like restrictions, the minima occur only with the LF-ETE. For ellipsoidal restrictions we have minima with both LF-ETE and HF-ETE.

Figure 4: Normalized signal attenuations for cylindrical and stick-like restrictions for HF-ETE and LF-ETE (alternating columns) for selected restriction sizes (see Fig. 3) and 15 directions (dark to bright). At a critical size, attenuations become directionally invariant for cylinders measured with HF-ETE and sticks with LF-ETE. For cylinders/sticks below/above the critical size, switching between HF-ETE and LF-ETE yields a reversed order of attenuations from different directions. This feature could be useful for estimation of size and restriction geometry.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

2459