2458
Gradient waveforms for comprehensive sampling of the frequency and "shape" dimensions in b(Ω)-encoded diffusion MRI1Physical Chemistry, Lund University, Lund, Sweden
Synopsis
Diffusion encoding with either oscillating gradients or as a function of the "shape" of the b-tensor have both recently found powerful applications for characterization of tissue microstructure in clinical MRI. We here propose a simple scheme based on the "double rotation" technique in solid-state NMR spectroscopy to generate a family of gradient waveforms enabling comprehensive sampling of the multidimensional space defined by the tensor-valued encoding spectrum with special emphasis on the frequency and shape dimensions. The approach is demonstrated by microimaging experiments on phantoms with well-defined anisotropy and restriction properties, thereby paving the way for future clinical implementations.
Introduction
Diffusion MRI methods with advanced gradient modulation schemes have recently been shown to have great potential for clinical applications1 - a few notable examples being oscillating gradients to estimate cell sizes in breast tumors2 and "tensor-valued" encoding for detecting white matter in cortical malformations related to epilepsy3. The sensitivity of the MRI signal to various aspect of diffusion can be quantified with the tensor-valued encoding spectrum b(ω)4,5, the trace of which equals the dephasing power spectrum6 – often denoted |F(ω)|2 – relevant for isotropic restricted diffusion7, and whose integral over ω equals the conventional b-matrix8 giving information about diffusion anisotropy.While most studies focus on either the frequency9 or tensorial10 aspects of the encoding, Lundell et al.11 recently suggested joining the frequency and tensor "shape"12 dimensions into a common multidimensional framework. The approach was demonstrated with gradient waveforms deriving from the magic-angle spinning (MAS) technique in solid-state NMR spectroscopy13-15, which, however, offer only limited accessibility to the frequency and shape dimensions. Expanding on these previous results, we here take inspiration from the "double rotation" (DOR) technique in solid-state NMR16 and derive a family of gradient waveforms for comprehensive exploration of, in particular, the frequency-shape space of b(ω). The new waveforms are demonstrated by measurements on phantoms with well-defined diffusion properties using microimaging equipment.
Methods
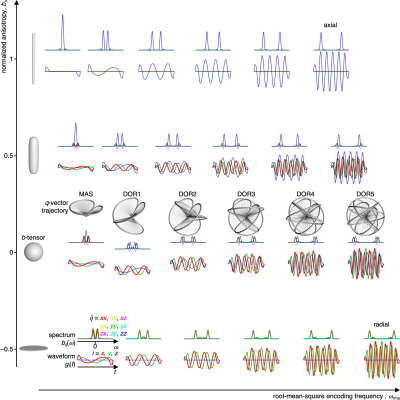
DOR unit vector trajectories were calculated by subjecting the vector [0, 0, 1]T to a series of rotations (from right to left) Rz(Ψ2)Ry(ζ2)Rz(Ψ1)Ry(ζ1), where ζ1 = π/2 and ζ2 = acos(1/31/2) are the inclinations of the two rotation axes. The time-dependent angles of rotation Ψ1 and Ψ2 about the two axes are coupled by the relation Ψ1 = nΨ2, where n is an integer and Ψ2 increases from 0 to 2π during the time t from 0 to τ. The unit vector trajectories were converted to q-vector trajectories and gradient waveforms gi(t) as described in detail previously17. We note that the unit vector trajectories may be written explicitly using reasonably compact expressions with trigonometric functions, illustrating that the trajectories derive from simple geometric considerations.A three-compartment phantom was prepared by inserting a 4 mm NMR tube with saturated magnesium nitrate and a 4 mm NMR tube with lamellar liquid crystal into a 10 mm NMR tube with MilliQ water. The sediment of yeast cells was prepared as in Eriksson et al.14
MRI was performed on a Bruker Neo 500 MHz spectrometer equipped with an 11.7 T magnet and a MIC-5 microimaging probe capable of delivering 3 T/m gradients on-axis. Images were acquired with spin-echo prepared single-shot RARE at 0.6×0.6 mm2 in-plane spatial resolution, 1 mm slice thickness, and 16×16×1 matrix size. Diffusion encoding employed pairs of identical gradient waveforms bracketing the 180º pulse in the preparation block18. Data was acquired for 8 b-values up to 6.44×109 sm–2 and 15 orientations for each of the 24 waveforms in figure 1 using constant waveform duration τ = 25 ms and maximum gradient amplitude 3 T/m.
Results & Discussion
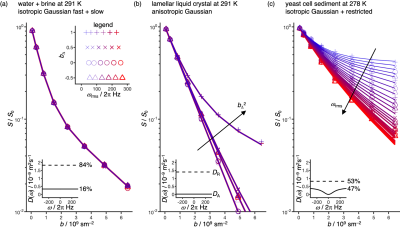
Figure 1 shows the herein used gradient waveforms gi(t) and corresponding encoding spectra bij(ω) placed in a 2D space of root-mean-square encoding frequency ωrms, being controlled by the value of n, and the tensor “shape” bΔ parameter12, adjusted by scaling the axial and radial components of the gradient waveforms19. The waveforms are scaled to give identical b-values and rotated to align the cylindrical symmetry axis of the encoding tensor with the gradient frame z-direction. The q-vector trajectories, labeled DORn with n = 1, 2, …, 5 and MAS, are displayed for the cases with bΔ = 0 to illustrate the reasonably simple geometries underlying the waveforms. The axial and radial waveforms resemble, respectively, the cosine-modulated oscillating gradients of Parsons et al.20 and the circularly polarized version introduced by Lundell et al21.Experimental data are displayed in Figure 2. The collapse of all data onto a single master curve signal-vs.-b for the isotropic Gaussian phantom verifies that all 24 waveforms for sampling the 2D (ωrms, bΔ) space give the same b-values. For the anisotropic Gaussian phantom, the signal is independent of ωrms but depends strongly on bΔ and can be well fitted by the “Pake” expression valid for randomly oriented axisymmetric diffusion tensors12. Conversely, for the restricted phantom the signal depends strongly on ωrms consistent with the diffusion spectrum D(ω) for spherical confinement22.
Conclusions and Outlook
The proposed family of gradient waveforms enables comprehensive sampling of both the frequency and shape dimensions of diffusion encoding as required for detailed characterization of restrictions and anisotropy in heterogeneous materials such as brain tissues. The present waveforms, deriving from simple geometrical considerations, are suitable for pre-clinical investigations of small animals on high-gradient systems. By numerical optimizations to maximize the b-value for given gradient strength15,23, mitigating image artifacts from eddy currents24 and concomitant gradients25, and further minimizing side-lobes in the encoding spectra26, we foresee that the waveforms may be adapted for human in vivo studies. The merging of oscillating gradients9 and tensor-valued encoding10 into a common acquisition protocol encourages the development of a joint analysis framework, for instance by augmenting current nonparametric diffusion tensor distributions27 with a frequency dimension building on the concept of confinement tensors28.Acknowledgements
This work was financially supported the Swedish Foundation for Strategic Research (ITM17-0267), Swedish Research Council (2018-03697), and Chinese Scholarship Council. DT owns shares in Random Walk Imaging AB (Lund, Sweden, http://www.rwi.se/), holding patents related to the described methods.References
1. Reymbaut A, Zheng Y, Li S, Sun W, Xu H, Daimiel Naranjo I, Thakur S, Pinker-Domenig K, Rajan S, Vanugopal VK, Mahajan V, Mahajan H, Critchley J, Durighel G, Sughrue M, Bryskhe K, Topgaard D. Clinical research with advanced diffusion encoding methods in MRI. In: Topgaard D, (Ed.). Advanced Diffusion Encoding Methods in MRI. Cambridge, UK: Royal Society of Chemistry; 2020. p 406-429. doi: 10.1039/9781788019910-00406
2. Xu J, Jiang X, Li H, Arlinghaus LR, McKinley ET, Devan SP, Hardy BM, Xie J, Kang H, Chakravarthy AB, Gore JC. Magnetic resonance imaging of mean cell size in human breast tumors. Magn Reson Med 2020;83:2002-2014. doi: 10.1002/mrm.28056
3. Lampinen B, Zampeli A, Björkman-Burtscher IM, Szczepankiewicz F, Kallen K, Compagno Strandberg M, Nilsson M. Tensor-valued diffusion MRI differentiates cortex and white matter in malformations of cortical development associated with epilepsy. Epilepsia 2020. doi: 10.1111/epi.16605
4. Topgaard D. Multiple dimensions for random walks. J Magn Reson 2019;306:150-154. doi: 10.1016/j.jmr.2019.07.024
5. Lundell H, Lasič S. Diffusion encoding with general gradient waveforms. In: Topgaard D, (Ed.). Advanced Diffusion Encoding Methods in MRI. Cambridge, UK: Royal Society of Chemistry; 2020. p 12-67. doi: 10.1039/9781788019910-00012
6. Stepišnik J. Analysis of NMR self-diffusion measurements by a density matrix calculation. Physica B 1981;104:305-364. doi: 10.1016/0378-4363(81)90182-0
7. Callaghan PT, Stepišnik J. Frequency-domain analysis of spin motion using modulated-gradient NMR. J Magn Reson A 1995;117:118-122. doi: 10.1006/jmra.1995.9959
8. Mattiello J, Basser PJ, LeBihan D. Analytical expressions for the b matrix in NMR diffusion imaging and spectroscopy. J Magn Reson A 1994;108:131-141. doi: 10.1006/jmra.1994.1103
9. Aggarwal M. Restricted diffusion and spectral content of the gradient waveforms. In: Topgaard D, (Ed.). Advanced Diffusion Encoding Methods in MRI, New Developments in NMR. Cambridge, UK: Royal Society of Chemistry; 2020. p 103 - 122. doi: 10.1039/9781788019910-00103
10. Reymbaut A. Diffusion anisotropy and tensor-valued encoding. In: Topgaard D, (Ed.). Advanced Diffusion Encoding Methods in MRI, New Developments in NMR. Cambridge, UK: Royal Society of Chemistry; 2020. p 68 - 102. doi: 10.1039/9781788019910-00068
11. Lundell H, Nilsson M, Dyrby TB, Parker GJM, Cristinacce PLH, Zhou FL, Topgaard D, Lasič S. Multidimensional diffusion MRI with spectrally modulated gradients reveals unprecedented microstructural detail. Sci Rep 2019;9:9026. doi: 10.1038/s41598-019-45235-7
12. Eriksson S, Lasič S, Nilsson M, Westin C-F, Topgaard D. NMR diffusion encoding with axial symmetry and variable anisotropy: Distinguishing between prolate and oblate microscopic diffusion tensors with unknown orientation distribution. J Chem Phys 2015;142:104201. doi: 10.1063/1.4913502
13. Andrew ER, Bradbury A, Eades RG. Removal of dipolar broadening of nuclear magnetic resonance spectra of solids by specimen rotation. Nature 1959;183:1802-1803. doi: 10.1038/1831802a0
14. Eriksson S, Lasič S, Topgaard D. Isotropic diffusion weighting by magic-angle spinning of the q-vector in PGSE NMR. J Magn Reson 2013;226:13-18. doi: 10.1016/j.jmr.2012.10.015
15. Topgaard D. Isotropic diffusion weighting in PGSE NMR: Numerical optimization of the q-MAS PGSE sequence. Microporous Mesoporous Mater 2013;178:60-63. doi: 10.1016/j.micromeso.2013.03.009
16. Samoson A, Lippmaa E, Pines A. High resolution solid-state NMR: Averaging of second-order effects by means of a double-rotor. Mol Phys 1998;65:1013-1018. doi: 10.1080/00268978800101571
17. Topgaard D. Multidimensional diffusion MRI. J Magn Reson 2017;275:98-113. doi: 10.1016/j.jmr.2016.12.007
18. Lasič S, Szczepankiewicz F, Eriksson S, Nilsson M, Topgaard D. Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic-angle spinning of the q-vector. Front Physics 2014;2:11.
19. Topgaard D. Director orientations in lyotropic liquid crystals: Diffusion MRI mapping of the Saupe order tensor. Phys Chem Chem Phys 2016;18:8545-8553. doi: 10.1039/c5cp07251d
20. Parsons EC, Does MD, Gore JC. Modified oscillating gradient pulses for direct sampling of the diffusion spectrum suitable for imaging sequences. Magn Reson Imaging 2003;21:279-285.
21. Lundell H, Sønderby CK, Dyrby TB. Diffusion weighted imaging with circularly polarized oscillating gradients. Magn Reson Med 2015;73:1171-1176. doi: 10.1002/mrm.25211
22. Stepišnik J. Time-dependent self-diffusion by NMR spin-echo. Physica B 1993;183:343-350. doi: 10.1016/0921-4526(93)90124-O
23. Sjölund J, Szczepankiewicz F, Nilsson M, Topgaard D, Westin C-F, Knutsson H. Constrained optimization of gradient waveforms for generalized diffusion encoding. J Magn Reson 2015;261:157-168. doi: 10.1016/j.jmr.2015.10.012
24. Yang G, McNab JA. Eddy current nulled constrained optimization of isotropic diffusion encoding gradient waveforms. Magn Reson Med 2019;81:1818-1832. doi: 10.1002/mrm.27539
25. Szczepankiewicz F, Westin CF, Nilsson M. Maxwell-compensated design of asymmetric gradient waveforms for tensor-valued diffusion encoding. Magn Reson Med 2019;82:1424-1437. doi: 10.1002/mrm.27828
26. Hennel F, Michael ES, Pruessmann KP. Improved gradient waveforms for oscillating gradient spin-echo (OGSE) diffusion tensor imaging. NMR Biomed 2020:e4434. doi: 10.1002/nbm.4434
27. Topgaard D. Diffusion tensor distribution imaging. NMR Biomed 2019;32:e4066. doi: 10.1002/nbm.4066
28. Yolcu C, Memic M, Simsek K, Westin CF, Özarslan E. NMR signal for particles diffusing under potentials: From path integrals and numerical methods to a model of diffusion anisotropy. Phys Rev E 2016;93:052602. doi: 10.1103/PhysRevE.93.052602
29. Kindlmann G. Superquadric tensor glyphs. In: Deussen O, Hansen C, Keim DA, Saupe D, (Eds.). Proceedings IEEE TVCG/EG Symposium on Visualization: Eurographics Association Aire-la-Ville, Switzerland; 2004. p 147-154. doi: 10.2312/VisSym/VisSym04/147-154
Figures