Introduction

Diffusion weighted imaging (DWI) is a widely used non-contrast technique that probes the thermally driven displacement of water molecules. For a traditional spin echo implementation, the diffusion encoding gradient waveforms are designed using two symmetric trapezoidal (TRAP) gradients on either side of the 180-degree refocusing pulse. More advanced implementations using symmetric gradient design have also been proposed to meet constraints such as a motion compensation with gradient moment nulling for liver or cardiac DWI^1,2.
Recently, asymmetric gradient waveform design, with a varying number of gradients before and after the refocusing pulse, have been shown to afford better b-value performance than symmetric designs³. In general, asymmetric gradient waveform design is performed by numerical optimization^3-6 and can meet a variety of constraints, such as motion compensation, eddy current compensation⁷, Maxwell compensation⁸ or to reduce peripheral nerve stimulation (PNS). These numerical optimizations generate arbitrary (ARB) shaped gradient waveforms, which are not-necessarily TRAP in shape. For practical reasons, these ARB shapes may be approximated as a set of TRAP waveforms. However, this approximation trades-off precision relative to the design constraints. ARB gradient waveforms can be complicated to implement, but offer several advantages over TRAP gradients. In symmetric design, ARB gradient waveforms offer advantages relative to TRAP designs, including maximizing the diffusion sensitivity to microscruture^9,10 and limiting PNS without de-rating slew rate limit on the gradient system¹¹.
The first objective of this work was to analyze the eddy current and motion compensation performances of asymmetric numerical designs, before and after converting them from ARB to TRAP waveforms. The second objective was to analyze the benefit for b-value and PNS of an ARB ramp-up gradient over TRAP gradient for traditional symmetric analytical designs.

Methods

All the diffusion encoding waveforms were designed in silico for a fixed DWI protocol (FOV=300x300mm², matrix=128x128, GRAPPA 2x, slice thickness=5mm, BW=2056Hz/px, b-value =500s/mm², 6 diffusion directions, TE=90ms, TR=1000ms). The hardware (3T Prisma, Siemens Healthineers) was rated at Gmax=80mT/m, SR_max=200mT/m/s derated to SR_limit=50mT/m/s for PNS purposes. The waveforms were described by the moments gradient:
$$M_n=\int_{0}^{TE}G(t).t^n.dt$$
where M₀≈0 is required for imaging while a nulled first (M₁=0) and/or second (M₁=M₂=0) moment offers velocity and acceleration compensation, respectively.

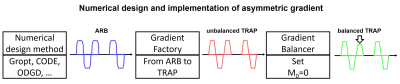
For the first objective, the performance of ARB and TRAP gradients were compared for asymmetric gradient waveforms design. Waveforms were generated numerically using the GrOpt toolbox5, wihich produces ARB waveforms that can be converted to TRAP (Fig. 1). Owing to digitization errors, the resulting set of TRAPs need to be balanced to ensure a strict M₀=0 by changing the gradient amplitude of one of the TRAPs. ARB waveforms with motion compensation (M₁=M₂=0) and with eddy current nulling (single nulled eddy current constant λ=20ms) were generated and compared before and after being converted to TRAP waveforms. For analysis, a full eddy current spectrum ranging from λ=0 to λ=200ms was used.

For the second objective, the ARB and TRAP symmetric gradient waveforms were studied in terms of b-value and PNS. To avoid PNS stimulation, gradient waveforms are usually strongly slew rate limited, which limits the maximum achievable b-value for a given gradient amplitude and duration. An ARB waveform that maximizes b-value and avoid PNS can be designed by using a cubic polynomial ramp-up with one degree of freedom:
$$G_{RampUp}(t)=G_{Max}(1-exp(a.t+a^2.t^2+a^3.t^3))$$
where a is parameter that can be analytically selected to maximize the slew rate and limit PNS. Here, symmetric TRAP waveforms were designed analytically with SR_max=200mT/m/s and SR_limit=50mT/m/s were compared to the ARB waveforms in terms of b-value and PNS limit.

Results

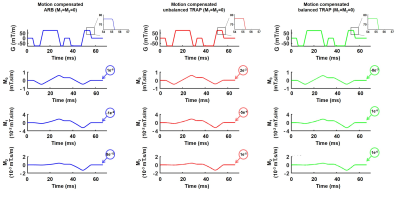
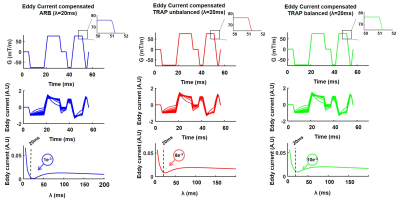
An example of motion compensated ARB waveforms (M₁=M₂=0) designed numerically with GrOpt is given in Figure 2. The ARB waveforms were then converted to TRAPs and balanced. This conversion increased the zero, first and second order gradient moments. The ARB waveform design had M0=1x10^-6mT•s/m, which increases after TRAP conversion to M0=2.4x10^-2mT•s/m, but can be reduced by two orders of magnitude after balancing the TRAPs (M0=-7.8x10^-5mT•s/m). The motion compensation constraint was met for the ARB waveforms (M1=-1x10^-9mT•s²/m, M2=-7.9x10^-13mT•s³/m), but significantly increased after conversion (M1=5x10^-4mT•s²/m, M2=1.2x10^-5mT•s³/m) and balancing (M₁=1.1x10^-5mT•s²/m, M₂=1.2x10^-6mT•s³/m). For comparison, a monopolar waveform with the same timing would resulted in M₀=1.7x10^-14mT•s/m, M₁=-4.4x10^-2mT•s²/m and M₂=-2.7x10^-3mT•s³/m.

The eddy current ARB waveform numerically designed (Figure 3) reduces the eddy current magnitude over the full range of the spectrum and remains essentially the same for unbalanced and balanced TRAP waveforms. When the waveform is designed to mitigate eddy currents using λ=20ms, the resulting eddy current magnitude was 1x10^-3 for ARB, 8x10^-3 for the unbalanced TRAP, and 10x10^-3 for the balanced TRAP. For comparison, a monopolar waveform would have an eddy current magnitude of 27 at λ=20ms.

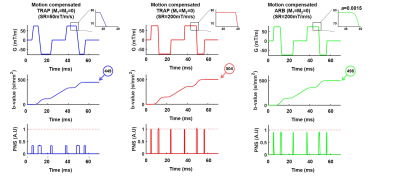
Finally, symmetric motion compensated waveforms (M₁=M₂=0) with SRmax and SRlimit were compared to an ARB cubic ramped waveforms (a=1.5x10^-3) in Figure 4. The b-value of the TRAP waveforms with SRmax (b-value=504s/mm²) can be nearly matched by the ARB (b-value=496s/mm²) while avoiding PNS stimulation (PNS<1).

Discussions and Conclusion

Despite a more complex implementation, ARB waveforms can meet precise design constraints defined in the numerical optimization while their conversion to TRAP waveform is usually at a cost of performance. ARB waveforms are also valuable in analytical symmetric designs to optimize the b-value while managing PNS.