2454
Improved parameter estimation for non-Gaussian IVIM using an unbiased vector non-local means
Lyu Jian1,2, Xinyuan Zhang1,2,3, Yingjie Mei4, and Li Guo1,2,5
1School of Biomedical Engineering, Southern Medical University, Guangzhou, China, 2Guangdong Provincial Key Laboratory of Medical Image Processing, Southern Medical University, Guangzhou, China, 3Guangdong-Hong Kong-Macao Greater Bay Area Center for Brain Science and Brain-Inspired Intelligence, Guangzhou, China, 4Philips Healthcare, Guangzhou, China, 5Department of MRI, The First People’s Hospital of Foshan (Affiliated Foshan Hospital of Sun Yat-sen University), Foshan, China
1School of Biomedical Engineering, Southern Medical University, Guangzhou, China, 2Guangdong Provincial Key Laboratory of Medical Image Processing, Southern Medical University, Guangzhou, China, 3Guangdong-Hong Kong-Macao Greater Bay Area Center for Brain Science and Brain-Inspired Intelligence, Guangzhou, China, 4Philips Healthcare, Guangzhou, China, 5Department of MRI, The First People’s Hospital of Foshan (Affiliated Foshan Hospital of Sun Yat-sen University), Foshan, China
Synopsis
Non-Gaussian intravoxel incoherent motion (NG-IVIM) has been proposed to simultaneously quantify the perfusion and non-Gaussian diffusion properties in tissues. However, accurate parameter estimation for NG-IVIM is usually challenged by noise. The noncentral χ-distribution noise would introduce bias in the estimated NG-IVIM parameters. In addition, severe noise easily causes the estimated parameter values have large variance. To improve the accuracy and precision of parameter estimation for NG-IVIM, we propose to use an unbiased vector non-local means (UVNLM) filter to denoise and correct the noise bias before NG-IVIM model fitting.
Introduction
Non-Gaussian intravoxel incoherent motion (NG-IVIM)1 has been proposed to simultaneously quantify the perfusion and non-Gaussian diffusion properties in tissues. However, accurate parameter estimation for NG-IVIM is usually challenged by noise. The noncentral χ-distribution noise would introduce bias in the estimated NG-IVIM parameters. In addition, severe noise easily causes the estimated parameter values have large variance. To improve the accuracy and precision of parameter estimation for NG-IVIM, we propose to use an unbiased vector non-local means (UVNLM) filter to denoise and correct the noise bias before NG-IVIM model fitting.Methods
UVNLM subtracts the noise bias from the vector NLM (VNLM)2 filtered image, which can be expressed as:$$UVNLM(m(x_{i}))=\sqrt{(VNLM(m(x_{i})))^{2}-2L\sigma^{2}}$$(1)where L is the number of coil channels, σ is the standard deviation (SD) of noncentral χ-distribution noise, m(xi) is a vector of size Ndwi indicating the signal profile at position xi in image m, NDWI is the total number of non-diffusion and diffusion images. VNLM(m(xi)) is a spatial domain filter2 that replaces each signal vector m(xi) in the image with a weighted average of every neighboring signal vector m(xj) in its “search region” Vi:$$VNLM(m(x_{i}))=\sum_{x_{j}\in V_{i}}w(x_{i},x_{j})m(x_{j})$$(2)
w(xi,xj) is the weight that controls the contribution of neighboring pixel xj within search window to the target pixel xi and is defined as:$$w(x_{i},x_{j})=\frac{1}{Z(x_{i})}exp(-\frac{G_{a}||P(x_{i})-P(x_{j})||_2^2}{h^{2}}),\forall x_{j}\in V_{i} and x_{j} \neq x_{i}$$(3)
with$${Z(x_{i})}=\sum_{x_{j}\in V_{i}}exp(-\frac{G_{a}||P(x_{i})-P(x_{j})||_2^2}{h^{2}})$$(4)
where Z(xi) is the normalized constant, Ga a normalized Gaussian kernel (the SD of a), h controls the degree of smoothing and determined as h = βσ, where β is a scalar. P(xi) and P(xj) denote 3D patch of p×p×NDWI, where p is the patch size in the spatial domain, and the patch size along the diffusion dimension is set to NDWI. To avoid the over-weighting due to the self-similarity when xj = xi, the weight w(xi, xi) is calculated as w(xi, xi) = max{w(xi, xj), $$$\forall$$$xj≠xi}. With the UVNLM, the parameters of NG-IVIM model can be estimated by using the following objective function:$$\min_{\theta}\sum_{n=1}^{N_{DWI}}\|UVNLM(S_{m}(b_{n}))-S(b_{n};{\theta})||_{2}^{2}$$(5)
where Sm is the measured signal profile of a single pixel, bn the diffusion weighting strength of nth diffusion weighted image, θ = {f, D*, Dapp, Kapp, S0} the NG-IVIM model parameter, S the noise-free diffusion signal which can be written as follows:$$S(b;\theta)=S_{0}(fexp(-bD^{*})+(1-f)exp(-bD_{app}+\frac{(bD_{app})^{2}K_{app}}{6}))$$(6)
where S0 is the signal without diffusion gradient (b = 0), f the perfusion fraction, D* the pseudodiffusion coefficient related to the blood flow velocity, Dapp the apparent diffusion coefficient, Kapp the apparent kurtosis.
Simulations were performed based on a synthetic liver NG-IVIM data. The liver parenchyma parameters of f = 0.15, D* = 50 ×10-3 mm2/s, Dapp = 1.5×10-3 mm2/s, and Kapp = 0.8 were used to simulate the reference NG-IVIM data with 18 b-values of 0, 10, 20, 30, 40, 60, 80, 100, 150, 200, 300, 400, 500, 600, 800, 1000, 1500, 2000 s/mm2. The reference images were then used to generate noncentral Chi (L = 8) distributed serial images with three SNRs of 10, 30, 50.
We compared the following three methods: 1) conventional nonlinear least squares (NLS) without denoising and bias correction; 2) NLS after principal component analysis denoising (referred as PCA-NLS); 3) NLS after UVNLM (referred as UVNLM-NLS).
Results
Fig. 1 presents the RMSEs of NG-IVIM maps estimated by the different methods. The proposed UVNLM-NLS method outperformed the conventional NLS and PCA-NLS for D*, Dapp, Kapp at all three SNRs. In Figs. 2-4, a visual comparison of the estimated NG-IVIM maps and their corresponding error maps is presented for conventional NLS (Fig. 2), PCA-NLS (Fig. 3), and the proposed UVNLM-NLS (Fig. 4). It can be seen that the parameter maps from the proposed method were visually closest to the reference parameter maps among all compared methods under three SNRs of 10, 30, 50.Discussion and conclusion
In order to reduce the noise effect on the NG-IVIM parameter estimation, we adopted a UVNLM scheme to reduce both the noise variance and bias on the image domain before the model fitting. Simulation results demonstrated that the UVNLM scheme can significantly improve parameter estimation for NG-IVIM. Our future work would be to validate the usefulness of UVNLM scheme for improving parameter estimation of NG-IVIM on clinical in vivo data.Acknowledgements
This study was funded by China Postdoctoral Science Foundation (NO.2020M672526), Guangdong Basic and Applied Basic Research Foundation (NO.2019A1515110976), National Natural Science Foundation of China (NO.61971214, 81601564), Natural Science Foundation of Guangdong Province (NO.2019A1515011513), Guangdong-Hong Kong-Macao Greater Bay Area Center for Brain Science and Brain-Inspired Intelligence Fund (NO.2019022).References
[1] Lu YG, et al. “Extension of the Intravoxel Incoherent Motion Model to Non-Gaussian Diffusion in Head and Neck Cancer’’. J Magn Reson Imag 36: 1088-1096 (2012). [2] Wiest-Daessl´e N, et al. “Non-Local Means Variants for Denoising of Diffusion-Weighted and Diffusion Tensor MRI”. Med Image Comput Comput Assist Interv 10: 344–351. PMID: 18044587. (2007)Figures
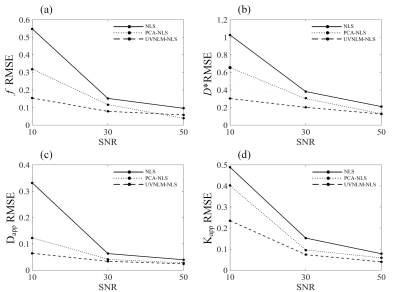
Fig. 1. RMSE comparisons
of f, D*, Dapp, Kapp
maps estimated with the conventional NLS, the PCA-NLS, the proposed UVNLM-NLS
method.
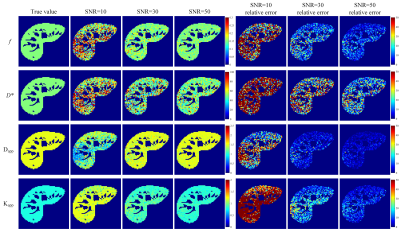
Fig.
2. f, D*, Dapp, Kapp maps and their corresponding
error maps of the conventional NLS method. The error maps show the absolute
difference between the reference parameters and the estimated parameters.

Fig.
3. f, D*, Dapp, Kapp maps and their corresponding
error maps of the PCA-NLS method. The error maps show the absolute difference
between the reference parameters and the estimated parameters.
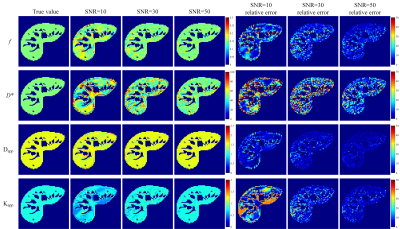
Fig.
4. f, D*, Dapp, Kapp maps and their corresponding
error maps of the proposed UVNLM-NLS method. The error maps show the absolute
difference between the reference parameters and the estimated parameters.