2449

Patch-CNN-DTI: Data-efficient high-fidelity tensor recovery from 6 direction diffusion weighted imaging.

Tobias Goodwin-Allcock¹, Ting Gong¹, Robert Gray², Parashkev Nachev², and Hui Zhang¹
¹Centre for Medical Image Computing (CMIC), UCL, London, United Kingdom, ²High-Dimensional Neurology, University College London Queen Square Institute of Neurology, London, United Kingdom

Synopsis

We present Patch-CNN-DTI, a deep-learning method to estimate diffusion tensors (DT) accurately from only 6 diffusion-weighted images. Early voxel-wise deep-learning methods can only estimate scalar measures of DT. Later work shows DT can be estimated using image-wise methods based on convolutional neural networks (CNN), but they require large training cohort. Patch-CNN-DTI can estimate DT with only one training subject, by pooling information from local neighbourhood of a voxel similar to the CNN but at a much smaller scale to minimise training data requirements. Results show it outperforms conventional model fitting with twice the number of diffusion directions.

Introduction

This work aims to produce a deep-learning technique to estimate accurate diffusion tensors (DT) with a minimal number of diffusion weighted images (DWI) and training subjects. Diffusion tensor imaging (DTI) allows us to examine white matter (WM) microstructure and connectivity non-invasively. However, 30 DWIs are required to estimate DT accurately¹ which is not always practical for time-sensitive diseases, such as stroke. Recently, deep-learning has been proposed to reduce the number of DWIs required. The DiffNet² algorithm showed that scalar measures of DT, including mean diffusivity (MD) and fractional anisotropy (FA), can be estimated with high accuracy from just 6 DWIs. It estimates these quantities using a simple voxel-wise architecture that requires only a few training subjects. However, it does not estimate the primary diffusion direction required for tractography. DeepDTI³ shows the entire DT can be estimated with as few DWIs. However, it uses a more complex, image-wise, convolutional architecture, requiring an order of magnitude more subjects to train. Here we present an approach that can estimate the DT, like DeepDTI, but having a minimal training-data requirement, like DiffNet.

Methods

Model Design: Training data requirements are minimised by adopting H-CNN⁴, a deep-learning model designed to leverage local neighbourhood information but at a minimal level. Similar to DiffNet, the input consists of 7 channels: b=0 and 6 b=1000 DWIs and the model consists of several fully-connected layers. Unlike DiffNet, a convolutional layer replaces the first fully-connected layer to pool information from the input layer across a small patch of 3x3x3. And the output layer has 6 channels to support the DT estimation for the central voxel of each patch. To ensure estimated DTs are positive-definite, the model outputs the matrix-log of DTs, its 6 independent components; corresponding DTs can be estimated by matrix-exponentiation.

Evaluation: To assess the proposed method, DWI data from the Human Connectome Project⁵ (HCP) is used, as it has a large set of DTI-compatible measurements that can provide 1) a high-quality ‘ground-truth’ DTs using conventional fitting; 2) DWI subsets with fewer measurements. The full set of DTI-compatible measurements include b=0’s (18) and b=1000’s (90) which are all used to fit the ‘ground truth’ (GT) diffusion tensors. A single b=0 image and an optimal subset⁶ of 6 b=1000’s are chosen as in DeepDTI to test the proposed method. Its performance is evaluated against conventional fitting and a DiffNet-like model (Voxel-NN) applied to the same 6-DWI subset. For benchmarking, conventional fitting is additionally applied to optimal 12 and 30-DWI subsets. Conventional fitting is performed with FSL⁷. The matrix logarithm of DTs is computed using MATLAB after ensuring DTs are positive-definite.

The proposed Patch-CNN model and the Voxel-NN model are trained with a single HCP subject, using the optimal 6-DWI subset as input and the ‘ground-truth’ DTs as output. Training settings follow the implementation of H-CNN: a batch size of 256; optimisation uses ADAM⁸ optimiser; the learning rate is set to 0.001 initially and subsequently reduced by 50% at each plateau. To reduce overfitting, early stopping is applied with a random choice of 20% of the brain voxels as validation, with the remaining 80% for training.

The trained model is applied to 4 unseen HCP subjects and the errors between estimated and GT measurements are assessed over the whole brain using the frobenius norm for tensors; the absolute difference for FA and MD. To assess its ability to reconstruct WM bundles, the angular errors between the estimated primary diffusion directions and the ones from GT tensors are computed over the WM.

Results

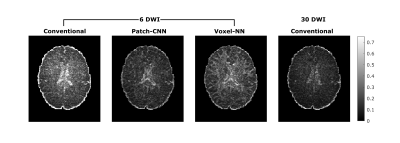
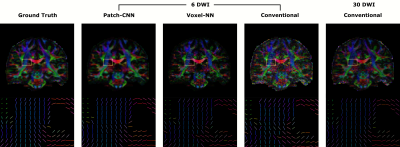
Figure 1 shows qualitatively Patch-CNN estimates DTs more accurately than Voxel-NN and conventional fitting with 6 DWIs. Figure 4a confirms this quantitatively and additionally shows that Patch-CNN outperforms conventional fitting with twice as many DWIs.

Figure 2 shows primary diffusion directions Patch-CNN estimates are also more accurate than those from Voxel-NN and conventional fitting with 6 DWIs. Figure 4b confirms this and again shows that Patch-CNN outperforms conventional fitting with twice as many DWIs.

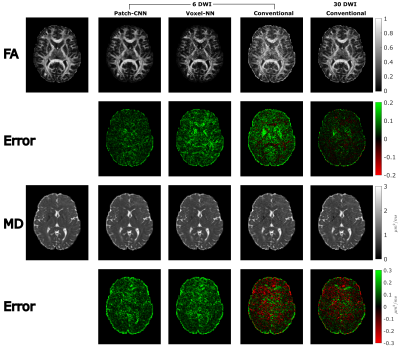
Finally, Figure 3 shows MD and FA can be estimated more accurately with Patch-CNN than Voxel-NN and conventional fitting with 6-DWIs. Figures 4c and 4d again confirm that Patch-CNN outperforms conventional fitting with twice as many DWIs.

It has been suggested that 30 DWIs is required to perform robust fitting¹, therefore, we compared Patch-CNN against 30 DWI conventional fitting. For estimation of MD Patch-CNN performs marginally better than 30 DWI conventional fitting, for the other parameters performance is only slightly worse.

Discussion and Conclusion

Patch-CNN has been demonstrated to outperform conventional fitting for estimating the DT and the clinically useful measures derived from it, matching the performance of conventional fitting with twice the number of DWIs. Patch-CNN achieves this performance with only one training subject which is a vast improvement from image-wise CNNs, such as DeepDTI which requires around 40 training subjects as well as both T1w and T2w anatomical images. Patch-CNN makes tractography available for time-sensitive diseases. Further work is to validate the performance of this technique on tractography and apply it to real clinical datasets.

Acknowledgements

No acknowledgement found.

References

[1] D. K. Jones, ‘The effect of gradient sampling schemes on measures derived from diffusion tensor MRI: A Monte Carlo study’, Magn. Reson. Med., vol. 51, no. 4, pp. 807–815, 2004.

[2] E. Aliotta, H. Nourzadeh, J. Sanders, D. Muller, and D. B. Ennis, ‘Highly accelerated, model‐free diffusion tensor MRI reconstruction using neural networks’, Med. Phys., vol. 46, no. 4, pp. 1581–1591, Feb. 2019.

[3] Q. Tian, B. Bilgic, Q. Fan, C. Liao, C. Ngamsombat, Y. Hu, T. Witzel, K. Setsompop, J. R. Polimeni, and S. Y. Huang, ‘DeepDTI: High-fidelity six-direction diffusion tensor imaging using deep learning’, NeuroImage, vol. 219, p. 117017, Oct. 2020.

[4] Z. Li, T. Gong, Z. Lin, H. He, Q. Tong, C. Li, Y. Sun, F. Yu, and J. Zhong, ‘Fast and Robust Diffusion Kurtosis Parametric Mapping Using a Three-Dimensional Convolutional Neural Network’, IEEE Access, vol. 7, pp. 71398–71411, 2019.

[5] D. C. Van Essen, S. M. Smith, D. M. Barch, T. E. J. Behrens, E. Yacoub, and K. Ugurbil, ‘The WU-Minn Human Connectome Project: An overview’, NeuroImage, vol. 80, pp. 62–79, Oct. 2013.

[6] S. Skare, M. Hedehus, M. E. Moseley, and T.-Q. Li, ‘Condition Number as a Measure of Noise Performance of Diffusion Tensor Data Acquisition Schemes with MRI’, Journal of Magnetic Resonance, vol. 147, no. 2, pp. 340–352, Dec. 2000.

[7] S. M. Smith, M. Jenkinson, M. W. Woolrich, C. F. Beckmann, T. E. J. Behrens, H. Johansen-Berg, P. R. Bannister, M. De Luca, I. Drobnjak, D. E. Flitney, R. K. Niazy, J. Saunders, J. Vickers, Y. Zhang, N. De Stefano, J. M. Brady, and P. M. Matthews, ‘Advances in functional and structural MR image analysis and implementation as FSL’, NeuroImage, vol. 23, pp. S208–S219, Jan. 2004

[8] D. P. Kingma, J. Ba, ‘Adam: A Method for Stochastic Optimization’, 3rd International Conference for Learning Representations, ICLR 2015 – Conference Track Proceedings, Dec. 2014

[9] C.-F. Westin, S. E. Maier, H. Mamata, A. Nabavi, F. A. Jolesz, and R. Kikinis, ‘Processing and visualization for diffusion tensor MRI’, Medical Image Analysis, vol. 6, no. 2, pp. 93–108, Jun. 2002.

Figures

Figure 1) The frobenius norm of the error map between the estimations and ground truth image. The Patch-CNN has the lowest error of any of the estimations from 6 DWI. The error is slightly higher than the error map of conventional-fitting applied to 30 DWIs.

Figure 2) Top are the FA weighted colour maps of the primary direction of diffusion. The motor tract, highlighted in yellow, is enlarged at the bottom where the primary directions of diffusion are illustrated as colour encoded sticks. The sticks are masked such that only WM voxels remain, determined by FA>0.2. Estimations from Patch-CNN are visually more similar to the GT for both RGB colourmap and sticks.

Figure 3) Scalar measure (FA and MD) estimation are shown with their corresponding difference maps. Patch-CNN estimates less grainy and more accurate images for both MD and FA when comparing against the model fit and Voxel-NN.

Figure 4) Boxplots computed over the medians of errors for each of the 4 testing subjects. For (a,c,d) the median error is computed across all of the brain voxels at each subject. For (b) median error is computed for each subject across voxels for which the primary direction of diffusion is well defined, where the linearity coefficient⁹>0.6.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

2449